電磁気の学習帳
電磁気の学習
電磁気について、基本的な知識をできるだけわかりやすくまとめていきます。
目次
電束
Q[C]の電荷から出る電束の数は誘電率εに依存しない。
電気力線
電気力線の方向は電荷+Q[C]から電荷-Q[C]へ向かう(プラスからマイナスへ向かう)。同じ電荷同士では電気力線は互いに接することはない。
- 同じ向きの電気力線同士は反発し合う。
- 電気力線は正の電荷から出て、負の電荷へ入る。
- 電気力線は、導体表面に垂直に出入りする。
- 電気力線は途中で分岐したり、相互に交差したりしない。
- 電気力線は、等電位面と直交する。
- 媒質中に置かれたQ[C]の電荷から出る電気力線の本数は、その電荷の大きさに比例し、媒質の誘電率ε[F/m]に反比例する。
- 任意の点における電気力線の密度は、その点の電界の強さを表す。
- 任意の点における電界の向きは、電気力線の接線の向きと一致する。
- 電界中に置かれた導体内部の電界の強さ(大きさ)は、その導体表面の電界の強さ(大きさ)に等しい。
- 電験3種過去問【2023年(上期)理論 問2】(静電界での電気力線と電界の強さ)
- 電験3種過去問【2020年理論 問2】(電気力線の分布)
- 電験3種過去問【2017年理論 問1】(電気力線に関する知識)
静電誘導
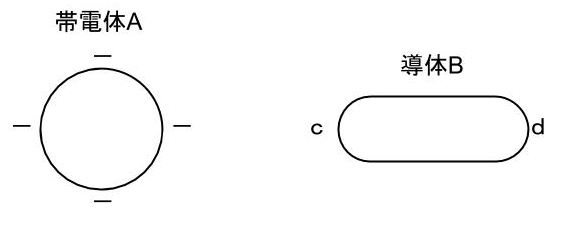
導体が帯電するとき、電荷は導体の表面にだけ分布する。導体外部には電界ができる。ただし、導体内部は等電位であり、電界は零である。
図のように真空中において、負に帯電した帯電体Aを、帯電していない絶縁された導体Bに近づけると、導体Bの帯電体Aに近い側の表面c付近に正の電荷が現れ、それと反対側の表面d付近に負の電荷が現れる。
この現象を静電誘導という。
導体Bの代わりにに絶縁体を用いて同様の現象が起こるが、これを静電分極という。静電誘導との違いは、静電誘導は導体中の自由電子の移動に伴い表面電荷が生じるのに対して、静電分極は絶縁体中の分子が静電気力の影響で、電荷の偏りが生じ、表面電荷が生じるものである。
静電遮へい
電界中に置かれた導体内部の電界の強さ(大きさ)は、零(等電位)となる。
静電遮へいは、導体で完全に囲まれた、中空部分の電界は 0 で等電位となり、導体の中空部分が外部の電場の影響を受けないことをいう。
帯電していない中空の球導体Bが設置されていないとき、帯電した導体Aを導体Bで包んだとしても、導体Bの外部に電界ができる。
平行平板コンデンサ
a 極板間の電位は、極板Aからの距離に対して比例の関係で変化する。
b 極板間の電界の強さは、極板Aからの距離に対して一定である。
c 極板間の等電位線は、極板に対して平行である。
d 極板間の電気力線は、極板に対して垂直である。
電荷、電束、電界
誘電率\(\epsilon\)の空間にQ[C]の電荷が置かれているとき、r[m]離れた点における電界E[V/m]は
\(\displaystyle E=\frac{Q}{4\pi\epsilon_0}\frac{1}{r^2}\) [V/m]
誘電率\(\epsilon\)の空間にQ[C]の電荷が置かれているとき、r[m]離れた点における電位V[V]は
\(\displaystyle V=\frac{Q}{4\pi\epsilon_0}\frac{1}{r}\) [V]
Q[C]の電荷から、Q[C]の電束が発生する。
単位面積当たりの電束を電束密度D[C/㎡]で表す。
電界の大きさをE[V/m]、誘電率をεとすると
\(D=εE\) [C/㎡]
と表される。
電界E[V/m]は、電極間距離をd[m]、電極間電位差をV[V]とすると
\(\displaystyle E=\frac{V}{d}\)
となる。
- ★電験3種過去問【2023年(前期)理論 問1】(コンデンサの電界・電荷密度・電荷)
- 電験3種過去問【2020年理論 問17】(コンデンサの絶縁破壊電界)
- 電験3種過去問【2019年理論 問1】(点電荷がつくる電位差)
- 電験3種過去問【2019年理論 問2】(コンデンサ内部の電界の強さ)
- 電験3種過去問【2016年理論 問1】(二つの点電荷がつくる等電位面分布)
- 電験3種過去問【2016年電力 問2】(平行平板コンデンサに関する知識)
- 電験3種過去問【2014年理論 問1】(コンデンサ内部の電位)
- 電験3種過去問【2013年理論 問17】(電荷を帯びた金属球による電界)
- 電験3種過去問【2012年理論 問1】(帯電コンデンサの結合)
- 電験3種過去問【2012年理論 問2】(平行平板コンデンサの誘電体)
- 電験3種過去問【2010年理論 問1】(点電荷がつくる電位)
- 電験3種過去問【2010年理論 問2】(コンデンサの内部電界と電荷)
- 電験3種過去問【2009年理論 問1】(コンデンサの電界・電束密度・電荷)
- ★電験3種過去問【2009年理論 問2】(点電荷・電極板がつくる静電界)
- 電験1種過去問【2012年理論 問1】(線電荷周囲の電界に関する記述)
- 電験1種過去問【2011年理論 問5】(静電容量と接地抵抗に関する記述)
- 電験1種過去問【2010年理論 問6】(平行平板電極と誘電体に関する記述)
コンデンサに蓄えられるエネルギー
コンデンサ全体に蓄えられる電界のエネルギーは
\(\displaystyle W=\frac{1}{2}CV^2=\frac{1}{2}QV=\frac{1}{2}\frac{Q^2}{V}\)[J]
で表される。
コンデンサの静電容量C[F]は
\(\displaystyle C=ε\frac{S}{d}\text{[F]}\)
となる。
- 電験3種過去問【2017年理論 問2】(コンデンサに蓄えられるエネルギー)
- 電験3種過去問【2015年理論 問1】(平行平板コンデンサの特性)
- 電験3種過去問【2015年理論 問2】(コンデンサに関する知識)
- 電験3種過去問【2013年理論 問1】(平行平板コンデンサに関する知識)
- 電験3種過去問【2011年理論 問2】(コンデンサの静電容量とエネルギー)
- 電験2種過去問【2019年理論 問1】(コンデンサ内の変位電流)
電界中における電荷にはたらく力
E[V/m]の電界中に、q[C]の電荷があるとき、この電荷にはたらく力F[N]は、電界の向きと同じとなり、
\(\displaystyle F=qE\text{[N]}\)
電荷q[C]にかかる、静電力Fに対して、移動した距離が、電荷の仕事となる。
仕事W[J]は、F[N]の力でd[m]移動したとすると
W=Fd[J]
上式より
W=qEd[J]
クーロンの法則
クーロンの法則より、距離r[m]離れた電荷Q1[C]及び電荷Q2[C]に互いに作用する静電力F[N]は
\(\displaystyle F=\frac{1}{4\pi ε_0 ε_s}\times \frac{Q_1 Q_2}{r^2}\text{[N]}\)
で与えられる。
- 電験3種過去問【2021年理論 問1】(平行板コンデンサの電界と電束)
- 電験3種過去問【2021年理論 問2】(小球間に作用する静電力と誘電率の関係)
- 電験3種過去問【2021年理論 問17】(コンデンサ内の電界の強さと蓄積エネルギー)
- 電験3種過去問【2018年理論 問1】(帯電導体球に働く力)
- 電験3種過去問【2018年理論 問2】(平行平板コンデンサの電界)
- 電験3種過去問【2016年理論 問8】(電気の法則に関する知識)
- 電験3種過去問【2013年理論 問2】(複数の点電荷に働く力)
磁力線
磁力線は、磁極の働きを理解するのに考えた仮想的な線である。
(1)磁力線は、磁石のN極から出てS極に入る。
(2)磁極周囲の物質の透磁率をμ[H/m]とすると、m[Wb]の磁極からm/μ本の磁力線が出入りする。
(3)磁力線の接線の向きは、その点の磁界の向きを表す。
(4)磁力線の密度は、その点の磁界の強さを表す。
(5)磁力線同士は、互いに反発し合い、交わらない。
磁束密度
磁界の強さをH[A/m]とすると
磁束は\(\Phi=\mu H\)[Wb]で与えられる。
断面積S[㎡]を貫く磁束密度は\(B=\frac{\Phi}{S}=\frac{\mu H}{S}\)[Wb/㎡]で与えられる。
磁界の強さ
点磁荷m[Wb]の磁束をもつ電磁荷から、距離r[m]離れた点の磁界の強さH[A/m]は、
\(\displaystyle H=\frac{m}{4\pi\mu_0 r^2}\)[A/m]で与えられる。
右ねじの法則
右ねじの法則に従って、導体に流れる電流の方向に対して、周囲に右回転方向の磁界を生じている。
電磁力
電流が流れている長さL[m]の直線導体を磁束密度が一様な磁界中に置くと、フレミングの左手の法則に従い、導体には電流の向きにも界磁の向きにも直角な電磁力が働く。直線導体の方向を変化させて、電流の方向が界磁の方向と同じになれば、導体に働く力の大きさは零となり、直角になれば、最大となる。力の大きさは、電流の一乗に比例する。
磁束密度B[T]の磁界に対して垂直となる方向に、長さl[m]の導体がおかれ、I[A]の電流が流れているとき、この導体にはF[N]の電磁力がはたらく。電磁力F[N]は以下となる。
F=IlB[N]
フレミングの左手の法則
均一磁界中において、磁界の方向と直角に置かれた直線状導体に直流電流を流すと、導体には電流の大きさに比例した力が働く。フレミングの左手の法則では、親指の向きが導体に働く力の向きを示す。
平行直線電流に働く力
2本の平行な直線状導体に反対向きの電流を流すと、導体には導体間距離の1乗に反比例した反発力が働く。
電流I[A]が流れる直線導体のから距離r[m]はなれた点の磁界の強さHは
H = I/(2πr)となる。この点において、もう一方の直線導体にも電流I[A]が流れているとすると、そこに働く力は
F=μHIl[N]
l[m]は導体の長さであるが、単位長さ当たりに働く力を考えるとl=1[m]となり、
F=μHIl=μI²/(2πr)[N]
つまり導体間距離の1乗に反比例した力が働く。
フレミングの右手の法則
フレミングの右手の法則は、電磁誘導による起電力の方向を覚えやすく示したもの。
人差し指を磁界の向き、親指を導体が移動する向きに向けると、中指の向きは誘導起電力の電流の向きと一致する。
長さl[m]の導線が、空間中の磁束密度B[T]なる磁界を直角に横切る方向で、速度v[m/s]で移動するとき、導線にはe[V]の誘導起電力が生じる。
このときe=Blv[V]となる。
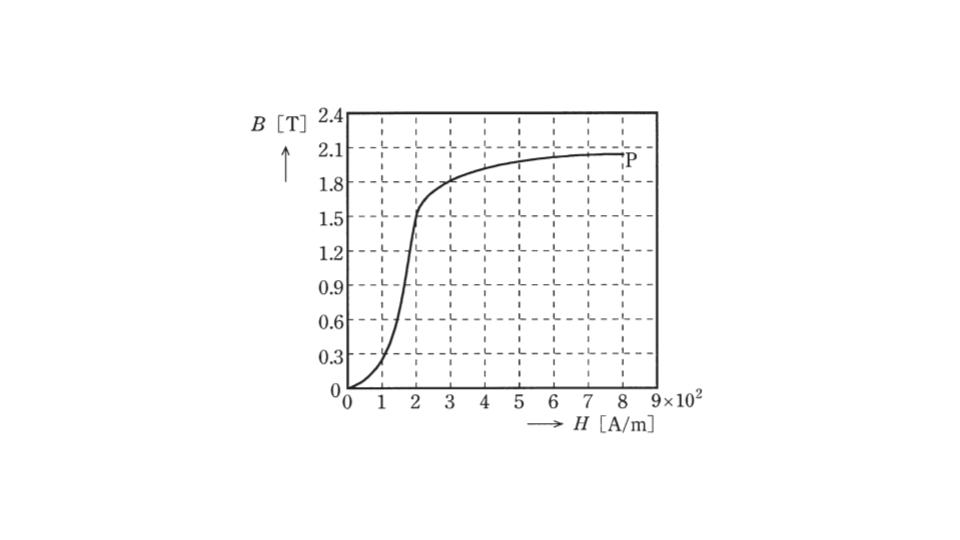
強磁性体の初期磁化特性
磁界の向きに強く磁化され、比透磁率μrが1よりも非常に大きい物質を強磁性体という。まだ磁化されていない強磁性体に磁界H[A/m]を加えて磁化していくと、磁束密度B[T]は図のように変化する。よって、透磁率μ[H/m](=B/H)も磁界の強さによって変化する。図から、この強磁性体の透磁率μの最大値は傾きが最も急峻な点である(H=2×10-2の点)。
点P以降は磁界に対する磁束密度の増加が次第に緩くなり、磁束密度はほぼ一定の値となる。この現象を磁気飽和という。
真空の透磁率をμ0=4π×10-7[H/m]とすると比透磁率μrと透磁率μの関係は、
透磁率μ=μrμ0で与えられる。
磁気遮へい
磁界中に強磁性体を置くと、周囲の磁束は、磁束が通りやすい強磁性体の内部を通るようになる。このとき、強磁性体を中空にしておくと、中空の部分には外部の磁界の影響がほとんど及ばない。このように、強磁性体でまわりを囲んで、磁界の影響が及ばないようにすることを磁気遮へいという。
ソレノイド内部の磁界
1[m]当たりの巻数がNの無限に長いソレノイドに電流I[A]を流すと、ソレノイドの内部には磁界H=NI[A/m]が生じる。磁界の大きさは、ソレノイドの寸法や内部に存在する物質の種類に影響されない。
電磁誘導
電磁誘導により、コイルに生じる誘導電流はレンツの法則により、磁束の変化を妨げる方向に発生する。
レンツの法則は、「電磁誘導によってコイルに生じる起電力は、誘導起電力によって生じる電流がコイル内の磁束の変化を妨げる向きとなるように発生する」という法則である。
コイルに生じる起電力v[V]は、コイルの巻数N、コイルを貫く磁束φ[Wb]とすると、
\(\displaystyle v=-N\frac{dφ}{dt}\)
コイルの自己インダクタンス
磁気回路(環状鉄心)の長さをl[m]、鉄心の断面積をS[m²]、コイルの巻数をN[回]、鉄心の透磁率をμとすると、自己インダクタンスL[H]は次式で与えられる。
L=μN²S/l[H]
従って、巻数Nの2乗に比例し、磁路の長さlに反比例する。
自己インダクタンスLのN巻コイルにIの電流を流すとき、磁束φ[Wb]と磁束鎖交数Φ[Wb]は次式となる。
\(\displaystyle \phi=N \varphi=LI\) [Wb]
コイルに電流Iを流すと、コイルに発生する磁束鎖交数ΦはIに比例する。このときの比例定数L[H]を自己インダクタンスという。
コイルに蓄えられるエネルギーW[J]は
\(\displaystyle W=\frac{1}{2}LI^2\) [J]
コイルの相互インダクタンス
相互インダクタンスM=k√(L₁L₂)[H]であたえられ、漏れ磁束の程度である結合係数kは0~1となる。
和動結合のとき、合成インダクタンスL=L₁+L₂+2M[H]差動結合のとき、合成インダクタンスL=L₁+L₂-2M[H]和動結合のときは、それぞれの自己インダクタンスの合計値よりも大きくなる。
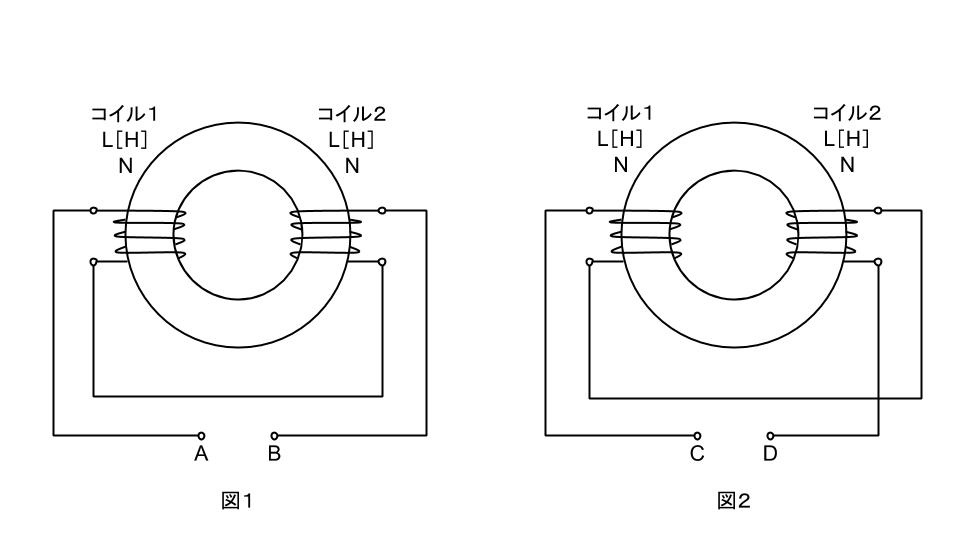
1次コイルL1[H]と2次コイルL2[H]がつくる磁界が、磁気的に接続され、同じ大きさの電流が流れるように接続されているとき、磁界の向きが同じになる接続方法を和動接続という。この時の、合成インダクタンスの値LS[H]は、1次コイルL1[H]と2次コイルL2[H]がそれぞれつくる相互インダクタンスをM[H]とすると、
LS=L1+L2+2M[H]
また、磁界の向きが逆になるような接続方法を差動接続という。この時の、合成インダクタンスの値LD[H]は、
LD=L1+L2-2M[H]
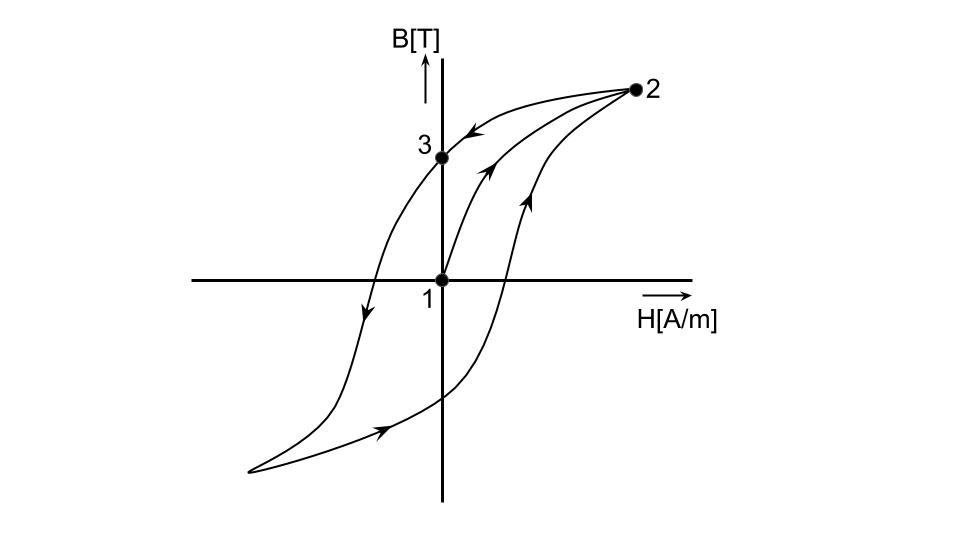
ヒステリシスループ
積層した電磁鋼板の鉄心などの強磁性体に一様な交番磁界を印加すると、強磁性体内の磁束密度B[T]は磁界H[A/m]に比例せず、定常状態において図に示すような時計回りの軌跡を描く。これを磁化特性(ヒステリシスループ)と呼ぶ。
図中の横軸は磁界の強さH[A/m]、縦軸は磁束密度B[T]を表す。
図中のBr[T]は、残留磁束密度(残留磁気)と呼ばれ、Hc[A/m]は保磁力と呼ばれる。
強磁性体を永久磁石として用いる場合、Br[T]とHc[A/m]の両方が大きい材料すなわち、残留磁気と保磁力が大きい材料が望ましい。
ヒステリシス曲線に囲まれる面積は熱として失われるエネルギーとなる。
この特性により生じる損失をヒステリシス損と呼び、それは印加する交番磁界の周波数に比例する。ヒステリシスループで囲まれた部分の面積S[J/m3]は、交番磁界1周期における強磁性体内で消費される単位体積当たりのエネルギーを表す。ここで、体積1.5×10-3m3の強磁性体に60Hzの一様な交番磁界を与えたところ、S=5.0×102J/m3であったとする。このときのヒステリシス損は45Wである。
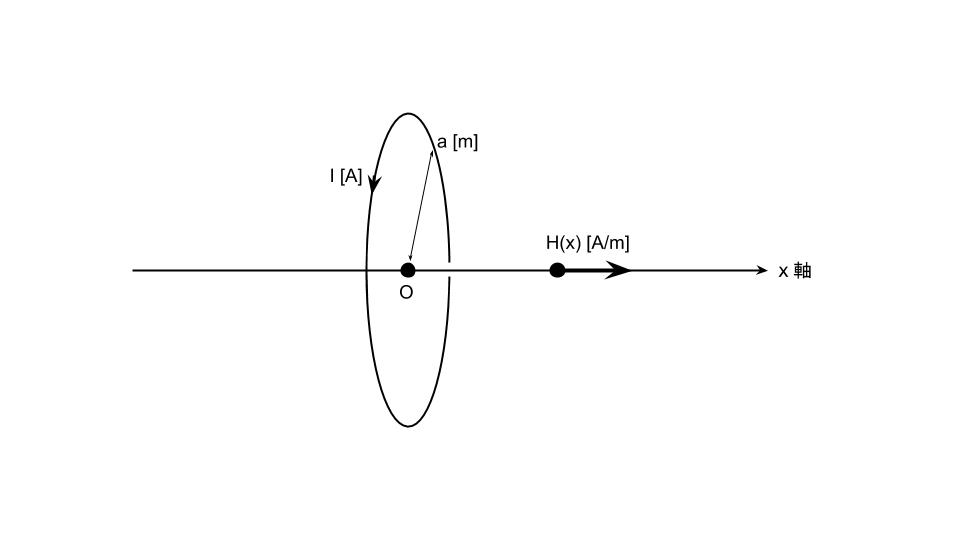
円電流がつくる磁界の強さ
アンペアの右ねじの法則に従って、電流I[A]によって図のx方向にH(x)[A/m]が生じる。このときの、中心の磁界の強さH(0)[A/m]は、ビオ・サバールの法則より求めることができる。
\(\displaystyle H(0)=\frac{I}{2a}\)[A/m]
- 電験3種過去問【2018年理論 問4】(円電流がつくる磁界の強さ)
- 電験3種過去問【2016年理論 問3】(円電流がつくる磁界の強さ)
- 電験3種過去問【2009年理論 問4】(円形電流が中心につくる磁界)
無限長線状電流による磁界(磁場に関するアンペールの法則)
無限に長い導線に電流I[A]がながれているとき、導線から垂直距離でa[m]離れている点Pの磁界の強さH[A/m]は以下となる。
\(\displaystyle H= \frac{I}{2 \pi a}\text{[A/m]}\)
- 電験3種過去問【2014年理論 問4】(直線電流がつくる磁界が打ち消し合う点)
- 電験3種過去問【2013年理論 問4】(線導体に生じる力)
- 電験3種過去問【2012年理論 問4】(無限長直線導体に働く力)
有限長線状電流による磁界
磁気回路
環状鉄心に絶縁電線を巻いて作った磁気回路には、磁気抵抗がある。
- 磁気抵抗は、磁束の通りにくさを表し、次の式で表される。
磁気抵抗=\(\displaystyle\frac{起磁力}{磁束}\) - 磁気抵抗は、磁路の断面積に反比例する。
- 磁気抵抗は、比透磁率に反比例する。
- 磁気抵抗は、磁路の長さに比例する。
- 磁気抵抗の単位は、毎ヘンリー[ H⁻¹ ]である。
磁気回路は、電気回路におけるオームの法則のように扱うことができる。
- 電気抵抗が導体断面積に反比例するように、磁気抵抗は、鉄心断面積に反比例する。
- 鉄心の透磁率が大きいほど、磁気抵抗は小さくなる。
- 起磁力が同じ場合、鉄心の磁気抵抗が大きいほど、鉄心を通る磁束は小さくなる。
- 磁気回路における起磁力と磁気抵抗は、電気回路におけるオームの法則の起電力と電気抵抗にそれぞれ対応する。また、透磁率は電気回路の導電率に、磁束は電気回路の電流にそれぞれ対応する。
起磁力
\(\displaystyle F=NI\)[A]
(N:巻数、I:電流[A])
磁気抵抗
\(\displaystyle R=\frac{l}{\mu S}\)[A/Wb]または[ H⁻¹ ]
(μ:透磁率、l:磁路の長さ[m]、S:磁路の断面積[m²])
磁気回路中の磁束
\(\displaystyle \phi=\frac{F}{R}\)[Wb]
磁束密度
\(\displaystyle B=\frac{\phi}{S}\)[Wb/m²]\(\displaystyle =\frac{\phi}{S}\)[T]

ディスカッション
コメント一覧
まだ、コメントがありません