電験3種過去問【2012年理論 問2】
【電磁気】平行平板コンデンサの誘電体《正誤問題》
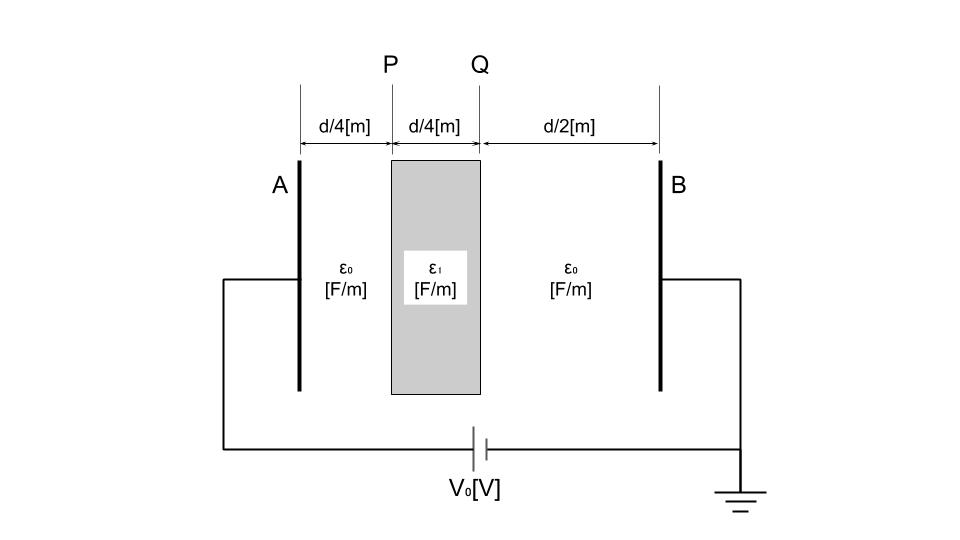
極板A-B間が誘電率ε0[F/m]の空気で満たされている平行平板コンデンサの空気ギャップ長をd[m]、静電容量をC0[F]とし、極板間の直流電圧をV0[V]とする。極板と同じ形状と面積を持ち、厚さがd/4[m]、誘電率ε1[F/m]の個体誘電体(ε1>ε0)を図に示す位置P-Q間に極板と平行に挿入すると、コンデンサ内の電位分布は変化し、静電容量はC1[F]に変化した。このとき、誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし、空気の誘電率をε0、コンデンサの端効果は無視できるものとし、直流電圧V0[V]は一定とする。
(1)位置Pの電位は、個体誘電体を挿入する前の値よりも低下する。
(2)位置Qの電位は、個体誘電体を挿入する前の値よりも上昇する。
(3)静電容量C1[F]は、C0[F]よりも大きくなる。
(4)個体誘電体を導体に変えた場合、位置Pの電位は個体誘電体又は導体を挿入する前の値よりも上昇する。
(5)個体誘電体を導体に変えた場合の静電容量C2[F]は、C0[F]よりも大きくなる。

 https://archivelog.net/denken/
https://archivelog.net/denken/
ディスカッション
コメント一覧
まだ、コメントがありません