電験３種過去問【2010年理論 問2】
【電磁気】コンデンサの内部電界と電荷《計算問題》
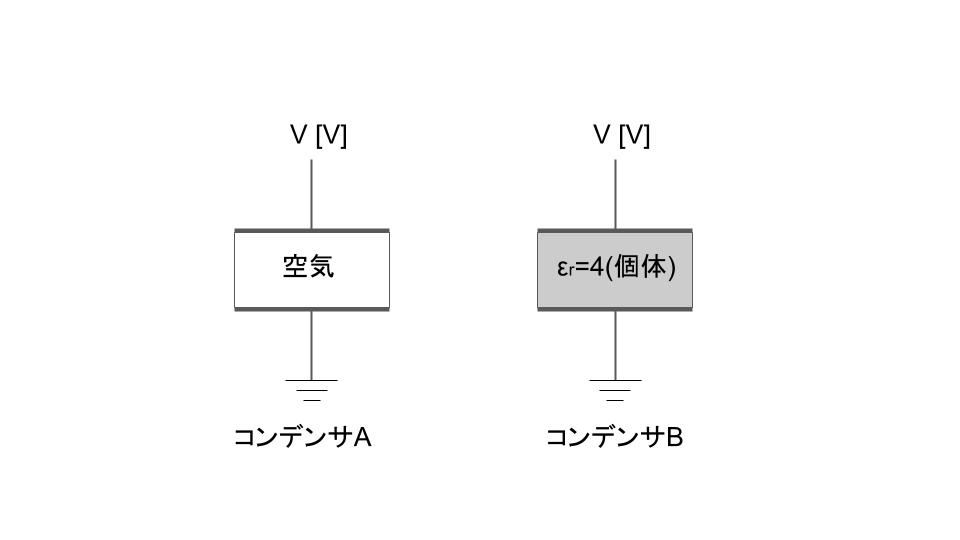
図に示すように、電極板面積と電極板間隔がそれぞれ同一の２種類の平行平板コンデンサがあり、一方を空気コンデンサA、他方を個体誘電体（比誘電率εr＝４）が満たされたコンデンサBとする。両コンデンサにおいて、それぞれ一方の電極に直流電圧V[V]を加え、他方の電極を接地したとき、コンデンサBの内部電界[V/m]及び電極板上に蓄えられた電荷[C]はコンデンサAのそれぞれ何倍となるか。その倍率として、正しいものを組み合わせたのは次のうちどれか。
ただし、空気の比誘電率を１とし、コンデンサの端効果は無視できるものとする。
| 内部電界 | 電荷 | |
| （１） | 1 | 4 |
| （２） | 4 | 4 |
| （３） | 1/4 | 4 |
| （４） | 4 | 1 |
| （５） | 1 | 1 |
https://archivelog.net/denken3-kakomon/
https://archivelog.net/denken/