電験１種過去問【2009年理論 問1】

解答

解説

　次の文章は、２本の導線ようり成る平行往復回路の外部自己インダクタンスに関する記述である。文中の\(\fbox{空所欄}\)に当てはまる式又は語句を解答群の中から選べ。なお、空気の透磁率を\(\mu_0\)とする。
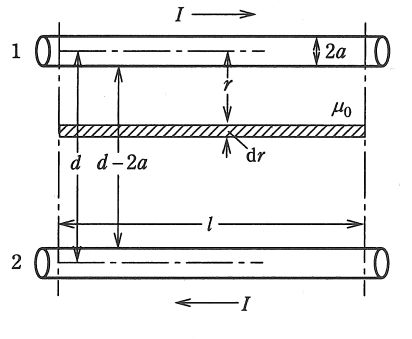
　図のように、半径がａで、無限に長い２本の導線が線間距離ｄを隔てて構成される一つの平行往復回路がある。ただし、ａ≪ｄとする。このとき、導線外部の磁束による自己インダクタンスは次のように求めることができる。
　ａ≪ｄであるから、電流は導線の中心軸に集中しているとしてよい。したがって、導線１の電流Ｉによる導体外の磁界は、ｒをその中心軸からの距離とすれば、ｒ＞ａとして、\(\displaystyle\frac{I}{2\pi r}\)となる。

磁場に関するアンペールの法則

無限に長い導線に電流I[A]がながれているとき、導線から垂直距離でa[m]離れている点Pの磁界の強さH[A/m]は以下となる。

\(\displaystyle H= \frac{I}{2 \pi a}\text{[A/m]}\)

そこで、中心軸からｒのところにあって、幅がdr、長さがｌの帯状面積 ldr を貫く磁束dφは\(\displaystyle\frac{\mu_0 I}{2\pi r}ldr\)となる。

磁束密度

磁界の強さをH[A/m]とすると
磁束は\(\Phi=\mu H\)[Wb]で与えられる。
断面積S[㎡]を貫く磁束密度は\(B=\frac{\Phi}{S}=\frac{\mu H}{S}\)[Wb/㎡]で与えられる。

　平行往復回路の外部自己インダクタンスは２本の導線間を通過している磁束から計算できる。したがって、導線１の電流Ｉによる長さｌの部分に関係する外部磁束Φはdφをｒについて\(aからd-a\)まで積分すれば、ａ≪ｄとして\(\displaystyle\Phi=\frac{\mu_0 lI}{2\pi}log_e\frac{d}{a}\)となる。

\(\displaystyle \Phi=\int d\phi\)
\(\displaystyle =\int_a^{d-a}\frac{\mu_0 I}{2\pi r}ldr\)
\(\displaystyle =\frac{\mu_0 lI}{2\pi}\int_a^{d-a}\frac{1}{r}dr\)
\(\displaystyle =\frac{\mu_0 lI}{2\pi}[log_e|r|]_a^{d-a}\)
\(\displaystyle =\frac{\mu_0 lI}{2\pi}log_e\frac{d-a}{a}\)
\(\displaystyle =\frac{\mu_0 lI}{2\pi}log_e\frac{d}{a}(∵a<<d)\)

同じく導線２の電流Ｉによる長さｌの部分に関係する外部磁束も\(\displaystyle\Phi=\frac{\mu_0 lI}{2\pi}log_e\frac{d}{a}\)と大きさも方向も全く相等しいことに注意すれば、結局、求める外部磁束は\(\displaystyle\Phi=\frac{\mu_0 lI}{2\pi}log_e\frac{d}{a}\)の２倍となる。
　したがって、無限に長い２本の平行往復回路の長さｌについての導線外部の磁束による導線外部自己インダクタンスは\(\displaystyle L=\frac{2\Phi}{I}=\frac{\mu_0 l}{\pi}log_e\frac{d}{a}\)となる。

自己インダクタンスLのコイルにIの電流を流すとき、磁束鎖交数Φ[Wb]は次式となる。

\(\displaystyle \Phi=LI\) [Wb]