電験3種過去問【2018年理論 問3】
【電磁気】点磁荷がつくる磁界の強さ《計算問題》
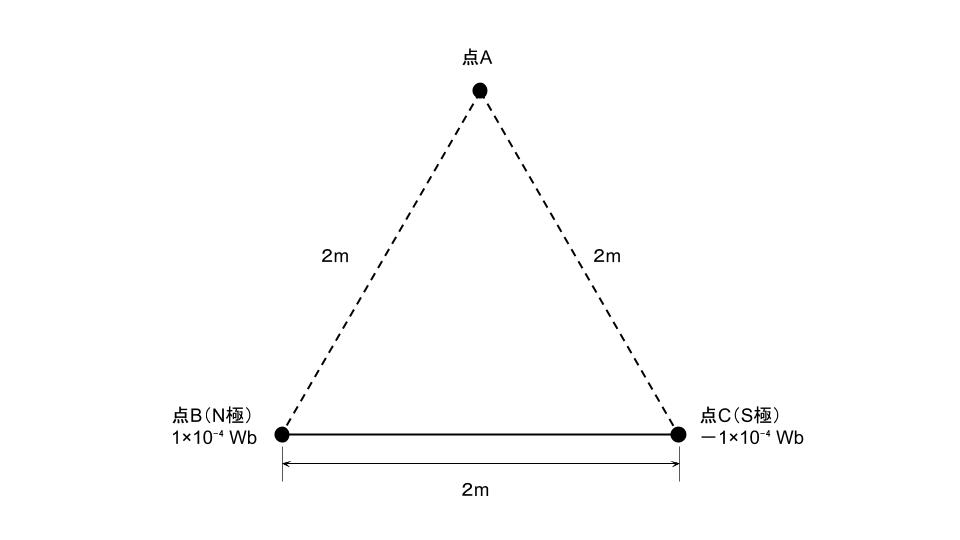
長さ2mの直線状の棒磁石があり、その両端の磁極は点磁荷とみなすことができ、その強さは、N極が1×10-4Wb、S極が-1×10-4Wbである。図のように、この棒磁石を点BC間に置いた。このとき、点Aの磁界の大きさの値[A/m]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、点A、B、Cは、一辺を2mとする正三角形の各頂点に位置し、真空中にあるものとする。真空の透磁率はμ0=4π×10-7H/mとする。また、N極、S極の各点磁荷以外の部分から点Aへの影響はないものとする。
| (1)0 | (2)0.79 | (3)1.05 | (4)1.58 | (5)3.16 |

ディスカッション
コメント一覧
まだ、コメントがありません