電験3種過去問【2009年理論 問4】
【電磁気】円形電流が中心につくる磁界《計算問題》
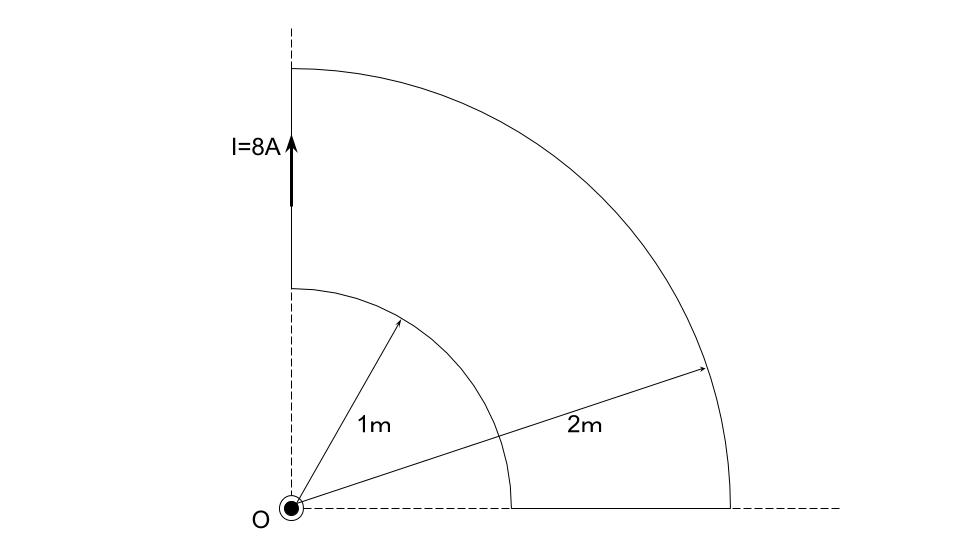
図のように、点Oを中心とするそれぞれ半径1[m]と半径2[m]の円形導線の1/4と、それらを連結する直線状の導線からなる扇形導線がある。この導線に、図に示す向きに直流電流I=8[A]を流した場合、点Oにおける磁界[A/m]の大きさとして、正しいのは次のうちどれか。
ただし、扇形導線は同一平面状にあり、その巻数は一巻である。
| (1) | 0.25 | (2) | 0.5 | (3) | 0.75 | (4) | 1.0 | (5) | 2.0 |

 https://archivelog.net/denken/
https://archivelog.net/denken/
ディスカッション
コメント一覧
まだ、コメントがありません