// google adsence用 電験３種過去問【2011年理論 問4】 | 電気主任技術者のいろは

電験３種過去問【2011年理論 問4】

2022年4月24日

【電磁気】電流がつくる磁界の大きさ《計算問題》

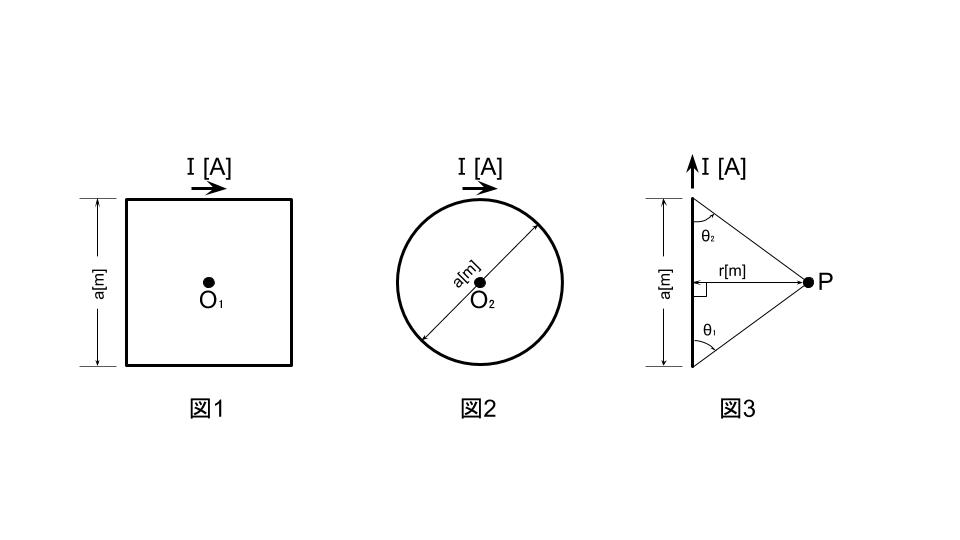
　図１のように、１辺の長さがa[m]の正方形のコイル（巻数：1）に直流電流I[A]が流れているときの中心点O1の磁界の大きさをH1[A/m]とする。また、図２のように、直径a[m]の円形コイル（巻数：1）に直流電流I[A]が流れているときの中心点O2の磁界の大きさをH2[A/m]とする。このとき、磁界の大きさの比H1/H2の値として、最も近いものを次の（１）～（５）のうちから一つ選べ。
　ただし、中心点O1、O2はそれぞれ正方形のコイル、円形のコイルと同一平面上にあるものとする。
　参考までに、図３のように、長さa[ｍ]の直線導体に直流電流I[A]が流れているとき、導体から距離r[m]離れた点Pにおける磁界の大きさH[A/m]は、H=I/(4πr)×(cosθ1+cosθ2)で求められる（角度θ1とθ2の定義は図参照）。

（１）0.45 （２）0.90 （３）1.00 （４）1.11 （５）2.22
解答と解説はこちら

解答

（２）

解説

　図１について、正方形の一辺a[m]分の線電流がO1につくる磁界の強さをH1a[A/m]とすると、図３を参考にして、
　H1a＝I/(4πr)×(cosθ1+cosθ2)
　　　＝I/{4π(a/2)}×(cos45°+cos45°)
　　　＝I/(2πa)×(1/√2+1/√2)
　　　＝I/(2πa)×(2/√2)＝I/(πa√2)

　正方形の４辺を合わせたものがH1であるので
　H1＝4H1a=4I/(πa√2)

　図２について、直径a[m]の円電流I[A]が中心につくる磁界の強さは次式で与えられる。
　H2＝I/a

　題意より、磁界の大きさの比H1/H2の値は
　H1/H2={4I/(πa√2)}/{I/a}=4/(π√2)=0.90

<<前問　　次問>>

 

電験３種過去問理論過去問, 電験3種, 理論, 電磁気, 2011年

Posted by ちゅん