電験３種過去問【2009年理論 問1】
【電磁気】ｺﾝﾃﾞﾝｻの電界・電束密度・電荷《空所問題》
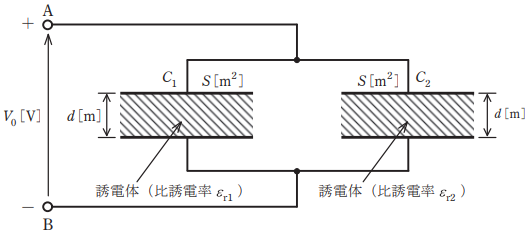
電極板面積と電極板感覚が共にS〔ｍ2〕とｄ〔ｍ〕で、一方は比誘電率がεr1の誘電体からなる平行平板コンデンサC1と、他方は比誘電率がεr2の誘電体からなる平行平板コンデンサC2がある。いま、これらを図のように並列に接続し、端子A,B間に直流電圧V0〔V〕を加えた。このとき、コンデンサC1の電極板間の電界の強さをE1〔V/m〕、電束密度をD1〔C/ｍ2〕、また、コンデンサC2の電極板間の電界の強さE1〔V/m〕、電束密度をD2〔C/m²〕とする。両コンデンサの電界の強さE1〔V/m〕とE2〔V/m〕はそれぞれ【（ア）】であり、電束密度D1〔C/m2〕と電束密度D2〔C/m2〕はそれぞれ【（イ）】である。したがって、コンデンサC1に蓄えられる電荷をQ1〔C〕、コンデンサC2に蓄えられる電荷をQ2〔C〕とすると、それらはそれぞれ【（ウ）】となる。
ただし、電極板の厚さ及びコンデンサの端効果は、無視できるものとする。また、真空の誘電率をε0〔F/m〕とする。
上記の記述中の空白個所（ア）、（イ）及び（ウ）に当てはまる式として、正しいものを組み合わせたのは次のうちどれか。
| （ア） | （イ） | （ウ） | |
| （１） | E1=(εr₁／d)V₀ E2=(εr₂／d)V₀ |
D1=(εr₁／d)SV₀ D2=(εr₂／d)SV₀ |
Q1={(ε₀εr₁)／d}SV₀ Q2={(ε₀εr₂)／d}SV₀ |
| （２） | E1=(εr₁／d)V₀ E2=(εr₂／d)V₀ |
D1={(ε₀εr₁)／d}V₀ D2={(ε₀εr₂)／d}V₀ |
Q1={(ε₀εr₁)／d}SV₀ Q2={(ε₀εr₂)／d}SV₀ |
| （３） | E1=V₀／d E2=V₀／d |
D1={(ε₀εr₁)／d}SV₀ D2={(ε₀εr₂)／d}SV₀ |
Q1={(ε₀εr₁)／d}V₀ Q2={(ε₀εr₂)／d}V₀ |
| （４） | E1=V₀／d E2=V₀／d |
D1={(ε₀εr₁)／d}V₀ D2={(ε₀εr₂)／d}V₀ |
Q1={(ε₀εr₁)／d}SV₀ Q2={(ε₀εr₂)／d}SV₀ |
| （５） | E1={(ε₀εr₁)／d}SV₀ E2={(ε₀εr₂)／d}SV₀ |
D1={(ε₀εr₁)／d}V₀ D2={(ε₀εr₂)／d}V₀ |
Q1=(ε₀／d)SV₀ Q2=(ε₀／d)SV₀ |
https://archivelog.net/denken3-kakomon/
https://archivelog.net/denken/