電験３種過去問【2016年理論 問1】
【電磁気】二つの点電荷がつくる等電位面分布《計算問題》
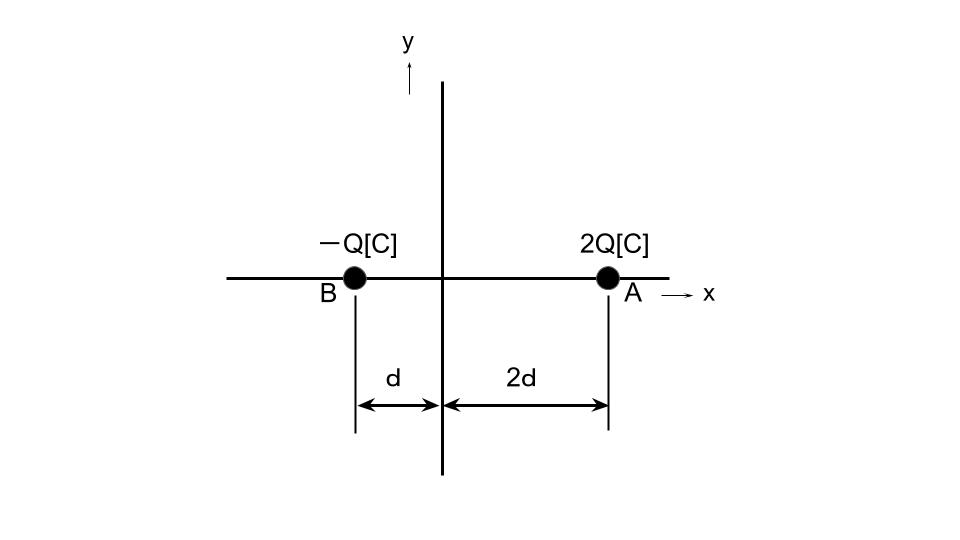
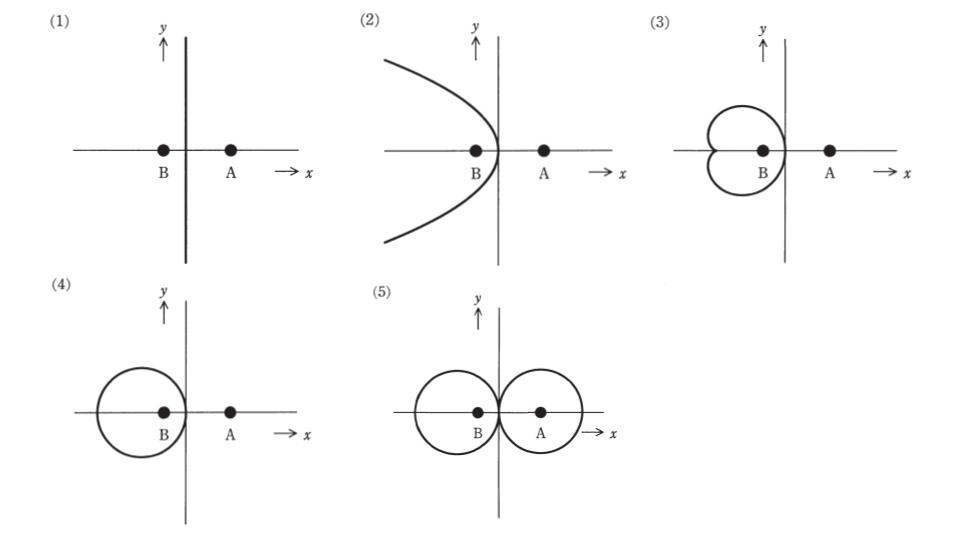
真空中において、図のようにｘ軸上で距離3ｄ[ｍ]隔てた点A(2d,0)、点B(-d,0)にそれぞれ2Q[C]、－Q[C]の点電荷が置かれている。 ｘｙ平面上で電位が０Vとなる等電位線を表す図として、最も近いものを次の（１）～（５）のうちから一つ選べ。
電験、電気その他のことをアーカイブするブログ
2022年11月29日
真空中において、図のようにｘ軸上で距離3ｄ[ｍ]隔てた点A(2d,0)、点B(-d,0)にそれぞれ2Q[C]、－Q[C]の点電荷が置かれている。 ｘｙ平面上で電位が０Vとなる等電位線を表す図として、最も近いものを次の（１）～（５）のうちから一つ選べ。
（４）
真空中に置かれた点電荷Q[C]が、r[ｍ]はなれた点につくる電位V[V]は、真空の誘電率を\(\epsilon_0\)とすると
\(\displaystyle V=\frac{Q}{4\pi\epsilon_0}\frac{1}{r}\) [V]
で与えられる。
いま、点Aに置かれた電荷2Q[C]がつくる電位VA[V]はｘｙ平面上に、次式で与えられる。
\(\displaystyle V_A=\frac{2Q}{4\pi\epsilon_0}\frac{1}{\sqrt{(x-2d)^2+y^2}}\) [V]
また、点Bに置かれた電荷-Q[C]がつくる電位VB[V]はｘｙ平面上に、次式で与えられる。
\(\displaystyle V_B=\frac{-Q}{4\pi\epsilon_0}\frac{1}{\sqrt{(x+d)^2+y^2}}\) [V]
題意より、VA+VB＝0となる条件は、
\(\displaystyle \frac{2Q}{4\pi\epsilon_0}\frac{1}{\sqrt{(x-2d)^2+y^2}}-\frac{Q}{4\pi\epsilon_0}\frac{1}{\sqrt{(x+d)^2+y^2}}=0\)
\(\displaystyle \frac{2Q}{4\pi\epsilon_0}\frac{1}{\sqrt{(x-2d)^2+y^2}}=\frac{Q}{4\pi\epsilon_0}\frac{1}{\sqrt{(x+d)^2+y^2}}\)
\(\displaystyle \frac{2}{\sqrt{(x-2d)^2+y^2}}=\frac{1}{\sqrt{(x+d)^2+y^2}}\)
\(\displaystyle \frac{4}{(x-2d)^2+y^2}=\frac{1}{(x+d)^2+y^2}\)
\(\displaystyle 4(x+d)^2+4y^2=(x-2d)^2+y^2\)
\(\displaystyle 4x^2+8dx+4d^2+4y^2=x^2-4dx+4d^2+y^2\)
\(\displaystyle 3x^2+12dx+3y^2=0\)
\(\displaystyle x^2+4dx+y^2=0\)
\(\displaystyle (x+2d)^2-4d^2+y^2=0\)
\(\displaystyle (x+2d)^2+y^2=(2d)^2\)
つまり、中心が（-2d,0）で半径が2ｄの円グラフとなる。（４）が正しい。
