電験3種過去問【2017年理論 問3】
【電磁気】コイルの相互インダクタンス《計算問題》
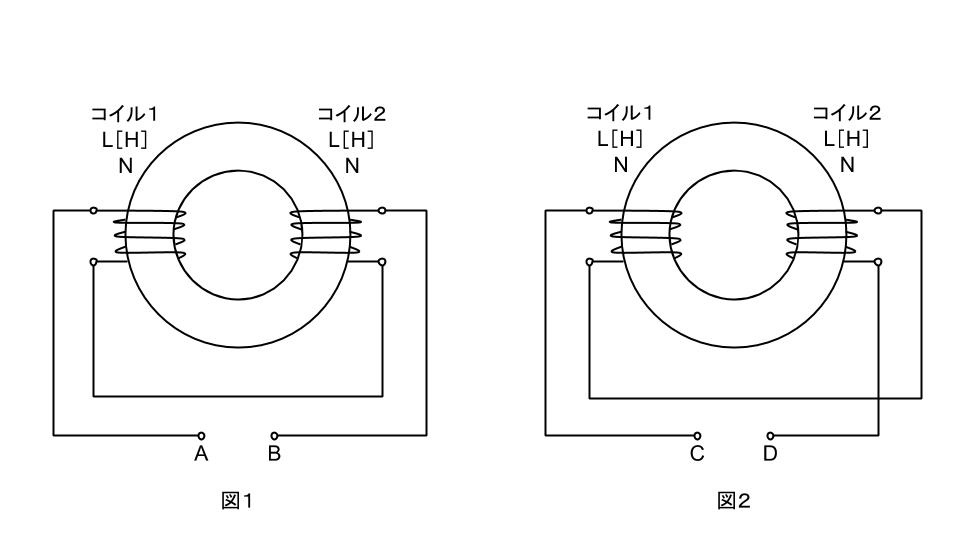
環状鉄心に、コイル1及びコイル2が巻かれている。二つのコイルを図1のように接続したとき、端子A-B間の合成インダクタンスの値は1.2Hであった。次に図2のように接続したとき、端子C-D間の合成インダクタンスの値は2.0Hであった。このことから、コイル1の自己インダクタンスLの値[H]、コイル1及びコイル2の相互インダクタンスMの値[H]の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、コイル1及びコイル2の自己インダクタンスはともにL[H]、その巻数をNとし、また、鉄心は等断面、等質であるとする。
| 自己インダクタンスL | 相互インダクタンスM | |
| (1) | 0.4 | 0.2 |
| (2) | 0.8 | 0.2 |
| (3) | 0.8 | 0.4 |
| (4) | 1.6 | 0.2 |
| (5) | 1.6 | 0.4 |

 https://archivelog.net/denken/
https://archivelog.net/denken/
ディスカッション
コメント一覧
まだ、コメントがありません