// google adsence用 電験３種過去問【2010年理論 問3】 | 電気主任技術者のいろは

電験３種過去問【2010年理論 問3】

2022年4月24日

【電磁気】導体棒に発生する誘導起電力《計算問題》

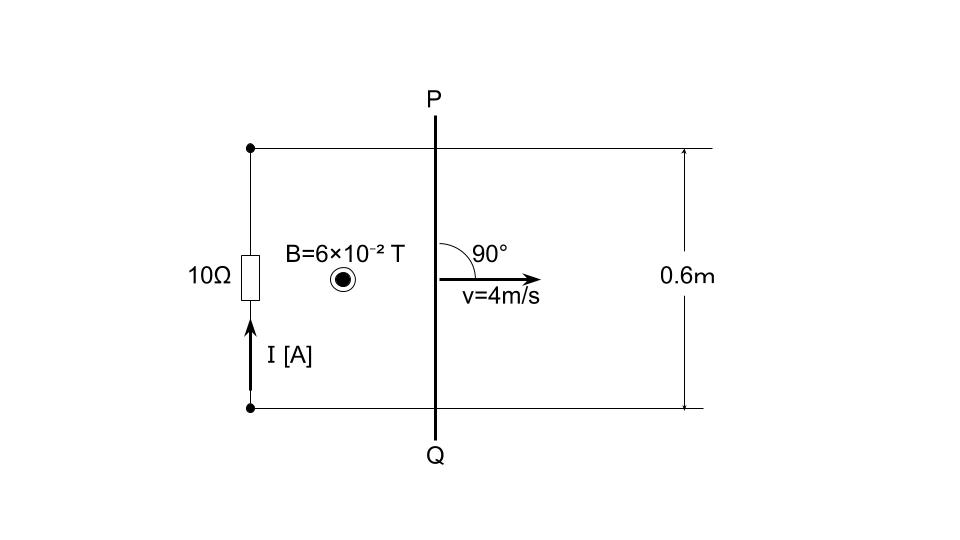
　紙面に平行な水平面内において、0.6[ｍ]の間隔で張られた２本の直線状の平行導線に10[Ω]の抵抗が接続されている。この平行導線に垂直に、図に示すように、直線状の導体棒PQを渡し、紙面の裏側から表側に向かって磁束密度B=6×10-2[T]の一様な磁界をかける。ここで、導体棒PQを磁界と導体棒に共に垂直な矢印の方向に一定の速さｖ＝4[m/s]で平行導線上を移動させているときに、10[Ω]の抵抗に流れる電流I[A]の値として、正しいのは次のうちどれか。
　ただし、電流の向きは図に示す矢印の向きを正とする。また、導線及び導体棒PQの抵抗、並びに導線と導体棒との接触抵抗は無視できるものとする。

（１）-0.0278 （２）-0.0134 （３）-0.0072 （４）0.0144 （５）0.0288
解答と解説はこちら

解答

（４）

解説

　長さｌ[ｍ]の導線が、空間中の磁束密度B[T]なる磁界を直角に横切る方向で、速度ｖ[m/s]で移動するとき、導線にはe[V]の誘導起電力が生じる。
　このときe=Blv[V]となる。

　問題中では、長さ0.6[ｍ]の導体棒が、空間中の磁束密度6×10-2[T]なる磁界を直角に横切る方向で、4[m/s]で移動している。このとき導体棒に生じる誘導起電力e[V]は
　e=Blv=6×10-2×0.6×4＝14.4×10-2[V]

従って、10[Ω]の抵抗に流れる電流I[A]は
　I＝e/10=14.4×10-2/10＝0.0144[A]

なお、電流の流れる方向は、フレミングの右手の法則に従って、正の方向となる。

<<前問　　次問>>

 

電験３種過去問理論過去問, 電験3種, 理論, 電磁気, 2010年

Posted by ちゅん