電験３種過去問【2017年理論 問2】

解答

（２）

解説

　コンデンサに蓄えられるエネルギーW＝(1/2)CV²＝(1/2)Q²/C[J]で与えられる。（Cはコンデンサの静電容量、Vはコンデンサに掛かる電圧、Qはコンデンサに蓄えられる電荷）

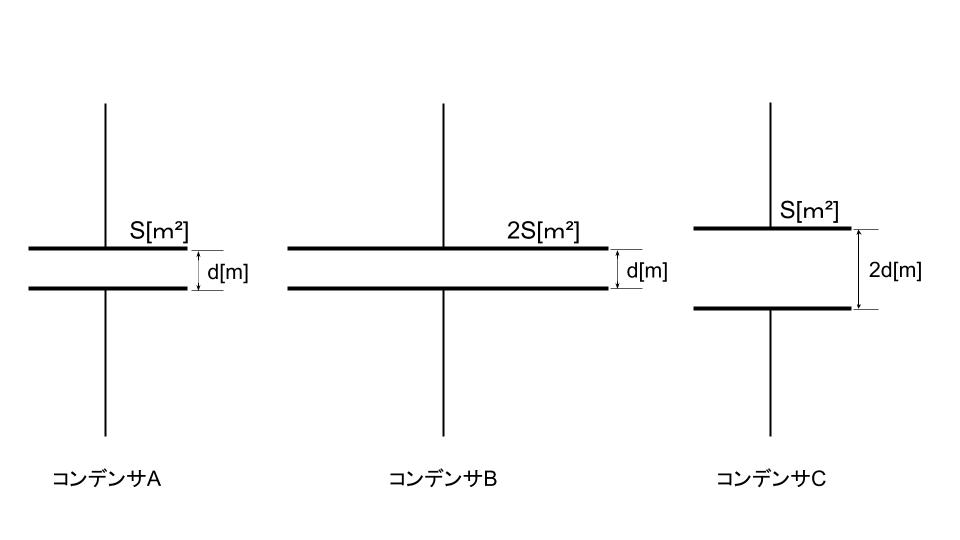
　問題中の条件では、コンデンサ極板間の電界の強さE＝V/d[V/m]（Vはコンデンサに掛かる電圧[V]、dはコンデンサの極板間隔[ｍ]）は全て等しい。コンデンサAに掛かる電圧をV_A[V]、コンデンサBに掛かる電圧をV_B[V]、コンデンサCに掛かる電圧をV_C[V]とすると、

　E=V_A/d＝V_B/d＝V_C/(2d)

　すなわち、V_A＝V_B、V_C＝2V_A＝2V_Bの関係が成り立つ。

　コンデンサの静電容量C＝εS/d[F]（εはコンデンサ極板間の誘電率[F/m]、Sはコンデンサの極板面積[ｍ²]、dはコンデンサの極板間隔[ｍ]）で与えられる。コンデンサAの静電容量をC_A[F]、コンデンサBの静電容量をC_B[F]、コンデンサCの静電容量をC_C[F]とすると、

　C_A＝εS/d[F]

　C_B＝ε2S/d＝2C_A[F]

　C_C＝εS/(2d)＝C_A/2[F]

　コンデンサAに蓄えられるエネルギーをW_A[J]、コンデンサBに蓄えられるエネルギーをW_B[J]、コンデンサCに蓄えられるエネルギーをW_C[J]とすると、

　W_A＝(1/2)C_AV_A²[J]

　W_B＝(1/2)C_BV_B²＝(1/2)2C_AV_A²＝2W_A[J]

　W_C＝(1/2)C_CV_C²＝(1/2)(C_A/2)(2V_A)²＝2W_A[J]

　すなわち、コンデンサ接続前に、各コンデンサに蓄えられるエネルギーの総和W_E[J]は

　W_E＝W_A+W_B+W_C＝W_A+2W_A+2W_A＝5W_A[J]

　接続前に、コンデンサAに蓄えられた電荷をQ_A[C]、コンデンサBに蓄えられた電荷をQ_B[C]、コンデンサCに蓄えられた電荷をQ_C[C]とすると、

　Q_A＝C_AV_A＝εSV_A/d[C]

　Q_B＝C_BV_B＝2εSV_A/d＝2Q_A[C]

　Q_C＝C_CV_C＝εS2V_A/(2d)＝εSV_A/d＝Q_A[C]

　コンデンサA、B、Cを同一極性で並列接続したときの電荷の総和と、各コンデンサに蓄えられた電荷の総和は等しく、電荷の総和Q_P[C]は

　Q_P＝Q_A+Q_B+Q_C＝Q_A+2Q_A+Q_A＝4Q_A[C]

　コンデンサA、B、Cを並列接続したときの、合成静電容量C_P[F]は各コンデンサの静電容量の総和であるので、

　C_P＝C_A+C_B+C_C＝C_A+2C_A+C_A/2＝7C_A/2[F]

　並列接続後の合成静電容量C_P[F]のコンデンサに蓄えられるエネルギーW_P[J]は

　W_P＝(1/2)Q_P²/C_P＝(1/2)(4Q_A)²/(7C_A/2)＝16Q_A²/(7C_A)=32/7×(1/2)Q_A²/C_A[J]

　W_A＝(1/2)Q_A²/C_Aであるので、

　W_P=32/7×W_A[J]

　題意より、求めるエネルギー比は

　W_P/W_E＝(32/7×W_A)/5W_A＝32/35＝0.91となる。