電験３種過去問【2015年理論 問2】
【電磁気】コンデンサに関する知識《空所問題》
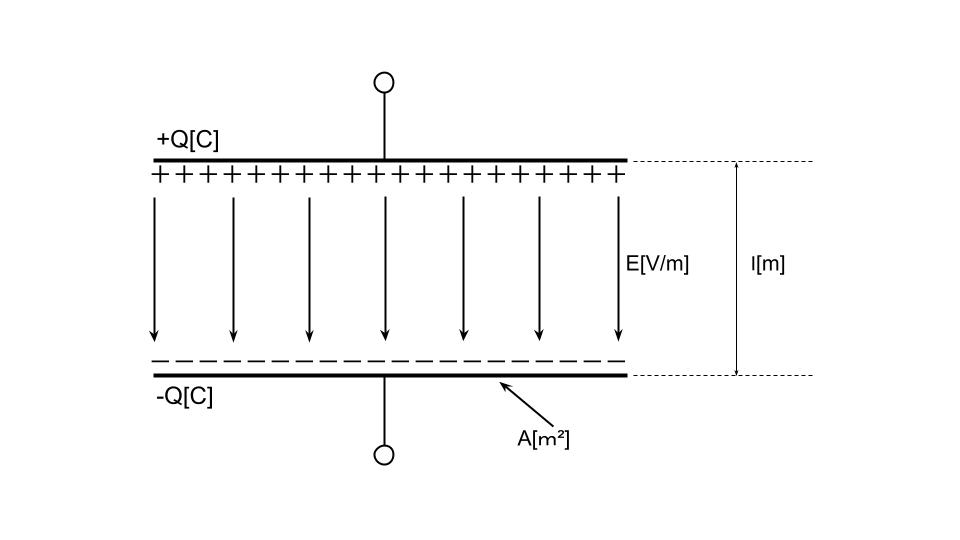
図のように、真空中で２枚の電極を平行に向かい合せたコンデンサを考える。各電極の面積をA[m2]、電極の間隔をｌ[ｍ]とし、端効果を無視すると、静電容量は【（ア）】[F]である。このコンデンサに直流電圧源を接続し、電荷Q[C]を充電してから電圧源を外した。このとき、電極間の電界E＝【（イ）】[V/m]によって静電エネルギーW=【（ウ）】[J]が蓄えられている。この状態で電極間隔を増大させると静電エネルギーも増大することから、二つの電極間には静電力【（エ）】が働くことが分かる。
ただし、真空の誘電率をε0[F/m]とする。
上記の記述中の空白個所（ア）、（イ）、（ウ）及び（エ）に当てはまる組合せとして、正しいものを次の（１）～（５）のうちから一つ選べ。
| （ア） | （イ） | （ウ） | （エ） | |
| （１） | ε0A/l | Ql/(ε0A) | Q2l/(ε0A) | 引力 |
| （２） | ε0A/l | Q/(ε0A) | Q2l/(2ε0A) | 引力 |
| （３） | A/(ε0l) | Ql/(ε0A) | Q2l/(2ε0A) | 斥力 |
| （４） | A/(ε0l) | Q/(ε0A) | Q2l/(ε0A) | 斥力 |
| （５） | ε0A/l | Q/(ε0A) | Q2l/(2ε0A) | 斥力 |
https://archivelog.net/denken3-kakomon/
https://archivelog.net/denken/