// google adsence用 電験３種過去問【2021年理論 問12】 | 電気主任技術者のいろは

電験３種過去問【2021年理論 問12】

2022年11月26日

【電子回路】電界磁界中の電子の速度《計算問題》

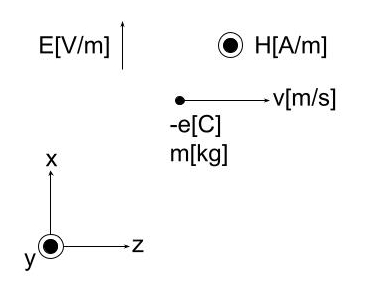
　図のように、x方向の平等電界E[V/m]、y方向の平等磁界H[A/m]が存在する真空の空間において、電荷-e[C]、質量m[kg]をもつ電子がz方向の初速度v[m/s]で放出された。この電子が等速直線運動をするとき、vを表す式として、正しいものを次の(1)～(5)のうちから一つ選べ。ただし、真空の誘電率をε0[F/m]、真空の透磁率をμ0[H/m]とし、重力の影響を無視する。
　また、電子の質量は変化しないものとする。図中の⦿は紙面に垂直かつ手前の向きを表す。

（１）\(\displaystyle \frac{ε_0 E}{μ_0 H}\)（２）\(\displaystyle \frac{E}{H}\)（３）\(\displaystyle \frac{E}{μ_0 H}\)（４）\(\displaystyle \frac{H}{ε_0 E}\)（５）\(\displaystyle \frac{μ_0 H}{E}\)

解答と解説はこちら

解答

（３）

解説

平等電界E[V/m]の影響により、電荷-e[C]の電子には、-x方向の力FE[N]が働く。

\(\displaystyle F_E=eE\text{[N]}\)

平等磁界H[A/m]の影響により、電荷-e[C]の電子には、+x方向の力FH[N]が働く。

\(\displaystyle F_H=Bev=μ_0 Hev\text{[N]}\)

題意より、この電子は、z方向の初速度v[m/s]のまま等速直線運動をするので

x方向に互いに逆向きの二つの力FE[N]とFH[N]は同じ大きさとなり、互いに打ち消し合っている。つまり、

\(\displaystyle F_E=F_H\)

\(\displaystyle ∴eE=μ_0 Hev\)

\(\displaystyle ∴v=\frac{eE}{μ_0 He}=\frac{E}{μ_0 H}\text{[m/s]}\)

<<前問　　次問>>

 

電験３種過去問理論過去問, 電験3種, 理論, 電子回路, 2021年

Posted by ちゅん