電験２種過去問【2020年理論 問2】

解答

解説

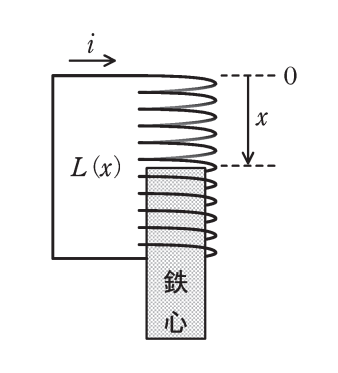
　図のようなコイルがあり、鉄心が完全に挿入された状態から x だけ引き出された時の自己インダクタンスを L(x) とする。ただし、鉄心の過電流、磁気飽和やヒステリシスは無視できるものとする。また、コイルの電気抵抗は無視でき、コイルに流れる電流は電気抵抗によって減衰しないものとする。
　鉄心の最初の位置は x=0 であり、コイルは短絡されて電流 i=I が流れ続けているものとする。このとき、コイルに鎖交する磁束数は\(\fbox{(ｲ)L(0)I}\)で、コイルが蓄えているエネルギーは\((ﾖ)\displaystyle\frac{1}{2}L(0)I^2\)である。
　次に、コイルを短絡したまま、外力を加えて鉄心を x まで引き出した。このとき、コイルに鎖交する磁束数は\(\fbox{(ｲ)L(0)I}\)のまま変わらないため、電流 i は

\(\displaystyle L(0)I=L(x)i\)

\(\displaystyle i=\frac{L(0)}{L(x)}I\)

\((ﾜ)\displaystyle\frac{L(0)}{L(x)}I\)となり、コイルが蓄えているエネルギーは

\(\displaystyle W=\frac{1}{2}L(x)i^2\)

\(\displaystyle =\frac{1}{2}L(x)\left(\frac{L(0)}{L(x)}I\right)^2\)

\((ﾛ)\displaystyle\frac{1}{2}\frac{L(0)^2}{L(x)}I^2\)に変化する。また、外力がした仕事は\(\fbox{(ﾇ)全てコイルに蓄えられた}\)。