電気回路の学習帳

2021年1月3日2024年5月1日

電気回路の学習

電気回路について、基本的な知識をできるだけわかりやすくまとめていきます。

• 電験３種過去問【2015年理論 問7】（電気回路の基本知識）

目次

1. オームの法則
2. 交流回路
3. 共振回路
4. 過渡現象
5. 三相交流回路
6. Δ-Y回路変換

電気抵抗

物質の抵抗値Ｒ[Ω]は、抵抗率ρ[Ω・ｍ]、物質の長さｌ[ｍ]とその断面積をＳ[ｍ²]とすると、

$\displaystyle R=\rho\frac{l}{S}$[Ω]

抵抗率は鉄（ρ＝8.90×10^-8Ω・ｍ）
アルミニウム（ρ＝2.50×10^-8Ω・ｍ）
銀（ρ＝1.47×10^-8Ω・ｍ）
銅（ρ＝1.55×10^-8Ω・ｍ）
※電験過去問題出題値

• 電験３種過去問【2020年理論 問5】（電線の抵抗値の計算）

オームの法則

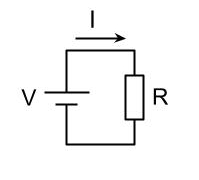
上図回路の、抵抗値R[Ω]の抵抗に、電圧V[V]が与えられたとき、流れる電流I[A]との関係は、

オームの法則　$\displaystyle V=IR$

• 電験３種過去問【2016年理論 問8】（電気の法則に関する知識）

直列回路

下図にように、抵抗が回路上に一直線に並ぶように接続される回路を、直列回路という。

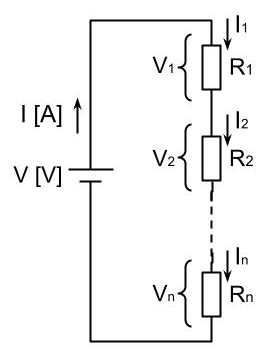
直列回路の各抵抗に流れる電流は電源に流れる電流と等しい。

直列回路の電流　$\displaystyle I=I_1=I_2=…＝I_n$

直列回路の各抵抗の電圧の合計は電源電圧と等しい。

直列回路の電圧　$\displaystyle V=V_1+V_2+…+V_n$

直列回路の合成抵抗は、各抵抗の和となる。

直列回路の合成抵抗　$\displaystyle R=R_1+R_2+…+R_n$

並列回路

下図のように抵抗が回路上で分岐して接続される回路を、並列回路という。

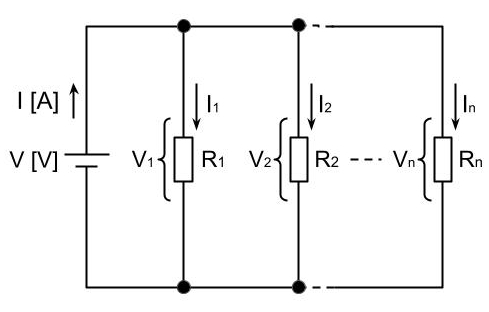
並列回路の各抵抗に流れる電流の合計は、電源に流れる電流と等しい。

並列回路の電流　$\displaystyle I=I_1+I_2+…+I_n$

並列回路の各抵抗にかかる電圧は電源電圧と等しい。

並列回路の電圧　$\displaystyle V=V_1=V_2=…=V_n$

並列回路の合成抵抗の逆数は、各抵抗の逆数和となる。

並列回路の合成抵抗　$\displaystyle \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+…+\frac{1}{R_n}$

二つの抵抗の並列回路の合成抵抗Rは、各抵抗をそれぞれ$\displaystyle R_1$及び$\displaystyle R_2$とすると、

二つの抵抗のみの並列合成抵抗　$\displaystyle R=\frac{R_1R_2}{R_1+R_2}$

• 電験３種過去問【2021年理論 問6】（直流安定化電源の動作モード）
• 電験３種過去問【2019年理論 問5】（電位差の計算）
• 電験２種過去問【2019年理論 問6】（直流回路に流れる電流の計算）

コンデンサの合成静電容量

並列に接続した二つのコンデンサＣ₁、Ｃ₂を一つのコンデンサに置き換えて考えると、合成静電容量はＣ₁、Ｃ₂の静電容量の和である。

抵抗値の温度変化

t₁[℃]における抵抗値がR₁[Ω]、抵抗温度係数がα[℃⁻¹]の抵抗器Aがある。t₂[℃]における抵抗値R₂[Ω]とするとその変化は、

R₂＝{(1+α(t₂-t₁)}R₁[Ω]

変化率は　(R₂－R₁)／R₂で表す。

• 電験３種過去問【2023年(上期)理論 問7】（抵抗の温度変化による電流値計算）
• 電験３種過去問【2011年理論 問5】（抵抗温度係数による抵抗変化）

抵抗の消費電力

可変抵抗Ｒ[Ω]で消費される電力Ｐ[Ｗ]は

$\displaystyle P=IR=I^2R=\frac{V^2}{R}$[W]

• 電験３種過去問【2021年理論 問7】（可変抵抗で消費される最大電力）
• 電験３種過去問【2020年理論 問6】（抵抗での消費電力計算）
• 電験３種過去問【2019年理論 問6】（抵抗で消費される電力計算）
• 電験３種過去問【2018年理論 問5】（抵抗器の許容電力計算）

ジュールの法則

ジュールの法則は、Q=I²Rt[J]で与えられる。（Qは生み出される熱量、Iは電流[A]、Rは電気抵抗[Ω]、ｔは電流が流れる時間[ｓ]）したがって、「電流の値の2乗と導体の抵抗に比例する」

• 電験３種過去問【2016年理論 問8】（電気の法則に関する知識）

重ね合わせの理

ある直流回路において、重ね合わせの理を用いて抵抗R_Xを流れる電流Iについて解析する。
重ね合わせの理は、線形回路において成立する定理である。ある回路において、電圧源を残して電流源を取り除いた回路を考え（このとき、電流源は開放除去されている）、抵抗R_Xに流れる電流I_aを求める。

次に、当該回路において、電流源を残して電圧源を取り除いた回路を考え（このとき電圧源は短絡除去されている）、抵抗R_Xに流れる電流I_bを求める。

電流I_aとI_bを重ね合わせれば、抵抗R_Xに流れる電流は

$\displaystyle I＝I_a+I_b\text{[A]}$

• 電験３種過去問【2023年(上期)理論 問6】(直流回路の抵抗に流れる電流計算)
• ★電験３種過去問【2023年(上期)理論 問5】（直流回路の抵抗消費電力計算）
• ★電験３種過去問【2013年理論 問6】（直流回路の抵抗消費電力計算）

• 電験２種過去問【2021年電力 問3】（重ね合わせの理による計算）
• 電験２種過去問【2019年理論 問2】（直流と交流が混在する回路の電流と電圧）

テブナンの定理

テブナンの定理は複雑な回路網中の、任意の点に流れる電流を求めるのに適している。知りたい電流が流れる点を回路から切り離し、その間の等価電源V0を求める。また電源を短絡した状態で回路側の等価抵抗R0を求める。

テブナンの定理を用いれば、等価電源V₀[V]と等価抵抗R₀[Ω]に、抵抗R[Ω]を接続したときの電流I[A]は

I=V₀/(R₀+R)[A]となる。

• 電験３種過去問【2020年理論 問7】（ブリッジ回路の計算）
• 電験２種過去問【2020年理論 問3】（テブナンの定理を用いた最大消費電力計算）

• 電験１種過去問【2013年理論 問2】（直流回路の最小電流条件計算）
• 電験１種過去問【2009年理論 問6】（直流回路網の計算）

ミルマンの定理

• 電験１種過去問【2010年理論 問2】（ミルマンの定理を用いた最大電力計算）

交流回路

• 電験３種過去問【2014年理論 問10】（RLC交流回路の知識）

正弦波交流波形

正弦波交流電圧波形の位相差をθ[rad]とすると、正弦波交流電圧の瞬時値v(t)[V]は以下となる。

$\displaystyle v(t)=V_{rms}\sqrt2\sin\left(ωt+θ\right)\text{[V]}$

$\displaystyle \omega=2\pi f$

周期T[s]と周波数f[Hz]の関係は$\displaystyle f=\frac{1}{T}$

正弦波交流波形の実効値

正弦波交流波形における、実効値V_rms[V]と波高値V_m[V]の関係は、

$\displaystyle V_m=\sqrt{2}V_{rms}\text{[V]}$

交流波形の実効値の求め方はこちら

正弦波交流波形の平均値

平均値をVa[V]とすると、平均値と最大値の関係は、

$\displaystyle V_a=\frac{2V_{m}}{\pi}\text{[V]}$

交流波形の平均値の求め方はこちら

• 電験３種過去問【2021年理論 問8】（正弦波交流電流の瞬時値）
• 電験３種過去問【2009年理論 問9】（正弦波電流の瞬時値）

リアクタンス

$\displaystyle X_L=2\pi fL=\omega L$

リアクタンスを流れる電流の位相は回路に加えた電圧より90°遅れる

• 電験３種過去問【2023年(上期)理論 問9】（RL直列回路の力率）

キャパシタンス

$\displaystyle X_C=\frac{1}{2\pi f C}=\frac{1}{\omega C}$

キャパシタンスを流れる電流の位相は回路に加えた電圧より90°進む

• 電験３種過去問【2020年理論 問8】（RC交流回路の計算）
• 電験３種過去問【2013年理論 問7】（RC直列回路の計算）
• 電験２種過去問【2021年理論 問4】（角周波数による合成リアクタンスの変化）

電力・力率

RLC直列回路の電力P[W]及び皮相電力S[V・A]を使って回路の力率cosθを表すと、cosθ＝P/Sとなる。

• 電験３種過去問【2015年理論 問8】（RL直列回路の電力計算）
• 電験３種過去問【2010年理論 問8】（RLC回路のリアクタンス・力率）
• 電験２種過去問【2020年理論 問5】（交流回路の力率とアドミタンス）

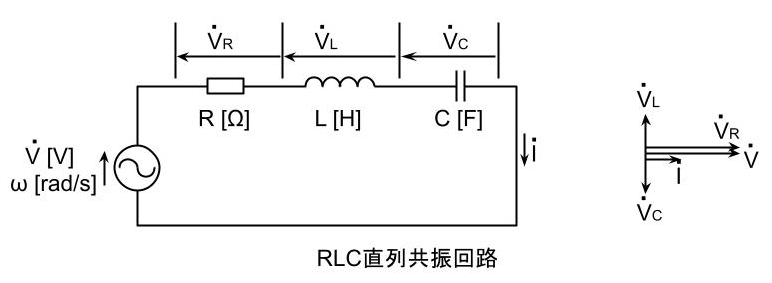
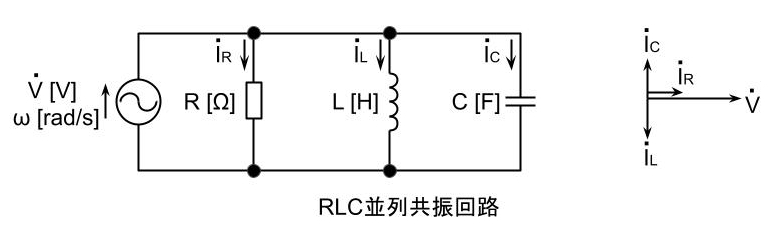
RLC共振回路

R[Ω]の抵抗、インダクタンスL[H]のコイル、静電容量C[F]のコンデンサを直列又は並列に接続した回路がある。

直列接続の場合、この回路に交流電圧を加え、その周波数を変化させると、特定の周波数ｆr[Hz]のときに誘導性リアクタンス＝２πｆrＬ[Ω]と容量性リアクタンス＝１／（２πｆrC）[Ω]の大きさが等しくなり、その作用が互いに打ち消しあって回路のインピーダンスが小さくなり、大きな電流が流れるようになる。この現象を直列共振といい、このときの周波数ｆr[Hz]をその回路の共振周波数という。

RLC直列回路及びRLC並列回路の共振条件は、LによるインピーダンスZ_L[Ω]とCによるインピーダンスZ_C[Ω]が等しいことである。つまり、

$\displaystyle Z_L=Z_C$

すなわち、

$\displaystyle ωL=\frac{1}{ωC}$

$\displaystyle ω=\frac{1}{\sqrt{LC}}$

$\displaystyle 2\pi f=\frac{1}{\sqrt{LC}}$

$\displaystyle f=\frac{1}{2\pi\sqrt{LC}}$

回路の電源周波数$\displaystyle f=\frac{1}{2\pi\sqrt{LC}}$が成り立つとき、RLC回路は共振状態となる。

回路のリアクタンスは共振周波数ｆr[Hz]より低い周波数では容量性となり、電圧より位相が進んだ電流が流れる。また、共振周波数ｆr[Hz]より高い周波数では誘導性となり、電圧より位相が遅れた電流が流れる。

RLC直列回路が共振状態の場合、回路のインピーダンスZ[Ω]は、Z＝R[Ω]となり、回路に加えた電圧と電流は同相になる。

• ★電験３種過去問【2023年(上期)理論 問8】（RLC直列共振回路）
• 電験３種過去問【2021年理論 問9】（RLC共振回路の動作）
• 電験３種過去問【2020年理論 問9】（共振回路のベクトル図）
• ★電験３種過去問【2012年理論 問7】（RLC直列共振回路）

ひずみ波交流

ひずみ波電流が以下のように直流成分$I_0とi_n$の合成で与えられるとき、

$i=I_0+i_1+i_2…+i_n$
$=I_0+\sqrt2I_1\sin(\omega t+\phi_1+\theta_1)+\sqrt2I_2\sin(2\omega t+\phi_2+\theta_2)…+\sqrt2I_n\sin(n\omega t+\phi_n+\theta_n)$

ひずみ波交流電流の実効値Iは、

$I=\sqrt{I_0^2+I_1^2+…+I_n^2}$[A]となる

• 電験３種過去問【2017年理論 問9】（ひずみ波交流の平均電力計算）

過渡現象

インダクタンスLに流れる電流と電圧

インダクタンス L [H]のコイルに、電流 i [A]が流れるとき、コイルに発生する電圧v [V]は、
$\displaystyle v=L\frac{di}{dt}$[V]

• 電験３種過去問【2023年(上期)理論 問10】（電流によりコイルに発生する電圧）
• 電験３種過去問【2022年(前期)機械 問16】（IGBTを用いた単相ブリッジ接続電圧形インバータ）

RL直列回路

開放電圧がV[V]で出力抵抗が十分に低い直流電圧源と、インダクタンスがL[H]のコイルが与えられ、抵抗R[Ω]がスイッチSを介して直列接続されている。時刻t＝0でスイッチSを閉じ、コイルの電流i_L[A]の時間に対する変化を計測して、波形として表す。

RL直列回路へ、時刻t=0[s]から、直流電源V[V]を与えるとき回路に流れる電流i(t)[A]は、

$\displaystyle i(t)=\frac{V}{R}(1-e^{-\frac{R}{L}t})\text{[A]}$

となる。

過渡電流の時間変化の指標となる時定数τは、指数(e)係数の逆数であるので

$\displaystyle τ=\frac{L}{R}\text{[s]}$

過渡電流の時定数は、最終電流$\displaystyle I=\frac{V}{R}\text{[A]}$の$\displaystyle (1-e^{-1})≒0.632$倍すなわち63.2[％]となる時間である。

• 電験３種過去問【2023年(前期)機械 問13】(RL回路の周波数伝達関数)

• 電験１種過去問【2011年理論 問4】（RL直列回路の方形バルス電圧での過渡現象）

RC直列回路

開放電圧がV[V]で出力抵抗が十分に低い直流電圧源と、キャパシタンスがC[F]のコンデンサが与えられ、抵抗R[Ω]がスイッチSを介して直列接続されている。時刻t＝0でスイッチSを閉じ、コンデンサの電流i_C[A]の時間に対する変化を計測して、波形として表す。

$\displaystyle i(t)=\frac{V}{R}e^{-\frac{1}{CR}t}$[A]となる。

• 電験３種過去問【2021年理論 問10】（RL直列回路の過渡現象）
• 電験３種過去問【2020年理論 問10】（テブナンの定理を用いたCR直列回路の時定数）
• 電験３種過去問【2018年理論 問10】（RC直列回路の時定数）
• 電験３種過去問【2022年(後期)機械 問16】（単相ブリッジ接続インバータ）

• 電験２種過去問【2021年理論 問5】（LCR直列回路の過渡現象）
• 電験２種過去問【2020年理論 問4】（RC直列回路の電圧に関する過渡現象）
• 電験２種過去問【2019年理論 問3】（直流回路のコンデンサ電圧の過渡現象）

• 電験１種過去問【2013年理論 問3】（RC回路の過渡応答）
• 電験１種過去問【2009年理論 問3】（RC直列回路過渡現象のラプラス変換による解析）

分布定数回路

• 電験１種過去問【2012年理論 問3】（分布定数回路に関する記述）
• 電験１種過去問【2010年理論 問3】（分布定数回路：線路終端に流れる電流）

3相交流回路

Y結線の対称三相交流電源にY結線の平衡三相抵抗負荷を接続した場合を考える。負荷側における線間電圧を$V_l$[V]、線電流を$I_l$[A]、相電圧を$V_p$[V]、相電流を$I_p$[A]、各相の抵抗を$R$[Ω]、三相負荷の消費電力を$P$[W]とする。

（１）$V_l=\sqrt3V_p$が成り立つ。

（２）$I_l=I_p$が成り立つ。

（３）$\displaystyle I_l=\frac{V_p}{R}$成り立つ。

（４）$P=3V_pI_p=\sqrt3V_lI_l$が成り立つ。

（５）電源と負荷の中性点を中性線で接続しても、中性線に電流は流れない。

• 電験３種過去問【2021年理論 問15】（三相平衡負荷の計算）
• 電験３種過去問【2010年理論 問9】（平衡三相交流負荷の電力）

• 電験１種過去問【2013年理論 問5】（三相交流回路に関する記述）
• 電験１種過去問【2012年理論 問5】（不平衡負荷の三相交流回路）
• 電験１種過去問【2009年理論 問2】（三相交流回路）

Δ-Ｙ変換

Δ回路に負荷抵抗$R_{Δab},R_{Δbc},R_{Δca}$[Ω]が接続されているとき、これをY回路に変換したときの平衡負荷$R_{Ya},R_{Yb},R_{Yc}$[Ω]は、

$\displaystyle R_{Ya}=\frac{R_{Δab}R_{Δca}}{R_{Δab}+R_{Δbc}+R_{Δca}}$[Ω]
$\displaystyle R_{Yb}=\frac{R_{Δab}R_{Δbc}}{R_{Δab}+R_{Δbc}+R_{Δca}}$[Ω]
$\displaystyle R_{Yc}=\frac{R_{Δbc}R_{Δca}}{R_{Δab}+R_{Δbc}+R_{Δca}}$[Ω]
となる。

$\displaystyle R_{Δab}=\frac{R_{Ya}R_{Yb}+R_{Yb}R_{Yc}+R_{Yc}R_{Ya}}{R_{Yc}}$[Ω]
$\displaystyle R_{Δbc}=\frac{R_{Ya}R_{Yb}+R_{Yb}R_{Yc}+R_{Yc}R_{Ya}}{R_{Ya}}$[Ω]
$\displaystyle R_{Δca}=\frac{R_{Ya}R_{Yb}+R_{Yb}R_{Yc}+R_{Yc}R_{Ya}}{R_{Yb}}$[Ω]
となる。

Δ回路に全て同じ平衡負荷抵抗R_Δ[Ω]が接続されているとき、これをY回路に変換したときの平衡負荷R_Y[Ω]は、

$\displaystyle R_Y=\frac{R_Δ}{3}$[Ω]となる。

• 電験３種過去問【2020年理論 問15】（単相電力計の計算）

• 電験１種過去問【2012年理論 問2】（直流回路でのΔ-Y変換計算）

非対称三相交流回路

• 電験１種過去問【2010年理論 問5】（非対称三相Y形負荷回路の電流計算）

最大値計算

最大値計算については解相加相乗平均比較法の解説を参照

• 電験３種過去問【2021年理論 問7】（可変抵抗で消費される最大電力）
• 電験２種過去問【2020年理論 問3】（テブナンの定理を用いた最大消費電力計算）
• 電験１種過去問【2010年理論 問2】（ミルマンの定理を用いた最大電力計算）