電験２種過去問【2019年理論 問2】

解答

解説

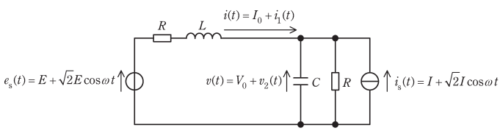
　図のように、直流と角周波数ωの正弦波交流からなる理想電圧源\(e_S(t)=E+\sqrt2E\cos\omega t\)と理想電流源\(i_S(t)=I+\sqrt2I\cos\omega t\)が接続された回路を考える。定常状態での図の電流\(I_0+i_1(t)\)と\(v(t)=V_0+v_2(t)\)を求めたい。ただし、\(I_0とV_0\)は直流成分を、\(i_1(t)とv_2(t)\)は交流成分を表し、E＞０，I＞０とする。
　回路の直流解析を行うと、重ねの理により

\(I_0=(ﾜ)\displaystyle\frac{E}{2R}-\frac{I}{2}\)

\(V_0=(ﾙ)\displaystyle\frac{E}{2}+\frac{RI}{2}\)

となる。
　次に実効値を用いて、\(e_S(t),i_S(t)\)の交流成分の複素表示及び\(i_1(t),v_2(t)\)の複素表示を、それぞれ\(\dot{E},\dot{I}及び\dot{I_1},\dot{V_2}\)とすると、回路の交流解析は、

\(\displaystyle \dot{E}=(R+j\omega L)\dot{I_1}+\dot{V_2}\)

\(\displaystyle \dot{I}=-\dot{I_1}+\frac{\dot{V_2}}{\frac{-j\frac{R}{\omega C}}{R-j\frac{1}{\omega C}}}\)

\(\displaystyle =-\dot{I_1}+\frac{R-j\frac{1}{\omega C}}{-j\frac{R}{\omega C}}\dot{V_2}\)

\(\displaystyle =-\dot{I_1}+\left(\frac{1}{R}+j\omega C\right)\dot{V_2}\)

であるので、
　\(\small{\left[\begin{array}{c}\dot{E}\\ \dot{I}\\ \end{array}\right]=\left[\begin{array}{cc}(ﾘ)R+j\omega L&1\\-1&(ﾛ)\frac{1}{R}+j\omega C\\ \end{array}\right]\left[\begin{array}{c}\dot{I_1}\\ \dot{V_2}\\ \end{array}\right]}\)　…①
となる。この表現は２端子対回路のHパラメータ表現に他ならない。ここで、\(\displaystyle \dot{E}=R\dot{I},R=\omega L,\frac{1}{R}=\omega C\)と仮定し、①式を解くと、
　\(\displaystyle\small{\left[\begin{array}{c}\dot{I_1}\\ \dot{V_2}\\ \end{array}\right]=\frac{1}{(1+j)^2+1}\left[\begin{array}{cc}(ﾛ)\frac{1}{R}+j\omega C&-1\\1&(ﾘ)R+j\omega L\\ \end{array}\right]\left[\begin{array}{c}\dot{E}\\ \dot{I}\\ \end{array}\right]=\frac{1}{1+j2}\left[\begin{array}{c}j\dot{I}\\(2+j)\dot{E}\\ \end{array}\right]}\)　…②
を得る。②式の結果を利用すると、

\(\displaystyle \dot{V_2}=\frac{1}{1+j2}(2+j)\dot{E}\)

\(\displaystyle =\frac{(2+j)(1-j2)}{(1+j2)(1-j2)}\dot{E}\)

\(\displaystyle =\frac{4-j3}{5}\dot{E}\)

となり、\(\displaystyle \frac{4-j3}{5}\)は、大きさ１のままで、\(\displaystyle \theta=\tan^{-1}\frac{3}{4}\)だけ遅れ成分を与えるので

交流電圧\(v_2(t)はv_2(t)=(ｲ)\displaystyle\sqrt2E\cos\left(\omega t-\tan^{-1}\frac{3}{4}\right)\)となる。