解答
\(\small{\begin{array}{cc}
\hline(1)&(ホ)&4.47\\
\hline(2)&(リ)&1.25\\
\hline(3)&(チ)&12\\
\hline(4)&(ハ)&3.63\\
\hline(5)&(ル)&1.19\\
\hline\end{array}}\)
解説
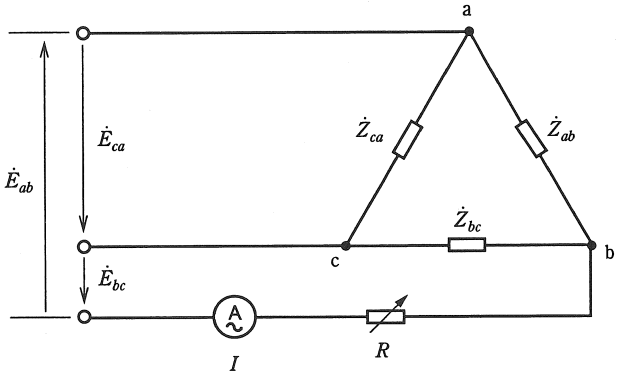
図のように、実効値が220[V]である対称三相電源\(\dot{E}_{ab}=220\angle0^{\circ}\)[V]、\(\dot{E}_{bc}=220\angle-120^{\circ}\)[V]、\(\dot{E}_{ca}=220\angle-240^{\circ}\)[V]が、Δ形三相負荷と一つの可変抵抗からなる回路に接続されている。このΔ形三相負荷の各相のインピーダンスは\(\dot{Z}_{ab}=\dot{Z}_{bc}=66+j54\)[Ω]、\(\dot{Z}_{ca}=106+j50\)[Ω]である。この回路には、実効値を指示する1個の理想的な交流電流計が図のように接続されており、その指示値をIとする。
いま、可変抵抗値をR=0[Ω]とした場合、電流計の指示値Iは、
I=\(\fbox{(ホ)4.47}\)[A]となる。
負荷の三相電力\(P_{u}\)は
\(\displaystyle |\dot{I}_{ab}|=|\dot{I}_{bc}|\)
\(\displaystyle =|\frac{\dot{E}_{ab}}{\dot{Z}_{ab}}|=\frac{220}{\sqrt{66^2+54^2}}\)
\(\displaystyle =2.579\)[A]
\(\displaystyle |\dot{I}_{ca}|=|\frac{\dot{E}_{ca}}{\dot{Z}_{ca}}|\)
\(\displaystyle =\frac{220}{\sqrt{106^2+50^2}}\)
\(\displaystyle =1.877\)[A]
\(\displaystyle P_{u}=2\times2.579^2\times66+1.877^2\times106=1251.4\)[W]
\(P_{u}=\fbox{(リ)1.25}\)[kW]となる。
次に、可変抵抗を調整したところ、各線電流の大きさは同じ値となり、回路は全体で平衡状態となった。
Δ形三相負荷を、Y形三相負荷に変換すると
\(\displaystyle |\dot{Z}_{a}|=|\dot{Z}_{c}|\)
\(\displaystyle =|\frac{\dot{Z}_{ab}\dot{Z}_{ca}}{\dot{Z}_{ab}+\dot{Z}_{bc}+\dot{Z}_{ca}}|\)
\(\displaystyle =|\frac{(66+j54)(100+j50)}{238+j158}|\)
\(\displaystyle =|\frac{4296+j9024}{238+j158}|\)
\(\displaystyle =|\frac{9024}{158}\frac{0.476+j}{1.506+j}|\)
\(\displaystyle =|\frac{9024}{158}\frac{(0.476+j)(1.506-j)}{3.268}|\)
\(\displaystyle =|17.477(1.717+j1.03)|\)
\(\displaystyle =30+j18\)[Ω]
\(\displaystyle |\dot{Z}_{b}|=|\frac{\dot{Z}_{ab}\dot{Z}_{bc}}{\dot{Z}_{ab}+\dot{Z}_{bc}+\dot{Z}_{ca}}|\)
\(\displaystyle =|\frac{(66+j54)^2}{238+j158}|\)
\(\displaystyle =|\frac{1440+j7128}{238+j158}|\)
\(\displaystyle =|\frac{7128}{158}\frac{0.202+j}{1.506+j}|\)
\(\displaystyle =|\frac{7128}{158}\frac{(0.202+j)(1.506-j)}{3.268}|\)
\(\displaystyle =|13.805(1.304+j1.304)|\)
\(\displaystyle =18+j18\)[Ω]
この場合、可変抵抗の調整値は、\(|\dot{Z}_{a}|=|\dot{Z}_{b}|=|\dot{Z}_{b}+R|\)となる条件であるので
R=\(\fbox{(チ)12}\)[Ω]となり、電流計の指示値は、
\(\displaystyle I=\frac{\frac{220}{\sqrt3}}{|\dot{Z}_{a}|}=\fbox{(ハ)3.63}\)[A]である。
また、可変抵抗とΔ形三相負荷からなる回路の総電力\(P_{b}\)は、
\(\displaystyle P_{b}=3\times3.63^2\times30=1185.9\)[W]
つまり、\(\fbox{(ル)1.19}\)[kW]である。

ディスカッション
コメント一覧
まだ、コメントがありません