電験３種過去問【2020年理論 問15】

解答

（a)の解答は（２）
（b)の解答は（３）

解説

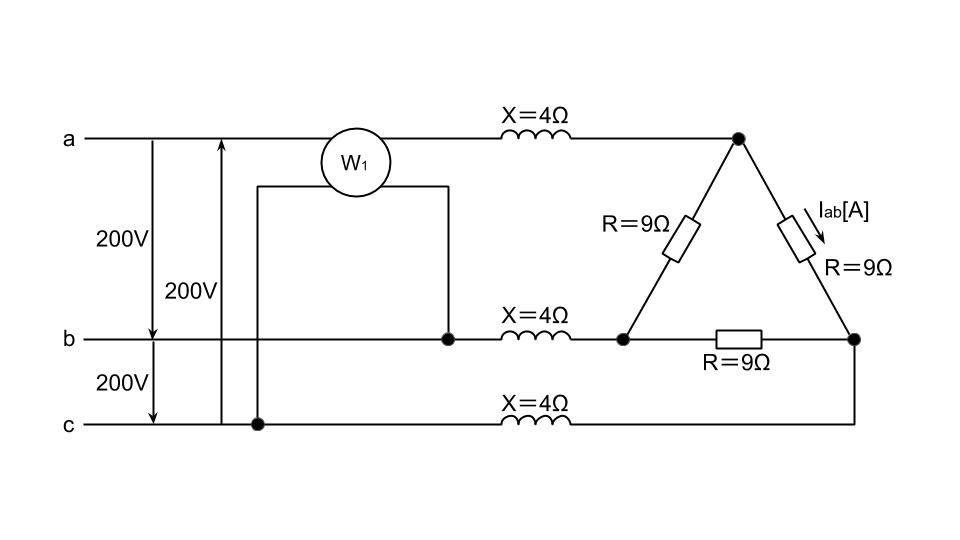
（a）電流I_ab[A]を求めるために、R=9ΩのΔ回路をY回路に変換する。

Δ回路に全て同じ平衡負荷抵抗R_Δ[Ω]が接続されているとき、これをY回路に変換したときの平衡負荷R_Y[Ω]は、

\(\displaystyle R_Y=\frac{R_Δ}{3}\)[Ω]となる。

つまり、Y回路に変換された後の平衡負荷抵抗R_Y[Ω]は

\(\displaystyle R_Y=\frac{9}{3}=3\)[Ω]

Y回路に変換後の1相分の回路は、X=4ΩとR_Y=3Ωが直列に接続され、a相を考えると相電圧V_aは\(\frac{200}{\sqrt{3}}\)[V]であるので、この時の線電流I_a[A]を求めると、

\(\displaystyle I_a=\frac{V_a}{\sqrt{X^2+R_Y^2}}=\frac{\frac{200}{\sqrt{3}}}{\sqrt{4^2+3^2}}=\frac{\frac{200}{\sqrt{3}}}{5}\\
\displaystyle =\frac{40}{\sqrt{3}}\text{[A]}\)

求める電流I_ab[A]はΔ回路の相電流であるので、

\(\displaystyle I_{ab}=\frac{I_a}{\sqrt{3}}=\frac{40}{(\sqrt{3})^2}=\frac{40}{3} \\
\displaystyle=13.3\text{[A]}\)

 

（b）単相電力計W₁には（a）で求めた線電流\(I_a=\frac{40}{\sqrt{3}}\)[A]が流れている。一方、W₁に掛かる線間電圧は\(\displaystyle V_{bc}=200\)[V]である。ベクトル図を考えると、相電圧V_aに対して相電流I_aはθ[°]遅れるものとして、V_bcはV_aに対して90°遅れる。I_aがV_aに対して90°遅れる成分はI_asinθ[A]となり、W₁の指示値は同ベクトル成分の電圧と電流の積であるので、V_bc×I_asinθとなる。すなわち、

\(\displaystyle W_1=V_{bc}\times I_a\sin\theta=200\times\frac{40}{\sqrt3}\times\frac{4}{5} \\
\displaystyle=3695\text{[W]}\)

すなわち、W₁の指示値は3.7[kW]となる。