電験2種過去問【2020年理論 問4】
【電気回路】RC直列回路の電圧に関する過渡現象《空所問題》
次の文章は、回路の過渡現象に関する記述である。文中の\(\fbox{空所欄}\)に当てはまる最も適切なものを解答群の中から選べ。
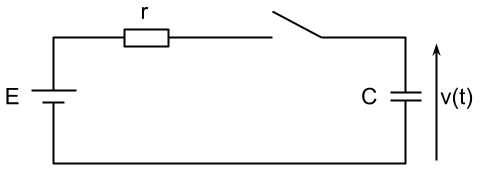
図のように、容量Cのコンデンサがスイッチを介して内部抵抗r、電圧Eの直流電源に接続されている。時刻t=0でスイッチを閉じた。
以下ではコンデンサの電圧v(t)の初期値がv(0)=0のとき、定常状態(t=∞)の電圧v(∞)は、E、C及びrの値が不明であっても、定常状態を待たずに時刻t=T、t=2T(T>0)での電圧v(T),v(2T)から求められることを示す。
t≧0におけるコンデンサの電圧v(t)の微分方程式は\(\fbox{(1)}\)で与えられる。回路の時定数τは、τ=\(\fbox{(2)}\)である。一般に、v(t)の初期値をv(0)、定常状態の値をv(∞)とすると\(\fbox{(1)}\)の解は、
\(v(t)=\)\(\fbox{(3)}\)\(+v(0)e^{-t/\tau}\) …①
で与えらえる。
コンデンサの電圧v(t)の初期値がv(0)=0のとき、v(T)とv(2T)の比は①式より
\(\displaystyle \frac{v(2T)}{v(T)}=\)\(\fbox{(4)}\) …②
となる。②式より\(e^{-T/\tau}\)を求め、これをt=Tとおいた①式に代入すると、v(0)=0より、v(T)=v(∞)×(\(\fbox{(5)}\))となる。この式より、v(∞)がv(T)とv(2T)の式で表すことが可能となる。
[問4の解答群]
\(\small{\begin{array}{ccc}
(イ)&\displaystyle E=\frac{d}{dt}v(t)+\frac{C}{r}v(t)&(ロ)&v(\infty)(1-e^{-t/\tau})&(ハ)&v(\infty)(1+e^{-t/\tau})\\
(ニ)&\displaystyle E=rC\frac{d}{dt}v(t)+v(t)&(ホ)&\displaystyle 1-\frac{v(2T)}{v(T)}&(ヘ)&\displaystyle E=C\frac{d}{dt}v(t)+\frac{1}{r}v(t)\\
(ト)&1+e^{-T/\tau}&(チ)&\displaystyle 1-2\frac{v(2T)}{v(T)}&(リ)&\displaystyle\frac{C}{r}\\
(ヌ)&rC&(ル)&e^{-T/\tau}-1&(ヲ)&1-e^{-T/\tau}\\
(ワ)&\displaystyle\frac{1}{rC}&(カ)&\displaystyle 2-\frac{v(2T)}{v(T)}&(ヨ)&v(\infty)(e^{-t/\tau}-1)\\
\end{array}}\)

 https://archivelog.net/denken/
https://archivelog.net/denken/
ディスカッション
コメント一覧
まだ、コメントがありません