電験２種過去問【2021年理論 問5】

解答

(１)：（ホ）
(２)：（ル）
(３)：（ヌ）
(４)：（ハ）
(５)：（ト）

解説

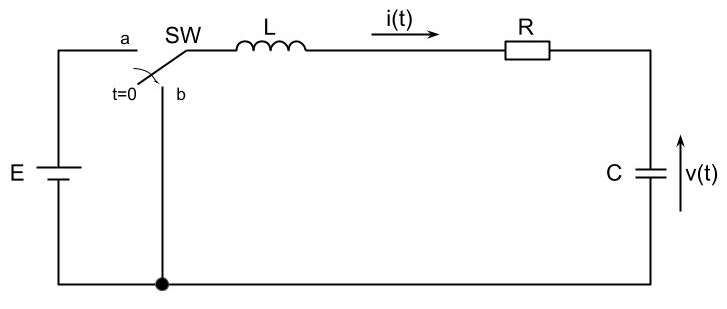
　図に示す直流電圧源Eに接続されたRLC回路のスイッチSWをa側に接続し、回路が定常状態に到達したあと、時刻t=0でスイッチSWをb側に接続した。
　t≧0での回路方程式は、コンデンサCに蓄えられた電圧v(t)が、スイッチSWのb側閉回路へ電流i(t)を供給するので、

\(\displaystyle v(t)=-Ri(t)-L\frac{di(t)}{dt}\)

\(\displaystyle L\frac{di(t)}{dt}+Ri(t)+v(t)=0\)　…　①

となる。

ここで、スイッチSWがa側に接続された定常状態では、コンデンサCには直流電源電圧Eが印加された状態であり、電流i(t)=0である。（※コンデンサ電極を開放端子とみなすことができる）

したがって、①式において、t=0のとき、\(\displaystyle v(t)=\)\(\fbox{E}\) ,\(\displaystyle i(t)=\)\(\fbox{0}\)である。

ここで、t=0のときの\(\displaystyle v(t)=\)\(\fbox{E}\) ,\(\displaystyle i(t)=\)\(\fbox{0}\)を①式に代入すると、

\(\displaystyle L\frac{di(t)}{dt}+Ri(t)+v(t)=0\)

\(\displaystyle L\frac{di(t)}{dt}+0+E=0\)

\(\displaystyle \frac{di(t)}{dt}=-\frac{E}{L}\)

つまり、\(\displaystyle \frac{di(t)}{dt}=\)\(\displaystyle -\frac{E}{L}\)であることが分かる。

①式の両辺に\(\displaystyle i(t)\)を掛けてt=0からt=∞まで積分すると、

\(\displaystyle \int_0^{∞}Ri(t)^2dt=-\int_0^{∞}L\frac{di(t)}{dt}i(t)dt-\int_0^{∞}v(t)i(t)dt\)　…　②

となる。②式に図の回路の\(\displaystyle v(t)\)と\(\displaystyle i(t)\)の関係式\(\displaystyle i(t)=C\frac{dv(t)}{dt}\)を代入すると、積分の結果は次のようになる。

\(\displaystyle \int_0^{∞}Ri(t)^2dt=-\int_0^{∞}Li(t)\frac{di(t)}{dt}dt-\int_0^{∞}Cv(t)\frac{dv(t)}{dt}dt\)

\(\displaystyle =-\int_0^{∞}Li(t)di(t)-\int_0^{∞}Cv(t)dv(t)\)

\(\displaystyle =-\frac{1}{2}L\left[i(∞)^2-i(0)^2\right]-\frac{1}{2}C\left[v(∞)^2-v(0)^2\right]\)

ここで、\(\displaystyle i(0)=0\)、また十分に時間経過すると、コンデンサCの放電は完了し\(\displaystyle i(∞)=0\)となる。さらに\(\displaystyle v(0)=E\)、また十分に時間経過すると、コンデンサCの放電は完了し\(\displaystyle v(∞)=0\)となる。

したがって、\(\displaystyle \int_0^{∞}Ri(t)^2dt=\)\(\displaystyle \frac{1}{2}CE^2\)を得る。