解答
解説
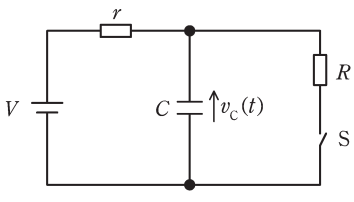
図の回路は、時刻t<0においてスイッチSは開いており、回路は定常状態にある。この回路のスイッチSを時刻t=0で閉じるものとする。
スイッチSを閉じた後、十分に時間が経過して回路が定常状態になったときのキャパシタCに電流は流れないので、その電圧は抵抗Rにかかる電圧と等しくなり、\(\displaystyle(ニ)\frac{R}{R+r}V\)である。
スイッチSを閉じた後の回路方程式は、rに流れる電流を\(i_r\)、Cに蓄えられる電荷をq、Rに流れる電流を\(i_R\)とすると、
Cに流れる電流\(\displaystyle i_C=\frac{dq}{dt}\)、Cの電圧\(\displaystyle v_C=\frac{q}{C}\)なので、
\(\displaystyle i_r=\frac{dq}{dt}+i_R\) …①
\(\displaystyle V=i_rr+\frac{q}{C}\) …②
\(\displaystyle \frac{q}{C}=i_RR\) …③
①、②より
\(\displaystyle V=r(\frac{dq}{dt}+i_R)+\frac{q}{C}\) …④
③、④より
\(\displaystyle V=r(\frac{dq}{dt}+\frac{q}{CR})+\frac{q}{C}\)
\(\displaystyle V=r\frac{dq}{dt}+\frac{r}{CR}q+\frac{1}{C}q\)
\(\displaystyle V=r\frac{dq}{dt}+\frac{R+r}{CR}q\)
一階線形微分方程式\(\displaystyle \frac{dy}{dx}+py=k\)の一般解は\(\displaystyle y=Ae^{-px}+\frac{k}{p}\)で与えられるので(Aは任意定数)、上式を展開し一般解を求めると
\(\displaystyle \frac{dq}{dt}+\frac{R+r}{CRr}q=\frac{V}{r}\)
∴\(\displaystyle q=Ae^{-\frac{R+r}{CRr}t}+\frac{\frac{V}{r}}{\frac{R+r}{CRr}}\)
\(\displaystyle =Ae^{-\frac{R+r}{CRr}t}+\frac{CR}{R+r}V\)
キャパシタCの電圧は
\(\displaystyle v_C(t)=\frac{q}{C}\)
\(\displaystyle =\frac{A}{C}e^{-\frac{R+r}{CRr}t}+\frac{R}{R+r}V\)
t=0のとき、キャパシタCには全電源電圧がかかるので、\(\displaystyle v_C(0)=V\)である。任意定数Aを求めると、
\(\displaystyle v_C(0)=\frac{A}{C}e^{-\frac{R+r}{CRr}\times0}+\frac{R}{R+r}V\)
\(\displaystyle =\frac{A}{C}+\frac{R}{R+r}V=V\)
∴\(\displaystyle \frac{A}{C}=\frac{r}{R+r}V\)
∴\(\displaystyle \frac{A}{C}=\frac{r}{R+r}V\)
∴\(\displaystyle A=\frac{Cr}{R+r}V\)
したがって、時刻t=0でスイッチSを閉じた後の過渡状態においては、回路の時定数を\(T_1\)とすれば、キャパシタCの電圧は、
\(\displaystyle v_C(t)=(ニ)\frac{R}{R+r}V+(ロ)\frac{r}{R+r}Ve^{-t/T_1},(t≧0)\)
となる。ここで回路の時定数は定義より、\(T_1=(ト)\displaystyle\frac{CRr}{R+r}\)である。
スイッチSを閉じた後、十分に時間が経過して回路が定常状態になった時刻\(t=t_0\)で、再びスイッチSを開いた。スイッチSを再び開いた後の過渡状態においては、回路に流れる電流を\(i\)、Cに蓄えられる電荷をqとすると、
\(\displaystyle ri+\frac{q}{C}=r\frac{dq}{dt}+\frac{q}{C}=V\)
∴\(\displaystyle \frac{dq}{dt}+\frac{1}{Cr}q=\frac{V}{r}\)
一般解を求めると、
\(\displaystyle q=Ae^{-\frac{t}{Cr}}+\frac{\frac{V}{r}}{\frac{1}{Cr}}\)
\(\displaystyle =Ae^{-\frac{t}{Cr}}+CV\)
上式の初期条件はt=0で\(\displaystyle v_C(t)=\frac{q}{C}=\frac{R}{R+r}V\)であるので、
\(\displaystyle \frac{A}{C}e^{-\frac{0}{Cr}}+V=\frac{R}{R+r}V\)
∴\(\displaystyle \frac{A}{C}+V=\frac{R}{R+r}V\)
∴\(\displaystyle \frac{A}{C}=-\frac{r}{R+r}V\)
したがって
\(\displaystyle v_C(t)=\frac{q}{C}=-\frac{r}{R+r}Ve^{-\frac{t}{Cr}}+V\)
\(\displaystyle =\frac{R+r}{R+r}V-\frac{r}{R+r}Ve^{-\frac{t}{Cr}}\)
\(\displaystyle =\frac{R}{R+r}V+\frac{r}{R+r}V-\frac{r}{R+r}Ve^{-\frac{t}{Cr}}\)
\(\displaystyle =\frac{R}{R+r}V+\frac{r}{R+r}V(1-e^{-\frac{t}{Cr}})\)
回路の時定数を\(T_2\)とすれば、キャパシタCの電圧は、
\(\displaystyle v_C(t)=(ニ)\frac{R}{R+r}V+(ロ)\frac{r}{R+r}((ハ)1-e^{-(t-t_0)/T_2}) ,(t≧t_0)\)
となる。ここで回路の時定数は、\(T_2=(カ)Cr\)である。

ディスカッション
コメント一覧
まだ、コメントがありません