電験３種過去問【2019年理論 問5】

解答

（５）

解説

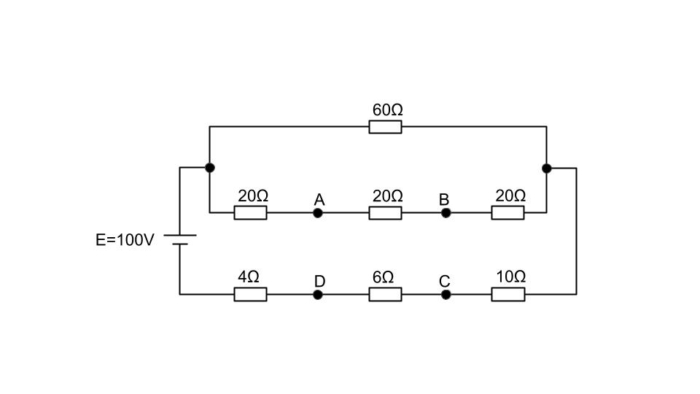
　回路の並列部分は、60Ωの抵抗と、20+20+20＝60Ωの抵抗からなる。同値の抵抗が並列に接続されているとき、並列部分の合成抵抗はそれぞれの半分となる。すなわち、30Ωである。

　回路の合成抵抗値Ｒ[Ω]は、

　R＝30+10+6+4＝50[Ω]

　この回路に流れる電流I[A]は

　I＝E/R＝100/50＝2[A]

　直流電源の負極側からみて、D点の電位V_D[V]は、

　V_D＝2×4=8[V]

　直流電源の負極側からみて、C点の電位V_C[V]は、

　V_C＝2×(4+6)=20[V]

　直流電源の負極側からみて、C点の電位V_C[V]は、

　V_C＝2×(4+6)=20[V]

　ここで、回路の並列部分のA-B点側を流れる電流は、並列回路の抵抗値が同値であるので均等に分流する。すなわちA-B点を流れる電流は1[A]である。

　したがって、直流電源の負極側からみて、Ｂ点の電位V_Ｂ[V]は、

　V_B＝2×(4+6+10)+1×20=60[V]

　直流電源の負極側からみて、A点の電位V_A[V]は、

　V_A＝2×(4+6+10)+1×(20+20)=80[V]

　題意より、A-D間の電位差V_AD[V]は

　V_AD＝V_A－V_D＝80-8＝72[V]

　また、B-C間の電位差V_BC[V]は

　V_BC＝V_B－V_C＝60-20＝40[V]