電験３種過去問【2020年理論 問10】

解答

（２）

解説

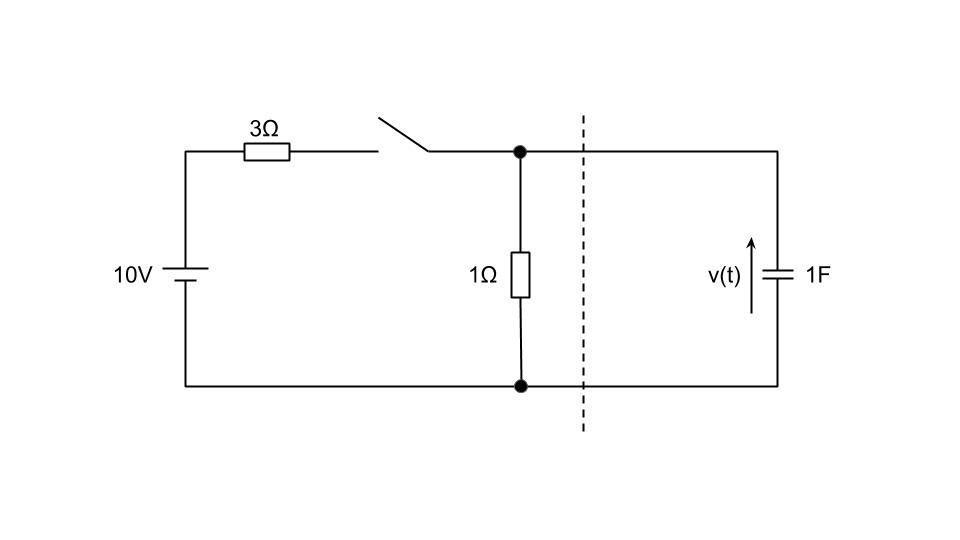
　テブナンの定理を用いて解く。テブナンの定理は複雑な回路網中の、任意の点に流れる電流を求めるのに適している。知りたい電流が流れる点を回路から切り離し、その間の等価電源V₀を求める。また電源を短絡した状態で回路側の等価抵抗R₀を求める。

　まず、題意より、1Fのコンデンサを破線部分で回路網から切り離した状態での等価電源V₀[V]は

　V₀＝10[V]×1[Ω]/4[Ω]＝2.5[V]である。

次に、等価抵抗R₀[Ω]は、電源10Vを短絡すると、3Ωと1Ωの並列抵抗であるので、和分の積を使って合成抵抗を求めると

\(\displaystyle R_0=\frac{3\times 1}{3+1}＝0.75\)[Ω] となる。

テブナンの定理を用いれば、等価電源V₀[V]と等価抵抗R₀[Ω]に、コンデンサC＝1[F]を接続したとき、CR直列回路となる。この時の電流i(t)[A]は

\(i(t)=\frac{V_0}{R_0}e^{-\frac{1}{CR_0}t}\)[A]となる。

時定数\(τ＝CR_0\)[s]であるので、\(τ＝\)1×0.75＝0.75[s]

またi(t)[A]の最終値を知るためi(∞)を求めると、

\(i(∞)=\frac{V_0}{R_0}e^{-\frac{1}{CR_0}∞}=0\)

つまり最終値i(∞)＝0[A]となり、コンデンサには電流が流れない。つまり最初に、コンデンサを切り離して求めた等価電源と同じ電圧がかかる。

　v(∞)＝V₀＝2.5[V]

したがって、v(t)の最終値は2.5[V]となる。