解答
(4)
解説
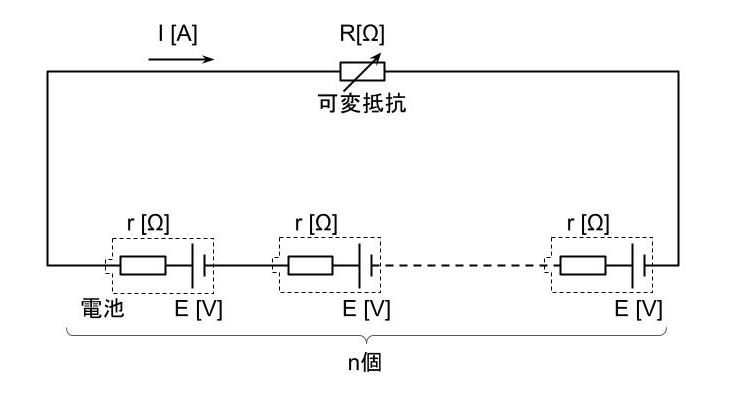
回路に流れる電流I[A]は
\(\displaystyle I=\frac{nE}{R+nr}\text{[A]}\)
可変抵抗R[Ω]で消費される電力P[W]は
\(\displaystyle P=I^2R=\left(\frac{nE}{R+nr}\right)^2R\)
\(\displaystyle =\frac{R(nE)^2}{(R+nr)^2}\)
\(\displaystyle =\frac{R(nE)^2}{R^2+2Rnr+(nr)^2}\)
\(\displaystyle =\frac{(nE)^2}{R+2nr+\frac{(nr)^2}{R}}\)
上式の分母が最小になるとき、P[W]は最大となる。
つまり、分母をRの変数となる関数f(R)とおくと、
関数f(R)が最小になるとき、P[W]は最大となる。
\(\displaystyle f(R)=R+2nr+\frac{(nr)^2}{R}\)
\(\displaystyle R=(\sqrt{R})^2\)として変形すると、
\(\displaystyle f(R)=(\sqrt{R})^2+2nr+\left(\frac{nr}{\sqrt{R}}\right)^2\)
\(\displaystyle (a-b)^2\)の形となる数式に変形すると、
\(\displaystyle f(R)=\left(\sqrt{R}-\frac{nr}{\sqrt{R}}\right)^2+4nr\)
\(\displaystyle \left(\sqrt{R}-\frac{nr}{\sqrt{R}}\right)^2=0\)となるとき、関数f(R)が最小になるので
\(\displaystyle \sqrt{R}-\frac{nr}{\sqrt{R}}=0\)で、関数f(R)は最小となる。つまり
\(\displaystyle \sqrt{R}=\frac{nr}{\sqrt{R}}\)
\(\displaystyle R=nr\)
★相加平均・相乗平均比較法はこちら
★相加相乗平均比較法で\(\displaystyle f(R)=R+2nr+\frac{(nr)^2}{R}\)が最小となる条件を求める
a>0,b>0では相加平均\(\displaystyle \frac{a+b}{2}\)は、相乗平均\(\displaystyle \sqrt{ab}\)より常に大きく、
\(\displaystyle \frac{a+b}{2}≧\sqrt{ab}\)
\(\displaystyle a+b≧2\sqrt{ab}\)
等号はa=bのときに成り立つ。
つまり、変数f(X)=a+bは\(\displaystyle a=X,b=\frac{1}{X}\)の形をとれば
a=bのときに、つまり、\(\displaystyle X=\frac{1}{X}\)のときにf(X)は最小値となる。
ここで、\(\displaystyle R+\frac{(nr)^2}{R}\)が最小であれば、f(R)は最小であるので、
\(\displaystyle R=\frac{(nr)^2}{R}\)のときに、f(R)は最小となる。つまり
\(\displaystyle R^2=(nr)^2\)
\(\displaystyle R=nr\)
★微分法はこちら
★微分法で\(\displaystyle f(R)=R+2nr+\frac{(nr)^2}{R}\)が最小となる条件を求める
関数f(R)は\(\displaystyle R\)と\(\displaystyle \frac{1}{R}\)の合成であるので、
R>0では、Rが大きくなるにつれて、
f(R)は∞から最小値へ向かい、最小値からRに比例する関数に近づくように増加する。
関数f(R)を微分すると
\(\displaystyle f'(R)=1-\frac{(nr)^2}{R^2}\)
関数f’(R)=0は、f(R)の傾きが0となる点、すなわち最小値を示すので
\(\displaystyle f'(R)=1-\frac{(nr)^2}{R^2}=0\)
\(\displaystyle \frac{(nr)^2}{R^2}=1\)
\(\displaystyle R^2=(nr)^2\)
\(\displaystyle R=nr\)
つまり、R=nr[Ω]のとき、消費電力P[W]は最大となる。このときの電流I[A]は
\(\displaystyle I=\frac{nE}{R+nr}\text{[A]}\)
上式に、R=nr[Ω]を代入して
\(\displaystyle I=\frac{nE}{nr+nr}=\frac{nE}{2nr}=\frac{E}{2r}\text{[A]}\)

 https://archivelog.net/denken/
https://archivelog.net/denken/
ディスカッション
コメント一覧
まだ、コメントがありません