電験３種過去問【2021年理論 問10】

解答

（４）

解説

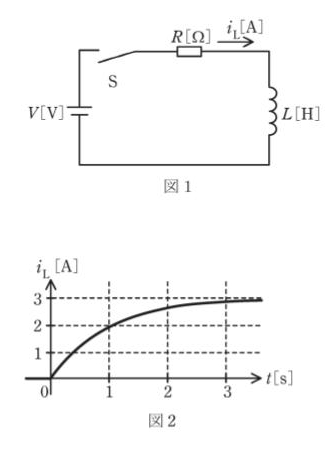
RL直列回路へ、時刻t=0[s]から、直流電源V[V]を与えるとき回路に流れる電流i(t)[A]は、

$\displaystyle i(t)=\frac{V}{R}(1-e^{-\frac{R}{L}t})\text{[A]}$

となる。

過渡電流の時間変化の指標となる時定数τは、指数(e)係数の逆数であるので

$\displaystyle τ=\frac{L}{R}\text{[s]}$

題意では、過渡電流の時定数は、最終電流$\displaystyle I=\frac{V}{R}\text{[A]}$の$\displaystyle (1-e^{-1})≒0.632$倍すなわち63.2[％]となる時間である。

 

抵抗値R=1Ωでの最終電流I₁[A]は

$\displaystyle I_1=\frac{V}{R}=V\text{[A]}$

抵抗値R=2Ωでの最終電流I₂[A]は

$\displaystyle I_2=\frac{V}{R}=\frac{V}{2}\text{[A]}$

つまり抵抗値R=2Ωでの最終電流I₂は、I₁の$\displaystyle\frac{1}{2}$となる。

 

抵抗値R=1Ωでの時定数τ₁[s]は

$\displaystyle τ_1=\frac{L}{R}=L\text{[s]}$

抵抗値R=2Ωでの時定数τ₂[s]は

$\displaystyle τ_2=\frac{L}{R}=\frac{L}{2}\text{[s]}$

つまり抵抗値R=2Ωでの時定数τ₂は、τ₁の$\displaystyle\frac{1}{2}$となる。

 

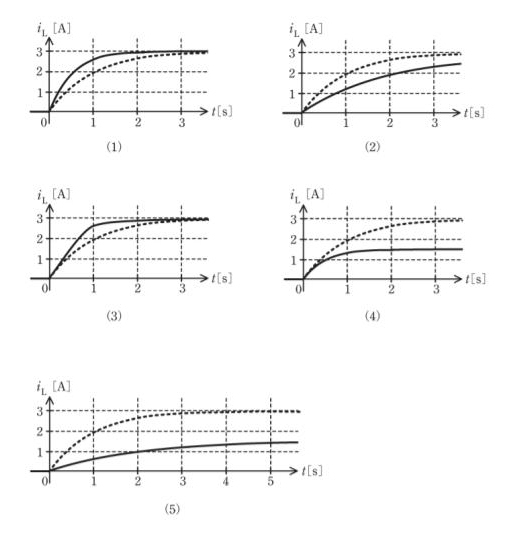
したがって、R=2Ωとしたとき、R=1Ωのときと比べて、

最終電流i_L[A]は$\displaystyle\frac{1}{2}$となり、

最終電流の63.2[％]となる時間である、時定数は$\displaystyle\frac{1}{2}$となる。つまり過渡電流の時間変化は2倍速い。

以上より(4)が正解となる。