電験３種過去問【2021年理論 問15】

解答

（a）：（２）
（b）：（１）

解説

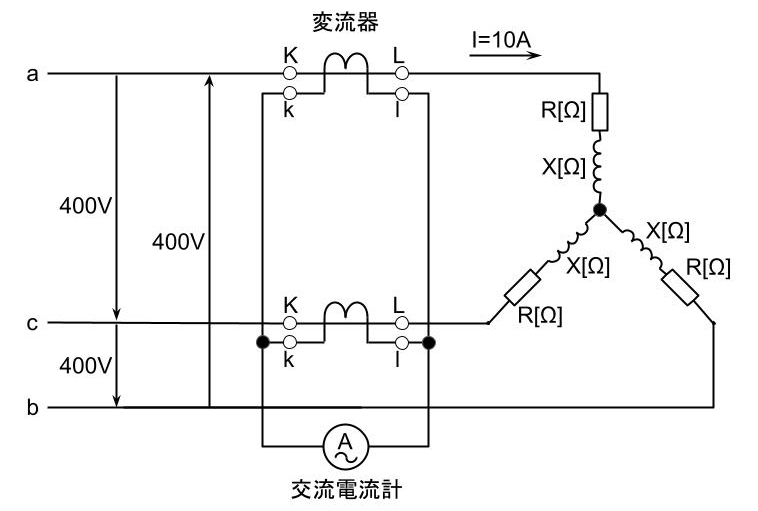
（a）題意より、対称三相交流電源に平衡三相負荷が接続されているので、線電流Ia=Ib=Ic＝10Aとなる。

a相及びc相の変流器の2次側に、Ia’及びIc’の電流が流れるとすると、

変流器の変流比が20：5であるので、

\(\displaystyle I_a’=I_c’=I\times \frac{5}{20}\)

\(\displaystyle =10 \times \frac{5}{20}=2.5\text{[A]}\)

変流器は電流Ia及びIcの方向に対して、同極性で接続されているため、

交流電流計には、下図のような電流Ia’及びIc’のベクトル合成電流が表れる。

 

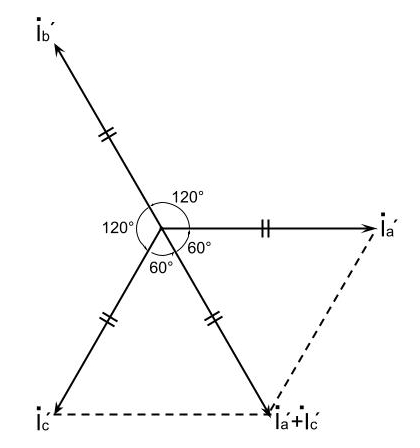
ベクトル図より、

\(\displaystyle \left|\vec{I_a’}+\vec{I_c’}\right|=\left|\vec{I_a’}\right|=\left|\vec{I_c’}\right|\)

したがって、電流計に現れる電流値は、2.5[A]となる。

（b）平衡三相負荷の全消費電力P[W]は、線間電圧V[V]、線電流I[A]、負荷力率cosθとすると、

\(\displaystyle P=\sqrt3 VIcos\theta\text{[W]}\)

となる。

題意より、全消費電力P=6[kW]であるので、

\(\displaystyle 6\times10^3=\sqrt3 \times400 \times10 \times cos\theta\)

\(\displaystyle ∴cos\theta=\frac{6\times10^3}{\sqrt3 \times400 \times10}\)

\(\displaystyle =\frac{3}{2\sqrt3}\)

\(\displaystyle =\frac{\sqrt3}{2}\)

このとき、力率の遅れ角θは

\(\displaystyle \theta=30\text{[°]}\)

相電圧Vaは

\(\displaystyle V_a=\frac{V}{\sqrt3}\)

\(\displaystyle =\frac{400}{\sqrt3}\text{[V]}\)

各相の合成インピーダンスZは

\(\displaystyle Z=\frac{V_a}{I}\)

\(\displaystyle =\frac{\frac{400}{\sqrt3}}{10}=\frac{40}{\sqrt3}\text{[Ω]}\)

Z[Ω]は誘導性インピーダンスであるので、遅れ力率角θとR[Ω]、X[Ω]の関係は下図のようになる。

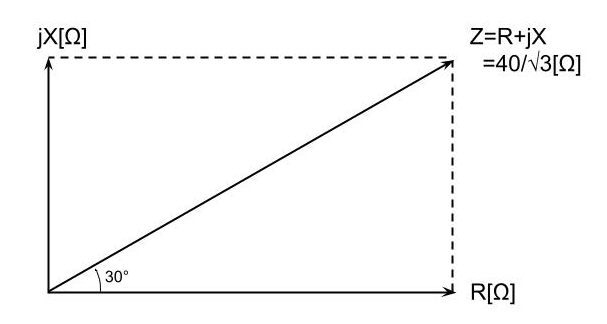
上図より、各相の抵抗R[Ω]は、力率\(\displaystyle cos30°=\frac{\sqrt3}{2}\)であるので、

\(\displaystyle R=Zcos\theta=\frac{40}{\sqrt3}\times\frac{\sqrt3}{2}\)

\(\displaystyle =20\text{[Ω]}\)

合成インピーダンスは\(\displaystyle Z=\sqrt{R^2 +X^2}\text{[Ω]}\)であるので、

\(\displaystyle X^2={Z_{RX}}^2 -R^2\)

\(\displaystyle =\left(\frac{40}{\sqrt3}\right)^2 -20^2\)

\(\displaystyle =\frac{1600-1200}{3}=\frac{400}{3}\)

したがって、

\(\displaystyle X=\sqrt{\frac{400}{3}}\)

\(\displaystyle =11.5\text{[Ω]}\)