自動制御の学習帳

2021年3月2日2024年11月2日

目次

1. 古典制御
   • 伝達関数
   • ラプラス変換
   • PID補償器
2. 現代制御

フィードバック制御の基本３動作

　目標値と制御量の差である偏差に比例して操作量を変化させる制御動作を比例動作という。この動作の場合、制御動作が働いて目標値と制御量の偏差が小さくなると操作量も小さくなるため、制御量を目標値に完全に一致させることができず、定常偏差が生じる欠点がある。
　一方、偏差の微分値に応じて操作量を変化させる制御動作を微分動作という。この動作は偏差の起こり始めに大きな操作量を与える動作をするので、偏差を早く減衰させる効果があるが、制御のタイミング（位相）によっては偏差を増幅し不安定になることがある。
　また、偏差の積分値に応じて操作量を変化させる制御動作を積分動作という。この動作は偏差が零になるまで制御動作が行われるで、定常偏差を無くすことができる。

　基本3動作を合わせた補償器をPID補償器という。

古典制御

伝達関数

出力信号y(t)のラプラス変換Y(s)と、入力信号x(t)のラプラス変換X(s)の比を伝達関数という。

$\displaystyle G(s)=\frac{Y(s)}{X(s)}$

ブロック線図

伝達関数$\displaystyle G(s)=\frac{Y(s)}{X(s)}$をブロック線図を用いて、下図のように表す。

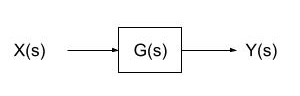
ブロック線図の等価変換

直列接続

等価伝達関数　G(s)=G₁(s)G₂(s)

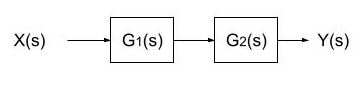
並列接続

等価伝達関数　G(s)=G₁(s)±G₂(s)

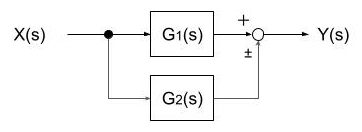
フィードバック結合

等価伝達関数$\displaystyle G(s)=\frac{G_1(s)}{1∓G_1(s)G_2(s)}$

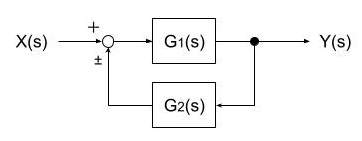
ラプラス変換表

伝達関数の基本要素

比例要素

y(t)=Kx(t)をラプラス変換すると
Y(s)=KX(s)

$\displaystyle G(s)=\frac{Y(s)}{X(s)}=K$

積分要素

$\displaystyle y(t)=K\int x(t)dt$をラプラス変換すると
$\displaystyle Y(s)=K\frac{X(s)}{s}$
$\displaystyle G(s)=\frac{Y(s)}{X(s)}=\frac{K}{s}$

微分要素

$\displaystyle y(t)=K\frac{dx(t)}{dt}$をラプラス変換すると
Y(s)=K(sX(s)-x(0))
ここで、x(0)=0とすれば
Y(s)=KsX(s)

$\displaystyle G(s)=\frac{Y(s)}{X(s)}=Ks$

一次遅れ要素

RC回路において

$\displaystyle Ri(t)+\frac{1}{C}\int i(t)dt=e_1(t)$

$\displaystyle \frac{1}{C}\int i(t)dt=e_2(t)$

上記をラプラス変換すると

$\displaystyle RI(s)+\frac{I(s)}{Cs}=E_1(s)$

$\displaystyle \frac{I(s)}{Cs}=E_2(s)$

$\displaystyle G(s)=\frac{E_2(s)}{E_1(s)}$

$\displaystyle =\frac{\frac{1}{Cs}I(s)}{\left(R+\frac{1}{Cs}\right)I(s)}$

$\displaystyle =\frac{\frac{1}{Cs}}{\left(R+\frac{1}{Cs}\right)}$

$\displaystyle =\frac{1}{1+CRs}$

$\displaystyle T=CR$を時定数とすると、

$\displaystyle G(s)=\frac{1}{1+Ts}$

周波数伝達関数

周波数伝達関数

入力信号が正弦波交流である場合、定常状態での出力信号$\displaystyle \dot{E}_o(jω)$と入力信号$\displaystyle \dot{E}_i(jω)$の比は、入力信号の角周波数ωの関数となる。これを周波数伝達関数G(jω)と呼ぶ。

$\displaystyle G(jω)=\frac{\dot{E}_o(jω)}{\dot{E}_i(jω)}$

伝達関数G(jω)は、複素数であるので、絶対値をゲインという。

$\displaystyle |G(jω)|=\frac{|\dot{E}_o(jω)|}{|\dot{E}_i(jω)|}$

伝達関数の偏角を位相角θという。

$\displaystyle \theta =\angle G(jω)$

ベクトル軌跡

ベクトル軌跡とは角周波数ωの変化に対する周波数伝達関数 G(jω) の変化を複素平面上のベクトルとして表したもの。

一巡伝達関数（開ループ伝達関数）

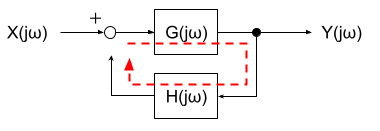
ブロック線図のループの一部を切り開いたときに、一巡する伝達関数を一巡伝達関数という。
下図の場合、一巡伝達関数は G(jω)H(jω) となる。

ナイキスト線図

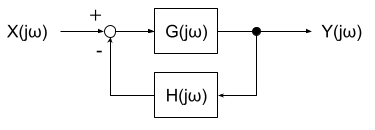
特に、下図のようなフィードバック制御系の、一巡伝達関数 G(jω)H(jω) のベクトル軌跡をナイキスト線図という。ナイキスト線図により、フィードバック制御系の安定判別ができる。

ナイキスト判別法

　ベクトル軌跡上での実軸との交点となる点（位相差が-180°となる点）での周波数を、位相交差周波数 ω₀ という。位相交差周波数 ω₀ における点が、実軸との交点で負の値をとりながら、この点が（-1，0）より右にあれば安定、左は不安定となる。（-1，0）つまり-1+ｊ0の点が安定限界となる。

ゲイン特性

伝達関数G(jω)について、横軸に角周波数ωを対数目盛でとり、縦軸にゲイン

$\displaystyle 20\log_{10}|G(jω)|$[dB]

をとったものを、ゲイン特性という。

位相特性

伝達関数G(jω)について、横軸に角周波数ωを対数目盛でとり、縦軸に位相角をとったものを、位相特性という。

ボード線図

ゲイン特性と位相特性を１組にしたものをボード線図という。

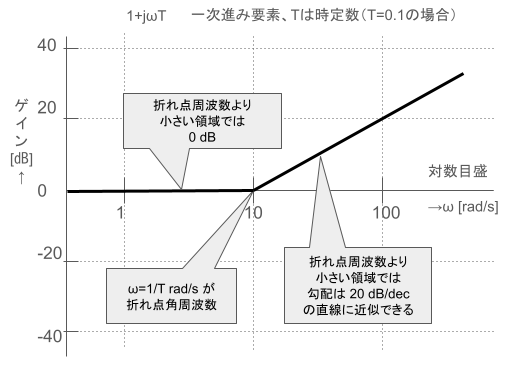
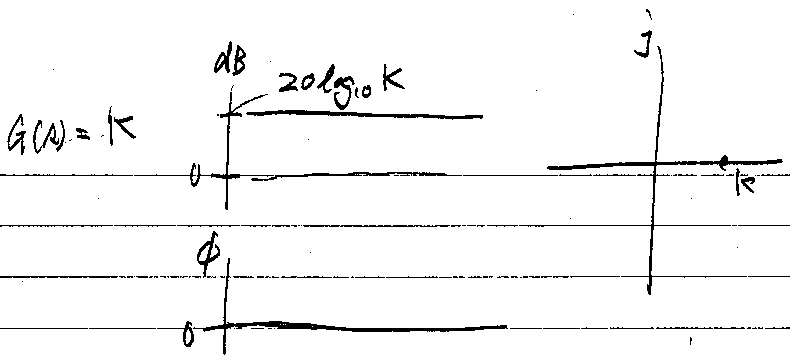
比例要素

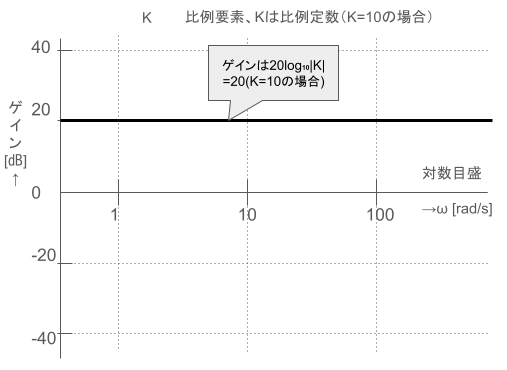
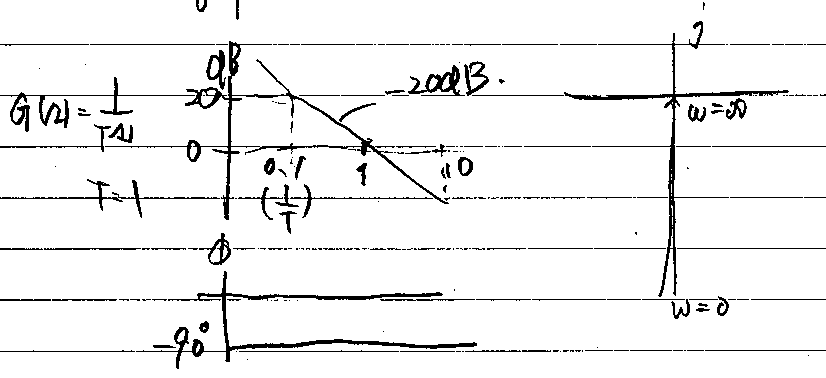
積分要素

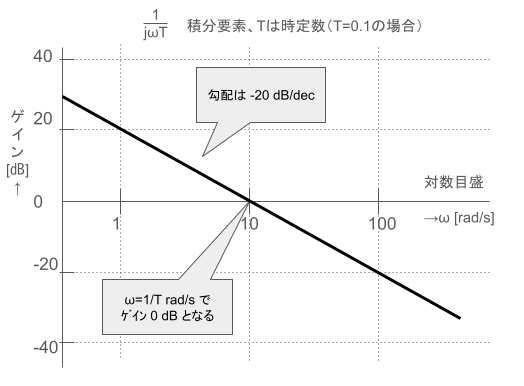
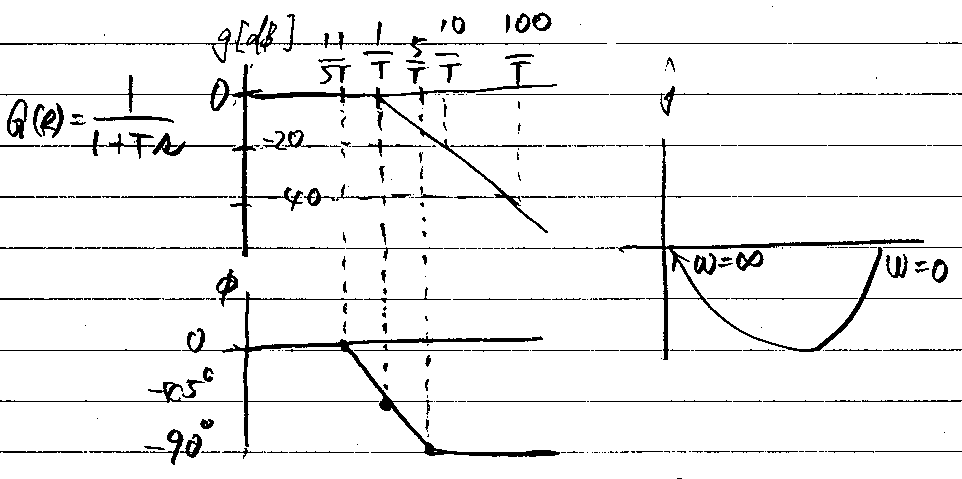
１次遅れ要素の折れ点角周波数

$\displaystyle G(s)=\frac{1}{1+τs}$

折れ点角周波数ω_c[rad/s]は、時定数τの逆数となる。

$\displaystyle ω_c=\frac{1}{τ}$

このときの周波数はカットオフ周波数と呼ばれ、

ゲイン-3dB、位相角-45°となる。

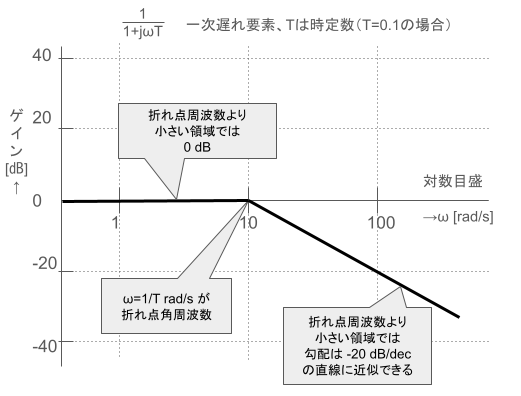
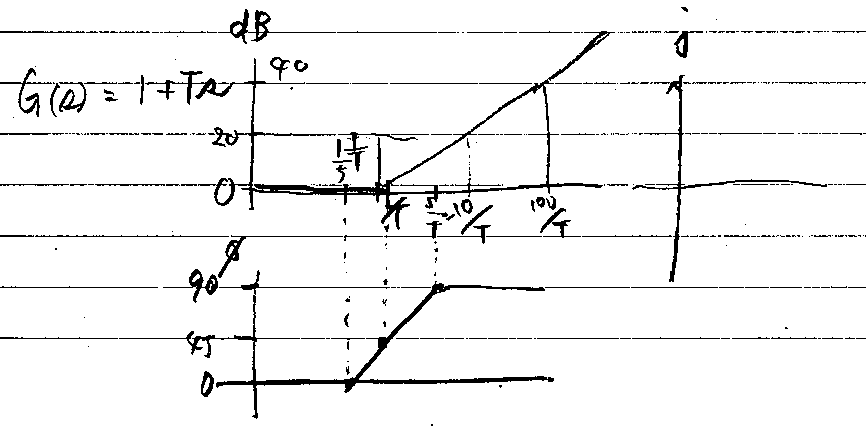
一次進み要素

ボード線図・ベクトル軌跡メモ

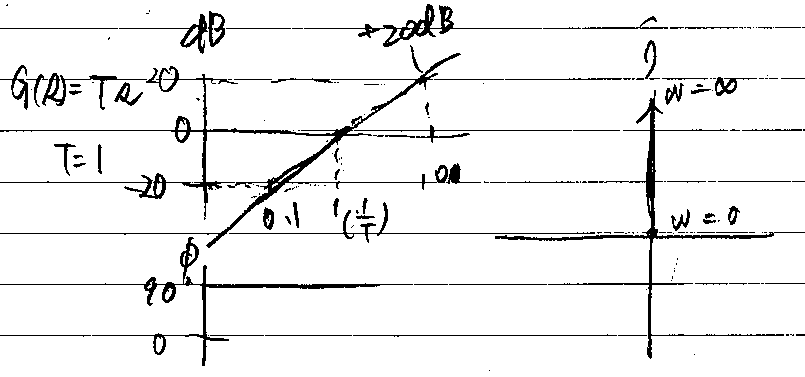
補償器

PID補償器

　PID調節計、PIDコントローラなどともいう。
$\displaystyle K(s)=K_P\left(1+\frac{1}{T_Is}+T_Ds\right)$
各係数について、K_P は比例ゲイン、T_I は積分時間（リセットタイム）、T_D は微分時間（レートタイム）という。

位相進み補償器

一巡伝達関数（閉ループ特性）の高周波域のゲインを高め、ゲイン交さ周波数を高周波域へシフトさせることにより、安定性を補償しつつ、速応性を改善できる。

位相補償メモ

制御系の挙動

一巡伝達関数のゲインが低下→フィードバック制御系の即応性低下
安定限界に近づく→振動的になり減衰特性が劣化
定常速度偏差が減少→定常特性が改善
定常速度偏差が増大→定常特性が劣化

特性方程式

　フィードバック制御系の閉回路伝達関数の特性根により制御系の安定性を示すためのもの。一般的なブロック線図において、伝達関数の分母を0とおいた方程式、
F(s)=1+G(s)H(s)=0
F(s)が特性方程式となる。

特性方程式が二次式である場合、この系が安定である条件は以下となる。

• 特性根がともに実根で負の値をとる。（一つでも正の値であれば不安定）
• 特性根が複素根をとるときは、共役の関係にある場合は、振動する形となる。実部が負の値をとる場合は振動は減衰する。実部が零であれば持続振動となる。

特性方程式の判別式（振動判別）

特性方程式　F(s)=s²+as+b=0　において
解の公式より$s=\frac{-a±\sqrt{a^2-4b}}{2}$
したがって、特性方程式の判別式
D=a²-4b<0のとき、特性根は複素共役複となり、制御系は振動する。
同じくD>0では実解、D＝0では重解となる。

ラウス・フルビッツの安定判別法

特性方程式　F(s)=1+G(s)H(s)=0　について
F(s)=a₀s³+a₁s²+a₂s+a₃=0　とおくと、
この系が安定であるための条件は以下を全て満たすこと

1. 全ての係数a₀、a₁、a₂、a₃が存在し、同符号である
2. 下のラウス表の第１列が全て同符号である

	1	2
1	a₀	a₂
2	a₁	a₃
3	b₁=$\frac{a_1a_2-a_0a_3}{a_1}$
4	c₁=$\frac{b_1a_3}{b_1}$=a₃

　上記二つの条件を全て満足するときF(s)の特性根の実部はすべて負となり、系は安定である。

部分分数分解による係数比較法

下式の左辺は右辺のように分解することができる。

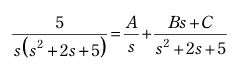
両辺の分母をそろえて払うと

二次遅れ要素の標準形

　二次遅れ要素の標準形は、減衰係数 ζ 、固有角周波数 ω_n[rad/s]とすると、
$\displaystyle G(s)=\frac{ω_n^2}{s^2+2ζω_ns+ω_n^2}$
となる。

　2階線形微分方程式で表される、二次遅れ系システム（振動的な挙動を制御する、フィードバック制御系）の特性を容易に把握できる。

定常速度偏差

　制御偏差の時間応答e(t)について、定常値になったものを定常速度偏差e_vといい、
$\displaystyle e_v=\lim_{t→∞} e(t)=\lim_{s→0}E(s)$
$\displaystyle e_v=\lim_{s→0} E(s)$をラプラス変換の最終値の定理という。

正弦波入力時の定常偏差

　目標値として正弦波を与えたとき、偏差E(s)までの伝達関数を求め、ω=1として、伝達関数の絶対値（ゲイン）を求める。入力正弦波の振幅（波高値）にこのゲインをかけたものが、偏差の振幅になる。例題として、2種2022年機械制御 問4や2種過去問2010年機械制御 問4などがある。

• 電験３種過去問【2023年(前期)機械 問13】(RL回路の周波数伝達関数)
• 電験３種過去問【2022年(後期)機械 問15】（RLC回路の伝達関数とボード線図）
• 電験３種過去問【2022年(前期)機械 問15】（フィードバック制御の一巡伝達関数とベクトル軌跡）
• 電験３種過去問【2021年機械 問13】（周波数伝達関数のボード線図）
• 電験３種過去問【2020年機械 問17】（周波数伝達関数とブロック線図）
• 電験３種過去問【2016年機械 問13】（フィードバック制御における基本的な制御動作）

• 電験２種過去問【2023年機械制御 問4】（古典制御、ゲイン特性、折れ線近似）
• 電験２種過去問【2022年機械制御 問4】（古典制御、特性方程式、安定条件、定常速度偏差）
• 電験２種過去問【2021年機械制御 問4】（古典制御、振動判別、安定判別）
• 電験２種過去問【2018年機械制御 問4】（古典制御、ゲイン特性、２自由度制御）
• 電験２種過去問【2017年機械制御 問4】（古典制御、RLC直列回路、二次遅れ系の導出）
• 電験２種過去問【2011年機械制御 問4】（古典制御、特性方程式、安定条件、補償器）
• 電験２種過去問【2010年機械制御 問4】（古典制御、安定限界、定常偏差、ゲイン特性、位相補償器）
• 電験２種過去問【2009年機械制御 問4】（古典制御、持続振動、定常速度偏差、制御系の挙動）

• 電験１種過去問【2023年機械制御 問4】（古典制御におけるフィードバック制御系の解析）
• 電験１種過去問【2022年機械制御 問4】(古典制御におけるフィードバック制御系の解析)
• 電験１種過去問【2021年機械制御 問4】（古典制御におけるフィードバック制御系の解析）
• 電験１種過去問【2020年機械制御 問4】(古典制御におけるベクトル軌跡を用いたフィードバック制御系の解析)
• 電験１種過去問【2019年機械制御 問4】（古典制御におけるフィードバック制御系の解析）
• 電験１種過去問【2017年機械制御 問4】（古典制御、閉ループ制御系、根軌跡法）
• 電験１種過去問【2014年機械制御 問4】（古典制御におけるフィードバック制御系の解析）
• 電験１種過去問【2012年機械制御 問4】（古典制御におけるフィードバック制御系の解析）
• 電験１種過去問【2011年機械制御 問4】(古典制御におけるフィードバック制御系の解析)
• 電験１種過去問【2009年機械制御 問4】（古典制御におけるフィードバック制御系の解析）

現代制御

　二種二次、一種になると、出題されます。
　詳しい理論はさておき、定義や計算手法をしっかり覚えましょう！

状態空間表現

状態変数を x₁(t)、 x₂(t)、制御対象の入力と出力をそれぞれ u(t)、y(t) とする。このとき、状態ベクトル x(t)=[x₁(t)　x₂(t)]^Tが満たす次の状態空間表現

$\boldsymbol{\dot{x}}(t)=\boldsymbol{Ax}(t)+\boldsymbol{b}u(t) \\y(t)=\boldsymbol{cx}(t)$

における

A=$\begin{pmatrix}a_1&a_2\\a_3&a_4\end{pmatrix}$,b=$\begin{pmatrix}b_1\\b_2\end{pmatrix}$,c=$\begin{pmatrix}c_1&c_2\end{pmatrix}$である。

下記表現と同義。

$\frac{dx_1(t)}{dt}=a_1x_1(t)+a_2x_2(t)+b_1u(t)$

$\frac{dx_2(t)}{dt}=a_3x_1(t)+a_4x_2(t)+b_2u(t)$

固有値と特性多項式

　$\boldsymbol{\dot{x}}(t)$=Ax(t)+bu(t)
　制御入力u(t)=0 のとき、行列 A の固有値を与える特性多項式は
　| sI–A | 　(det[ sI–A ] とも表現する)で与えられる。
　ただし、I は単位行列を表す。

特性方程式と安定性

　特性方程式 | sI–A | = 0　の解（システム行列Aの固有値）が全て負であるとき、制御対象は安定である。

可制御性行列

可制御性行列 U_C = (b　Ab)で与えられるとき、
| U_C | ≠ 0 のとき、制御対象は可制御である。| U_C | = 0 のとき、制御対象は不可制御である。
または、 U_C が2行2列のとき、rank U_C =2であれば、可制御である。

可観測性行列

可制御性行列 U_O が以下で与えられるとき、

$\boldsymbol{U_O}= \begin{bmatrix} \boldsymbol{c}\\ \boldsymbol{cA} \end{bmatrix}$

| U_O | ≠ 0 のとき、制御対象は可観測である。| U_O | = 0 のとき、制御対象は不可観測である。
または、 U_Oが2行2列のとき、rank U_O =2であれば、可観測である。

• 電験２種過去問【2016年機械制御 問4】（現代制御、閉ループ状態方程式、定常偏差）

• 電験１種過去問【2018年機械制御 問4】（現代制御におけるフィードバック制御系の解析）
• 電験１種過去問【2016年機械制御 問4】(現代制御におけるフィードバック制御系の解析)
• 電験１種過去問【2015年機械制御 問4】(現代制御におけるフィードバック制御系の解析)
• 電験１種過去問【2013年機械制御 問4】（現代制御におけるフィードバック制御系の解析）
• 電験１種過去問【2010年機械制御 問4】（現代制御におけるフィードバック制御系の解析）

電験についての関連記事