電験3種過去問【2022年(上期)機械 問15】
【自動制御】フィードバック制御の一巡伝達関数とベクトル軌跡《計算問題》
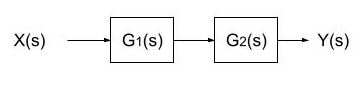
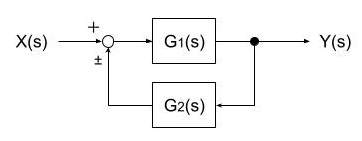
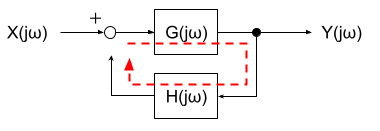
図は、出力信号 y を入力信号 x に一致させるように動作するフィードバック制御系のブロック線図である。次の(a)及び(b)の問に答えよ。

(a) 図において、K = 5 、T = 0.1 として、入力信号からフィードバック信号までの一巡伝達関数(閉ループ伝達関数)を表す式を計算し、正しいものを次の(1)~(5)のうちから一つ選べ。
\displaystyle (1) \frac{5}{1-j\omega 0.1} \displaystyle (2) \frac{5}{1+j\omega 0.1} \displaystyle (3) \frac{1}{6+j\omega 0.1} \displaystyle (4) \frac{5}{6-j\omega 0.1} \displaystyle (5) \frac{5}{6+j\omega 0.1}
(b) (a)で求めた一巡伝達関数において、 ω を変化させることで得られるベクトル軌跡はどのような曲線を描くか、最も近いものを次の(1)~(5)のうちから一つ選べ。
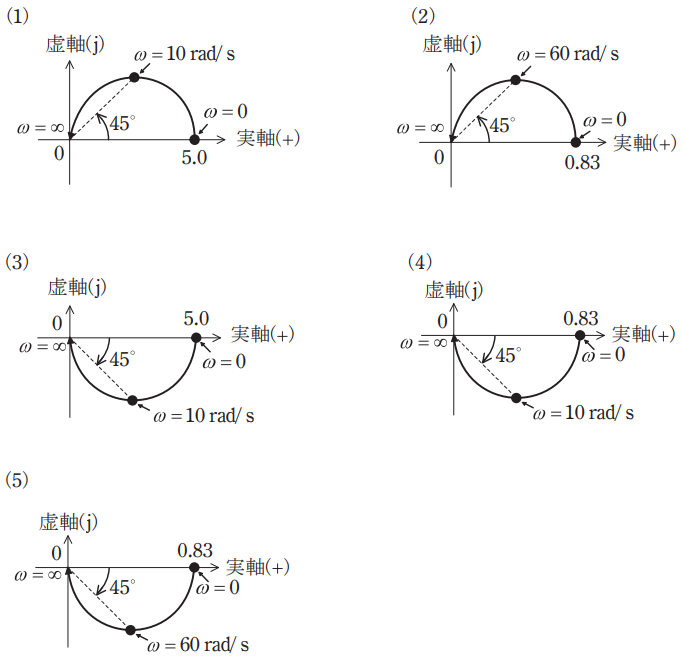

ディスカッション
コメント一覧
まだ、コメントがありません