直流電動機の学習帳
直流機の構造
直流機の構造は、固定子と回転子とからなる。固定子は、界磁、継鉄などによって構成され、また、回転子は、電機子、整流子などによって構成されている。
電機子鉄心は、交番磁束が通るので、交番磁束による渦電流損を少なくするため、電磁鋼板を層状に重ねた積層鉄心が用いられている。また、電機子巻線を収めるための多数のスロットが設けられている。
六角形(亀甲型)の形状の電機子巻線は、そのコイル辺を電機子鉄心のスロットに挿入する。各コイル相互のつなぎ方には、重ね巻と波巻とがある。直流機では、同じスロットにコイル辺を上下に重ねて２個ずつ入れた二層巻としている。
直流機には他励式と自励式がある。自励式には、分巻発電機、直巻発電機などがある。
直流機の電気子反作用
直流発電機や直流電動機では、電機子巻線に電流を流すと、電機子電流によって電機子周辺に磁束が生じ、電機子電圧を誘導する磁束すなわち励磁磁束が、電機子電流の影響で変化する。このように、電機子電流による起磁力がエアギャップの磁束分布に影響を与える作用を電機子反作用という。この影響を防ぐために補償巻線や補極が用いられる。
直流機の界磁磁極片に補償巻線を設け、そこに電機子電流を流すことにより、電機子反作用を緩和できる。大型の機器等で採用される。
直流機の界磁磁極のN極とS極の間に補極を設け、そこに設けたコイルに電機子電流を流すことにより、電機子反作用を緩和できる。
直流電動機に生じる電機子反作用の向きは発電機の場合とは反対であるが、電機子電流の向きが反対であるので補償巻線や補極の接続方法は発電機の場合と同じでよい。
界磁電流による磁束のベクトルに対し、電機子電流による電機子反作用磁束のベクトルは、直交する向きとなるため、交差磁化作用と呼ばれる。この作用により、電動機として運転した場合電気的中性軸の傾き方向は回転方向とは逆方向に傾き、発電機として運転した場合は回転方向へ傾く。
電気的中性軸にブラシの位置を適切に移動させることで、電機子反作用によるブラシに火花が生じる影響を緩和できる。
- 電験３種過去問【2023年(前期)機械 問1】(直流機の構造)
- 電験３種過去問【2022年(後期)機械 問1】（直流機の構造）
- 電験３種過去問【2019年機械 問2】（直流電動機の電機子反作用）
- 電験３種過去問【2012年機械 問1】（直流機の構造）
逆起電力
直流電動機に外部から電圧Vを加えると、電機子電流Iaが流れ、電機子が回転する。このとき、電機子巻線は磁束を切って回転するので、フレミングの右手の法則により電機子巻線には、外部からの直流電圧と逆向きに、つまり電機子電流を減少させる向きに誘導起電力が発生する。この逆向きの誘導起電力を逆起電力という。
逆起電力E[V]は、1極あたりの磁束Φ[Wb]、回転速度ｎ[rpm]とすると次式で表される。
$$E= KΦn$$
直流電動機のトルクと出力
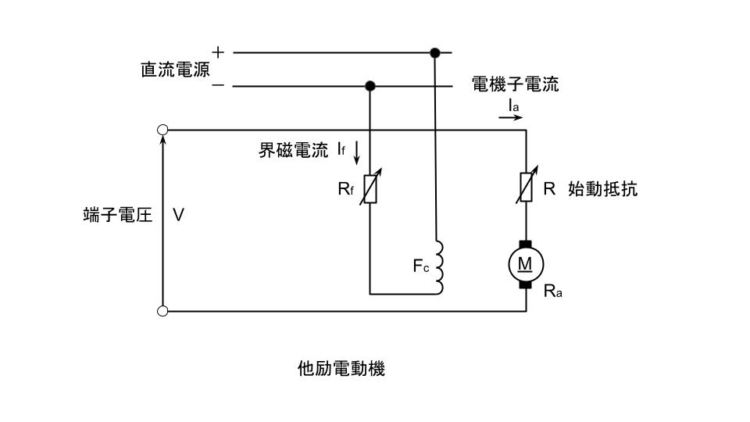
端子電圧V[V]、界磁抵抗Rf[Ω]を一定にすれば、界磁磁束Φ[Wb]は一定であって、電機子電流Ia[A]、電機子抵抗Ra[Ω]とすると、電機子の回転速度ｎ[rpm]は次式で表される。
$$n= \frac{V-R_{a}I_{a}}{KΦ}$$
直流電動機の回転速度は、1極の磁束Φ[Wb]を一定としたとき、端子電圧V[V]に比例する。（電機子抵抗をRa[Ω]は非常に小さいため、電機子電流Ia[A]の影響は無視できる）
電機子巻線の導体総数をZ、並列回路数をa、電機子電流をIa[A]、1極あたりの磁束をΦ[Wb]、極数をｐとすると、電機子を回転させるトルクT[N・m]は次式となる。
$$T= K_1ΦI_a$$
ただし、K1は、\( \displaystyle K_1= \frac{pZ}{2 \pi a} \)であって、電機子の構造から決まる定数となる。直流電動機のトルクは、1極の磁束Φ[Wb]を一定としたとき、電機子電流Ia[A]に比例する。
電機子の半径をr[m]、電機子全体にはたらく力をF[N]とすると、電機子が1回転する間にする仕事W[J]は、
\(\displaystyle W=2\pi rF＝2\pi T\)[J]
直流電動機の回転速度をｎ[rpm]とすると、電機子が1秒間にする仕事、つまり出力Ｐ[Ｗ]は次式となる。
\(\displaystyle P=2\pi \frac{n}{60}T=ωT\)[W]
直流電動機の出力Ｐ[Ｗ]は回転速度ｎ[rpm]とトルクＴ[N・m]の積に比例する。
また、出力P[W]は次式でも表される。
\(\displaystyle P=EI_a\)[W]
- 電験３種過去問【2019年機械 問1】（直流電動機の回転速度とトルク）
- 電験３種過去問【2018年機械 問1】（直流電動機の始動抵抗）
- 電験３種過去問【2015年機械 問1】（直流電動機のトルク）
- 電験３種過去問【2012年機械 問2】（直流電動機の始動抵抗）
- 電験３種過去問【2010年機械 問1】（直流電動機の速度・トルク特性）
- 電験３種過去問【2009年機械 問2】（直流電動機の回転速度）
直流電動機の速度制御法
分巻電動機では始動時の過電流を防止するために始動抵抗が電機子回路に直列に接続されている。
直流電動機の速度制御法には界磁制御法・抵抗制御法・電圧制御法がある。静止レオナード方式は電圧制御法の一種であり、主に他励電動機に用いられ、広範囲の速度制御ができるという利点がある。
直流電動機の回転の向きを変えることを逆転といい、一般的には、応答が早い電機子電流の向きを変える方法が用いられている。
電車が勾配を下るような場合に、電動機を発電機として運転し、電車のもつ運動エネルギーを電源に送り返す方法を回生制動という。
電験３種過去問【2022年(前期)機械 問1】（直流電動機の運転）
他励直流電動機の特徴
直流他励電動機の制御に関する記述である。ただし、鉄心の磁気飽和と電機子反作用は無視でき、また、電機子抵抗による電圧降下は小さいものとする。
- 他励電動機は、界磁電流と電機子電流を独立した電源で制御できる。磁束は界磁電流に比例する。
- 磁束一定の条件で電機子電流を増減すれば、電機子電流に比例するトルクを制御できる。
- 磁束一定の条件で電機子電圧を増減すれば、電機子電圧に比例する回転数を制御できる。
- 電機子電圧一定の条件で磁束を増減すれば、ほぼ磁束に反比例する回転数を制御できる。回転数の上昇のために界磁電流を弱める制御がある。
このように広い速度範囲で速度とトルクを制御できるので、直流他励電動機は圧延機の駆動などに広く使われてきた。
電験３種過去問【2022年(前期)機械 問7】（各種電動機の性質）
電験３種過去問【2020年機械 問1】（直流他励電動機の制御）
電験３種過去問【2014年機械 問1】（直裕電動機のトルク）
電験３種過去問【2013年機械 問1】（直流電動機の特徴）
分巻電動機の特性
負荷トルクに関係なく、回転速度が一定な、定速度電動機である。
分巻電動機は、端子電圧を一定として機械的な負荷を増加したとき、電機子電流が増加し、回転速度は、わずかに減少するがほぼ一定である。このため、定速度電動機と呼ばれる。
上記のように直流分巻電動機の界磁磁束を一定にして運転した場合、電機子反作用を無視すると、トルクは電機子電流にほぼ比例する。
分巻電動機の速度制御の方法の一つとして界磁制御法がある。これは、界磁巻線に直列に接続した界磁抵抗器によって界磁電流を調整して界磁磁束の大きさを変え、速度を制御する方法である。
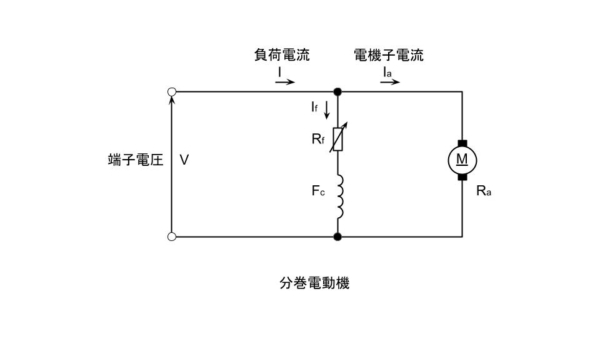
上図において、端子電圧V[V]、界磁抵抗Rf[Ω]を一定にすれば、界磁磁束Φ[Wb]は一定であって、電機子の回転速度ｎ[rpm]は次式で表される。
$$n= \frac{V-R_{a}I_{a}}{KΦ}$$
直巻電動機の特性
直流直巻電動機は界磁回路と電機子回路とが直流に接続されており、界磁磁束は負荷電流によって作られる。界磁磁束が磁気飽和しない領域では、界磁磁束は負荷電流にほぼ比例し、トルクは負荷電流の2乗にほぼ比例する。
直巻電動機は、界磁磁束は電機子電流すなわち負荷電流によってつくられる。界磁磁束が磁気飽和しない、未飽和領域を考えると、界磁磁束Φ[Wb]は、負荷電流I[A]に比例する。したがって、回転速度ｎ[rpm]は次式となる。
$$n= \frac{V-R_{a}I_{a}}{KΦ}= \frac{V-R_{a}I_{a}}{KI}=K’ \frac{V}{I}$$
上式が示すように、回転速度ｎ[rpm]は、負荷電流I[A]の増加に反比例して減少する。このように、直巻電動機は、負荷電流の増減によって回転速度が大きく変わるので、変速度電動機とよばれる。
直巻電動機のトルクは、界磁磁束の未飽和領域を考えると、界磁磁束Φ[Wb]が負荷電流Ｉ[A]に比例するということから次式であらわされる。
$$T= K_1ΦI= K’I^2$$
すなわち、トルクＴ[N・m]は、未飽和領域では負荷電流Ｉ[A]の2乗に比例する。なお、飽和領域では、界磁磁束Φ[Wb]はほぼ一定であるから、トルクＴ[N・m]は、負荷電流Ｉ[A]に比例する。
直巻電動機は、負荷電流の増減によって回転速度が大きく変わる。トルクは、回転速度が小さいときに大きくなるので、始動時のトルクが大きいという特徴があり、クレーン、巻上機などの電動機として適している。
複巻電動機の特性
複巻電動機には、直巻界磁巻線及び分巻界磁巻線が施され、合成界磁磁束が直巻界磁磁束と分巻界磁磁束との和になっている構造の和動複巻電動機と、差になっている構造の差動複巻電動機とがある。
直流電動機の効率
端子電圧V[V]で、負荷電流I[A]が流れると、直流電動機にはPi＝VI[W]の電力が供給される。電動機の機械的出力をPo[W]、損失をPl[W]とすると、効率η[％]は次式で与えられる。
$$η= \frac{P_o}{P_i} \times100= \frac{P_i-P_l}{P_i} \times100 [％]$$
始動抵抗
電機子回路に直列な始動抵抗を接続して電源電圧を加え始動電流を制限する。
過去問題：
電験３種過去問【2021年機械 問1】（分巻・直巻直流電動機の特徴）
電験３種過去問【2021年機械 問2】（分巻電動機の発生トルク）
電験３種過去問【2021年機械 問7】（各種電動機の始動法）
その他の直流モータ
ブラシレスDCモータ
ブラシレスDCモータは、固定子巻線に流れる電流と、回転子に取り付けられた永久磁石によってトルクを発生させる構造となっている。
ブラシレスDCモータは、回転子の位置により通電する巻線を切り換える必要があるため、ホール素子などのセンサによって回転子の位置を検出している。
ブラシ付きの直流モータに比べ、ブラシと整流子による機械的接触部分がないため、火花による電気雑音は低減し、モータの寿命は長くなる。
ブラシ付きの直流モータに比べ、位置センサの信号処理や、駆動用の制御回路が必要となり、モータの駆動に必要な周辺回路が複雑になる。
ブラシレスDCモータは効率がよく、エアコンや冷蔵庫のような省エネ性能が求められる大型の家電製品に利用されている。
ステッピングモータ
- ステッピングモータは、パルスが送られるたびに定められた角度を１ステップとして回転する。
- ステッピングモータは、送られてきたパルスの周波数に比例する回転速度で回転し、入力パルスを停止すれば回転子も停止する。
- ステッピングモータは、負荷に対して始動トルクが大きく、つねに入力パルスと同期して始動できるが、過大な負荷が加わると脱調・停止してしまう場合がある。
- ステッピングモータには、永久磁石形、可変リラクタンス形、ハイブリッド形などがある。永久磁石を用いない可変リラクタンス形ステッピングモータでは、無通電状態では回転子位置を保持する力が働かない。
- ステッピングモータは、回転角度センサーを用いなくても、１ステップごとの位置制御ができる特徴がある。プリンタやスキャナなどのコンピュータ周辺装置や、各種検査装置、製造装置など、様々な用途に利用されている。