電験3種過去問【2018年機械 問1】
【直流機】直流電動機の始動抵抗《計算問題》
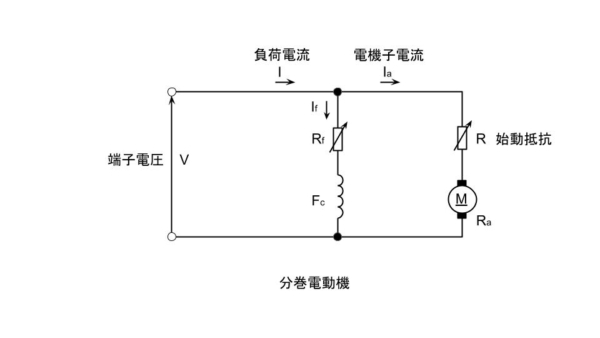
界磁磁束を一定に保った直流電動機において、0.5Ωの抵抗値をもつ電機子巻線と直列に始動抵抗(可変抵抗)が接続されている。この電動機を内部抵抗が無視できる電圧200Vの直流電源に接続した。静止状態で電源に接続した直後の電機子電流は100Aであった。
この電動機の始動後、徐々に回転速度が上昇し、電機子電流が50Aまで減少した。トルクも半分に減少したので、電機子電流を100Aに増やすため、直列可変抵抗の抵抗値をR1[Ω]からR2[Ω]に変化させた。R1及びR2の値の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、ブラシによる電圧降下、始動抵抗を調整する間の速度変化、電機子反作用及びインダクタンスの影響は無視できるものとしする。
| R1 | R2 | |
| (1) | 2.0 | 1.0 |
| (2) | 4.0 | 2.0 |
| (3) | 1.5 | 1.0 |
| (4) | 1.5 | 0.5 |
| (5) | 3.5 | 1.5 |

 https://archivelog.net/denken/
https://archivelog.net/denken/
ディスカッション
コメント一覧
まだ、コメントがありません