対称座標法による故障計算
対象座標法による、各種定義、短絡、地絡故障計算定義、各種等価回路をまとめる。
頭のいい人たちが考えた、不平衡故障をあたかも平衡故障として取り扱うことができる計算法。対象座標法での計算ができないばっかりに、見事不合格となった電験一種二次試験のくやしさを晴らすため、難しい理論はいったん捨て去り、理解のカギとなる項目のみを集めました。
目次
対称座標法の概要
電力系統の故障電流は、故障点にテブナンの定理を適用し、電力系統側を電圧源とインピーダンスからなる等価回路で表現して計算するのが一般的である。その際には、故障点に仮想的に設けた端子での三相電圧・電流を対称座標変換し、故障点から見た電力系統を発電機の基本式を用いて表すことにより故障電流を計算することが多い。
定義
対称座標法では、三相(a, b, c で表す)の電圧・電流を零相、正相、逆相(それぞれ 0, 1, 2 で表す)の電圧・電流に変換する。
各相の電圧と電流をそれぞれ\dot{V}_a,\dot{V}_b,\dot{V}_c,\dot{I}_a,\dot{I}_b,\dot{I}_cとすると、
正相電圧 \dot{V}_1=\displaystyle \frac{1}{3}(\dot{V}_a+a\dot{V}_b+a^2\dot{V}_c)
逆相電圧 \dot{V}_2=\displaystyle \frac{1}{3}(\dot{V}_a+a^2\dot{V}_b+a\dot{V}_c)
零相電圧 \dot{V}_0=\displaystyle \frac{1}{3}(\dot{V}_a+\dot{V}_b+\dot{V}_c)
正相電流 \dot{I}_1=\displaystyle \frac{1}{3}(\dot{I}_a+a\dot{I}_b+a^2\dot{I}_c)
逆相電流 \dot{I}_2=\displaystyle \frac{1}{3}(\dot{I}_a+a^2\dot{I}_b+a\dot{I}_c)
零相電流 \dot{I}_0=\displaystyle \frac{1}{3}(\dot{I}_a+\dot{I}_b+\dot{I}_c)
と定義される。a=e^{j\frac{2}{3}\pi}=1\angle\frac{2}{3}\pi=-\frac{1}{2}+j\frac{\sqrt3}{2}はベクトルオペレータ。
これらの式から逆に各相の電圧、電流を対象分で表すと
a相電圧 \dot{V}_a=\dot{V}_0+\dot{V}_1+\dot{V}_2
b相電圧 \dot{V}_b=\dot{V}_0+a^2\dot{V}_1+a\dot{V}_2
c相電圧 \dot{V}_c=\dot{V}_0+a\dot{V}_1+a^2\dot{V}_2
a相電流 \dot{I}_a=\dot{I}_0+\dot{I}_1+\dot{I}_2
b相電流 \dot{I}_b=\dot{I}_0+a^2\dot{I}_1+a\dot{I}_2
c相電流 \dot{I}_c=\dot{I}_0+a\dot{I}_1+a^2\dot{I}_2
行列式での定義
行列式表記のほうが記憶し易く、計算時もスッキリするのでこちらで覚える!
正相・逆相・零相電圧
\begin{bmatrix} \dot{V}_0 \\ \dot{V}_1 \\ \dot{V}_2 \end{bmatrix} =\displaystyle \frac{1}{3} \begin{bmatrix} 1 & 1 & 1 \\ 1 & α & α^2 \\ 1 & α^2 & α \end{bmatrix} \begin{bmatrix} \dot{V}_a \\ \dot{V}_b \\ \dot{V}_c \end{bmatrix}
正相・逆相・零相電流
三相各相電圧
三相各相電流
各種回路の対称分インピーダンス
対称座標法の計算のためには発電機等の対称分インピーダンスが必要である。発電機、送電線、変圧器の直列インピーダンスは以下の特徴を有する。
発電機の対称分等価回路
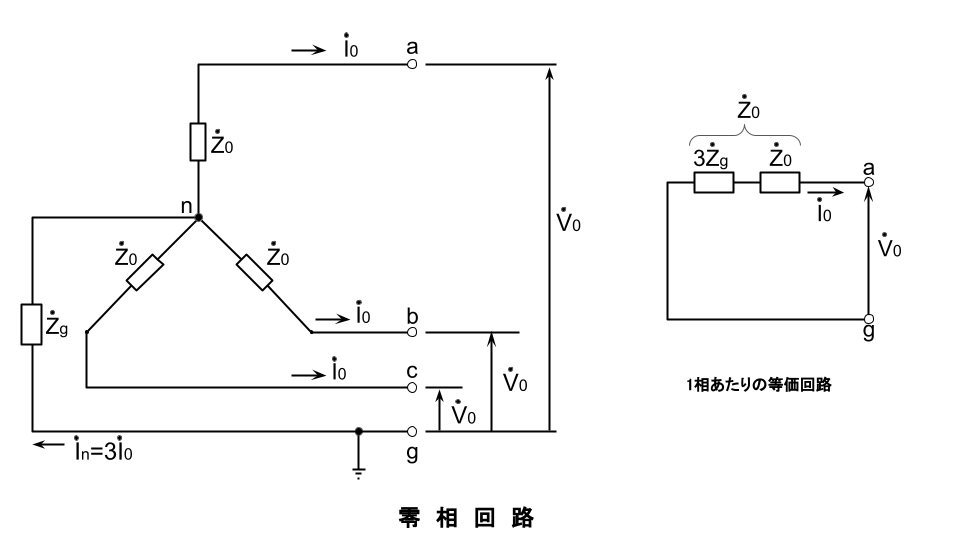
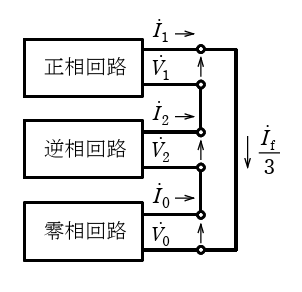
発電機:正相の電機子電流は発電機内に機械的な回転方向と同じ方向に回転する回転磁界を、逆相の電機子電流はそれと反対方向に回転する回転磁界を作るのに対して、零相の電機子電流は発電機内に回転磁界を作らない。これらにより、発電機の零相、正相、逆相インピーダンスは異なる値をとる。図は、単相の外部電源(電圧\dot{V})に発電機の三相巻線を直列に接続することにより、発電機の零相インピーダンスを測定する回路である。この場合、\dot{V}は三相電圧の和となるため零相電圧の3倍となり、電流\dot{I}は三相電流が等しいため零相電流だけとなる。このため、\dot{V}と\dot{I}より零相インピーダンスが求められる。

平衡運転する発電機の、正相分無負荷電圧のみを考える。(逆相分、零相分がないもとする)
a相の無負荷電圧と発電機の零相、正相、逆相インピーダンスをそれぞれ\dot{E}_a,\dot{Z}_0,\dot{Z}_1,\dot{Z}_2とすると、発電機の基本式は、
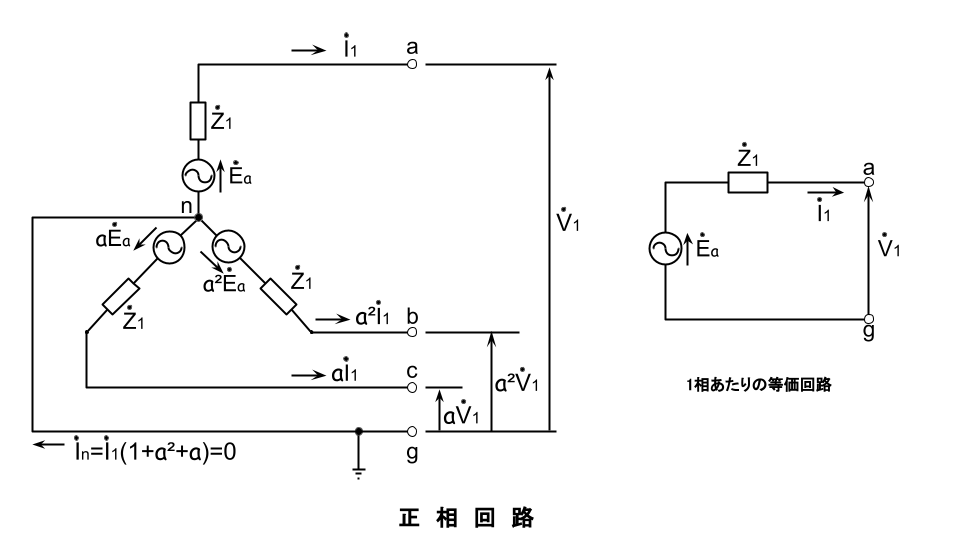
正相電圧 \dot{V}_1=\dot{E}_a-\dot{Z}_1\dot{I}_1
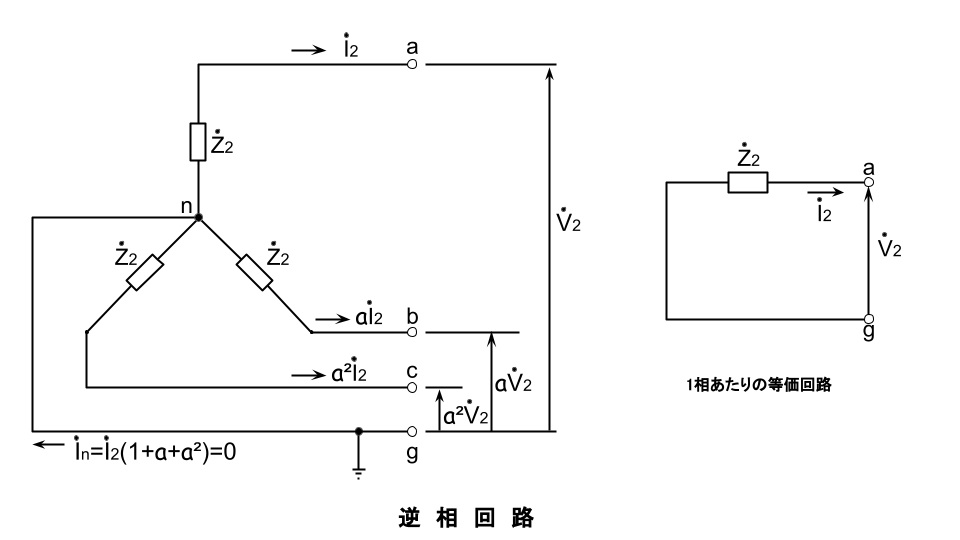
逆相電圧 \dot{V}_2=-\dot{Z}_2\dot{I}_2
零相電圧 \dot{V}_0=-\dot{Z}_0\dot{I}_0
発電機の対称分等価回路はそれぞれ下図となる。
送電線の対称分等価回路
送電線:正相及び逆相電流が作る電線周辺の磁界の大きさはどちらでも同じとなるため、正相及び逆相インピーダンスは同一となる。また、零相インピーダンスは、零相電流が大地を帰路として各相導体に同位相で流れるため、正相、逆相インピーダンスより大きい。
変圧器の対称分等価回路
変圧器:正相、逆相インピーダンスとしては変圧器の漏れリアクタンスを考慮する必要がある。また零相インピーダンスには、変圧器の結線方式とともにその中性点接地インピーダンスが大きく影響する。
変圧器の正相・逆相インピーダンス
変圧器の励磁回路(励磁電流)を無視すれば、変圧器の正相インピーダンス、逆相インピーダンス、漏れインピーダンスをそれぞれ\dot{Z}_1,\dot{Z}_2,\dot{Z}_tとすると
\dot{Z}_1=\dot{Z}_2=\dot{Z}_t
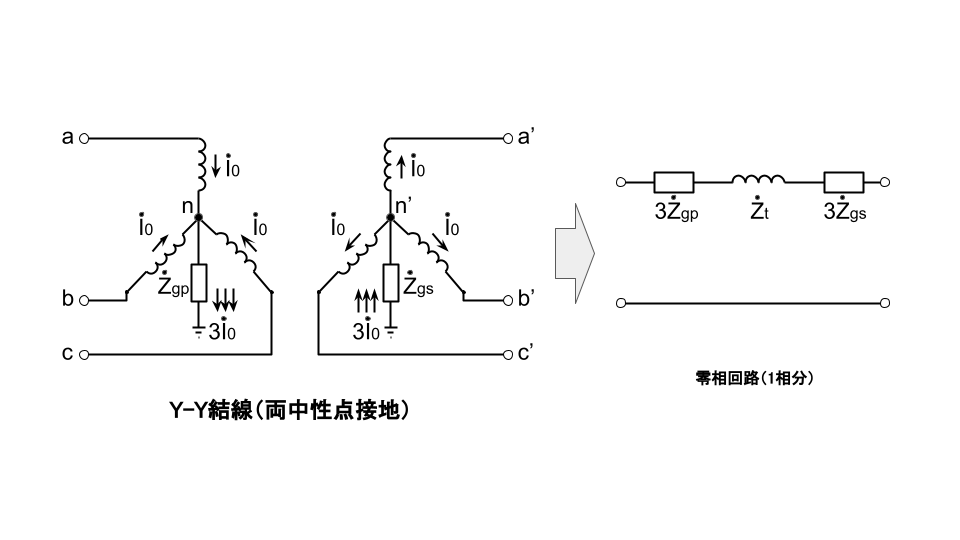
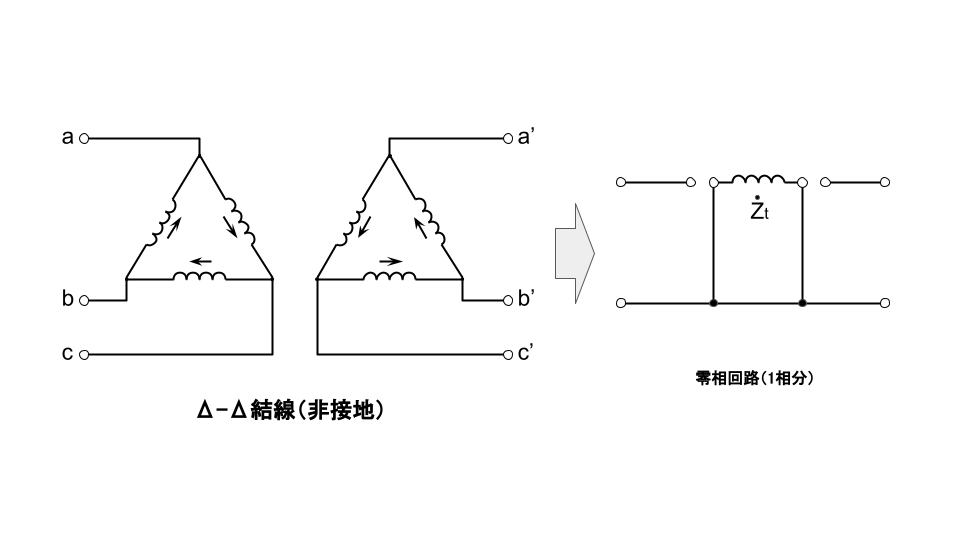
変圧器の零相インピーダンス
変圧器の零相インピーダンスは、結線法と中性点接地方式により異なる。
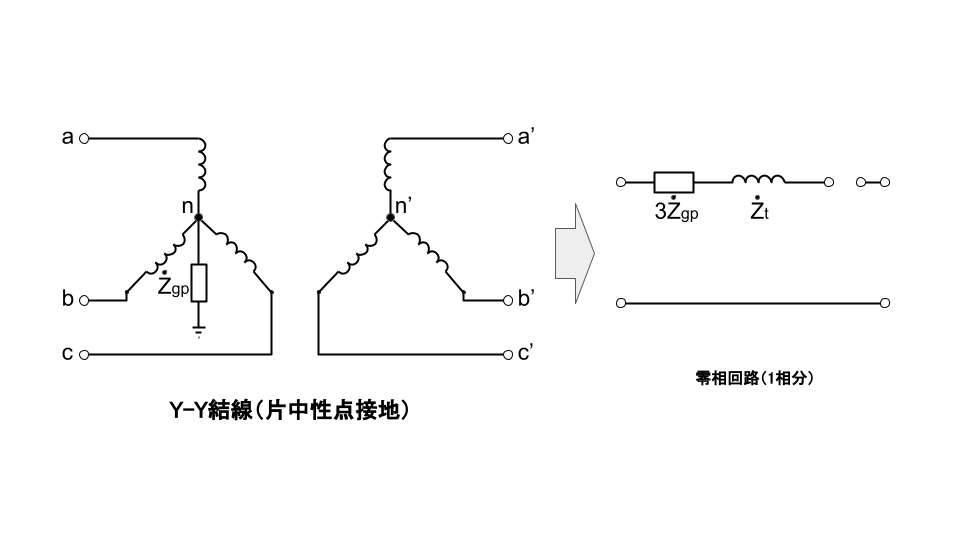
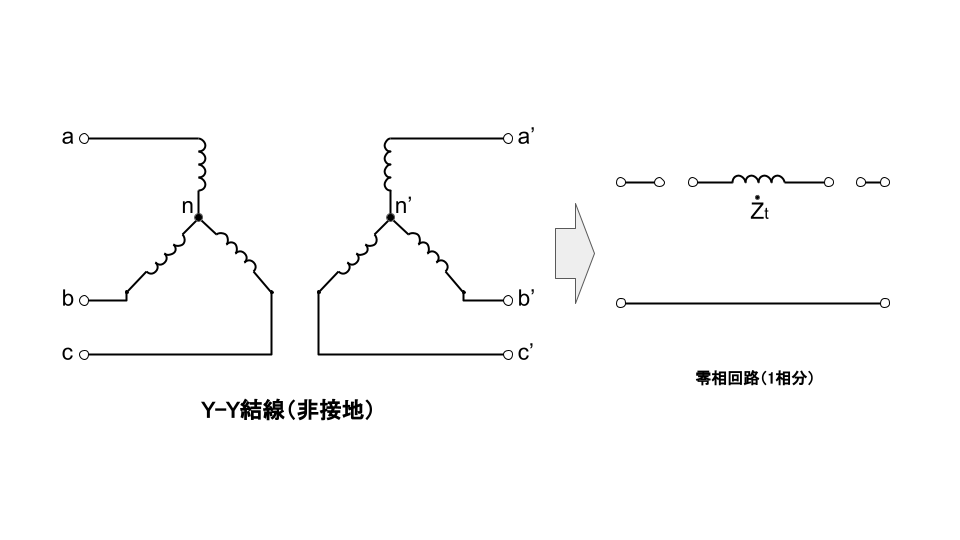
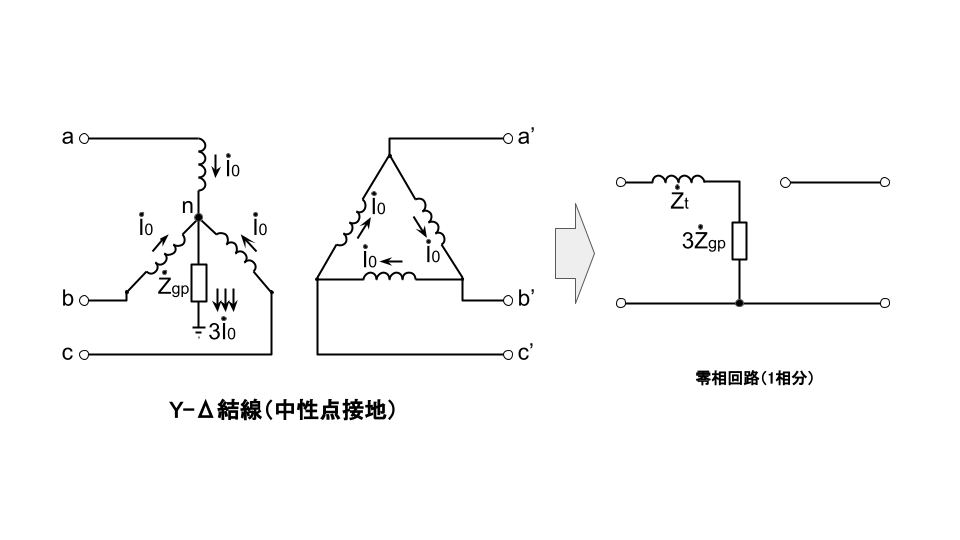
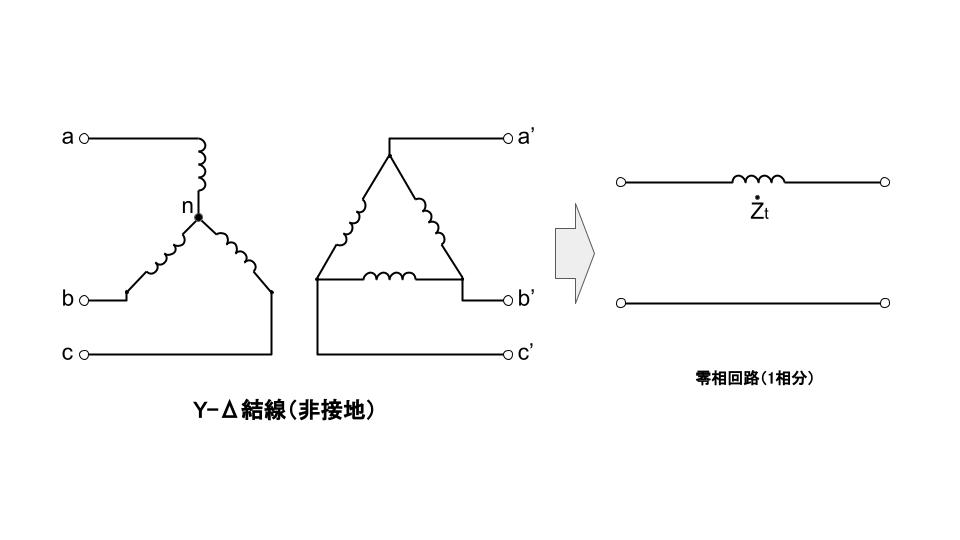
地絡短絡故障計算方法
1線地絡故障
地絡抵抗ありの場合
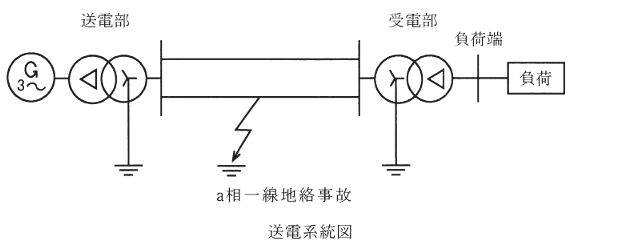
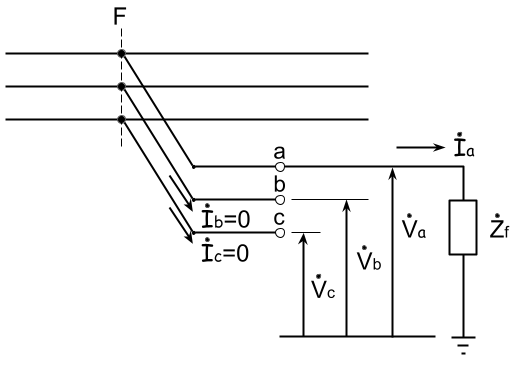
a 相での一線地絡事故を考えると、地絡インピーダンスを\dot{Z}_fとすると、地絡点におけるそれぞれの相の電圧と電流は
\left\{ \begin{array}{l} \dot{V}_a=\dot{I}_a \dot{Z}_f\\ \dot{I}_b=\dot{I}_c=0 \end{array} \right.とおける。
\dot{V}_0,\dot{V}_1,\dot{V}_2をそれぞれ零相、正相、逆相電圧、\dot{I}_0,\dot{I}_1,\dot{I}_2をそれぞれ零相、正相、逆相電流とすると、
相電圧に関して、
\begin{bmatrix} \dot{V}_a \\ \dot{V}_b \\ \dot{V}_c \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 1 & α^2 & α \\ 1 & α & α^2 \end{bmatrix} \begin{bmatrix} \dot{V}_0 \\ \dot{V}_1 \\ \dot{V}_2 \end{bmatrix}より、
\left\{ \begin{array}{l} \dot{V}_a=\dot{V}_0+\dot{V}_1+\dot{V}_2=\dot{I}_a \dot{Z}_f\\ \dot{I}_0=\dot{I}_1=\dot{I}_2=\frac{1}{3}\dot{I}_a \end{array} \right.を得る。
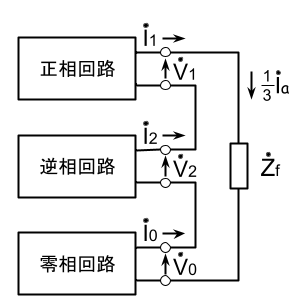
対称座標法における、この条件を満たす回路構成は零相、正相、逆相回路を直列に接続した図となる。また、この直列回路の末端にあらわれる電圧は、
\dot{V}_0+\dot{V}_1+\dot{V}_2=\dot{I}_a \dot{Z}_f=\dot{I}_0 3\dot{Z}_fつまり、等価的に 3\dot{Z}_fがつながった等価回路となる。
地絡抵抗ゼロの場合
下図では a 相での一線地絡事故を考えているため、地絡電流\dot{I}_f=\dot{I}_aである。
実際に問題を解いてみよう!(1線地絡故障)
2線地絡故障
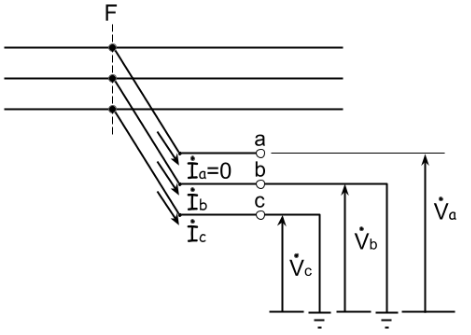
b, c 相での2線地絡事故を考えると、地絡インピーダンスはゼロとすると、地絡点におけるそれぞれの相の電圧と電流は
\left\{ \begin{array}{l} \dot{V}_b=\dot{V}_c=0\\ \dot{I}_a=0 \end{array} \right.とおける。
\dot{V}_0,\dot{V}_1,\dot{V}_2をそれぞれ零相、正相、逆相電圧、\dot{I}_0,\dot{I}_1,\dot{I}_2をそれぞれ零相、正相、逆相電流とすると、
相電流に関して、
\begin{bmatrix} \dot{I}_a \\ \dot{I}_b \\ \dot{I}_c \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 1 & α^2 & α \\ 1 & α & α^2 \end{bmatrix} \begin{bmatrix} \dot{I}_0 \\ \dot{I}_1 \\ \dot{I}_2 \end{bmatrix}より、
\left\{ \begin{array}{l} \dot{I}_a=\dot{I}_0+\dot{I}_1+\dot{I}_2=0\\ \dot{V}_0=\dot{V}_1=\dot{V}_2=\frac{1}{3}\dot{V}_a \end{array} \right.を得る。
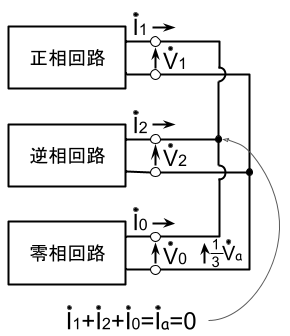
対称座標法における、この条件を満たす回路構成は零相、正相、逆相回路を並列に接続した図となる。また、この並列回路の末端にあらわれる電圧は、
\dot{V}_0=\dot{V}_1=\dot{V}_2=\frac{1}{3}\dot{V}_aとなる。
2相短絡故障

b, c 相での2相短絡事故を考えると、短絡点でのインピーダンスはゼロとすると、短絡点におけるそれぞれの相の電圧と電流は
\left\{ \begin{array}{l} \dot{V}_b=\dot{V}_c\\ \dot{I}_a=0\\ \dot{I}_b=-\dot{I}_c \end{array} \right.とおける。
\dot{V}_0,\dot{V}_1,\dot{V}_2をそれぞれ零相、正相、逆相電圧、\dot{I}_0,\dot{I}_1,\dot{I}_2をそれぞれ零相、正相、逆相電流とすると、
相電流に関して、
\begin{bmatrix} \dot{I}_0 \\ \dot{I}_1 \\ \dot{I}_2 \end{bmatrix} =\displaystyle \frac{1}{3} \begin{bmatrix} 1 & 1 & 1 \\ 1 & α^2 & α \\ 1 & α & α^2 \end{bmatrix} \begin{bmatrix} 0 \\ \dot{I}_b\\ -\dot{I}_b \end{bmatrix}より、
\left\{ \begin{array}{l} \dot{I}_0=0\\ \dot{V}_1=\dot{V}_2=\frac{1}{3}(\dot{V}_a-\dot{V}_b) \end{array} \right.を得る。また、発電機の基本式は、
\left\{ \begin{array}{l} \dot{V}_{0}=-\dot{Z}_{0}\dot{I}_{0}\\ \dot{V}_{1}=\dot{E}_{a}-\dot{Z}_{1}\dot{I}_{1}\\ \dot{V}_{2}=-\dot{Z}_{2}\dot{I}_{2} \end{array} \right.であるので、
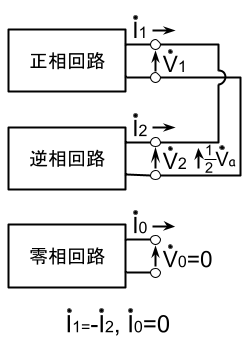
\left\{ \begin{array}{l} \dot{I}_0=0より\\ \dot{V}_{0}=-\dot{Z}_{0}\dot{I}_{0}=0\\ \end{array} \right.を得る。対称座標法における、この条件を満たす回路構成は正相、逆相回路を並列に接続した図となる。零相回路は、零相電圧、零相電流ともにゼロであるため、影響を及ぼさない。また、この並列回路の末端にあらわれる電圧は、
\dot{V}_1=\dot{V}_2=\frac{1}{2}\dot{V}_aとなる。
断線故障計算方法
下図のように、F点で断線故障が発生した場合を考える。3線すべてを開放し、故障点より左のA側およびB側について、それぞれテブナンの等価回路を考える。
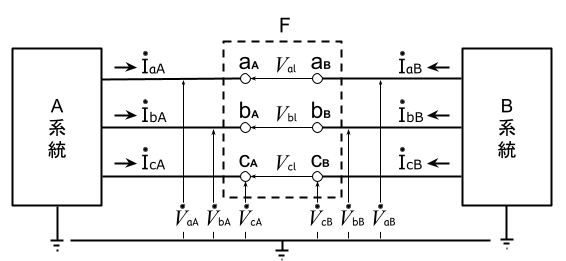
上図の開放端子間の電圧が、
\left\{ \begin{array}{l} \dot{V}_{al}=\dot{V}_{aA}-\dot{V}_{aB}\\ \dot{V}_{bl}=\dot{V}_{bA}-\dot{V}_{bB}\\ \dot{V}_{cl}=\dot{V}_{cA}-\dot{V}_{cB} \end{array} \right.であるから、下式が得られる。
\left\{ \begin{array}{l} \dot{V}_{0l}=\dot{V}_{0A}-\dot{V}_{0B}\\ \dot{V}_{1l}=\dot{V}_{1A}-\dot{V}_{1B}\\ \dot{V}_{2l}=\dot{V}_{2A}-\dot{V}_{2B} \end{array} \right. …(1)また、3線を開放した状態では
\left\{ \begin{array}{l} \dot{I}_{aA}+\dot{I}_{aB}=0\\ \dot{I}_{bA}+\dot{I}_{bB}=0\\ \dot{I}_{cA}+\dot{I}_{cB}=0 \end{array} \right.となるので、電流の対称成分も
\left\{ \begin{array}{l} \dot{I}_{0A}=-\dot{I}_{0B}\\ \dot{I}_{1A}=-\dot{I}_{1B}\\ \dot{I}_{2A}=-\dot{I}_{2B} \end{array} \right.となる。
以上のことから、この回路の開放端子間電圧の零相分、正相分、逆相分電圧\dot{V}_{0l},\dot{V}_{1l},\dot{V}_{2l}は、下図のような、3線を開放した各対称分の等価回路を得られる。
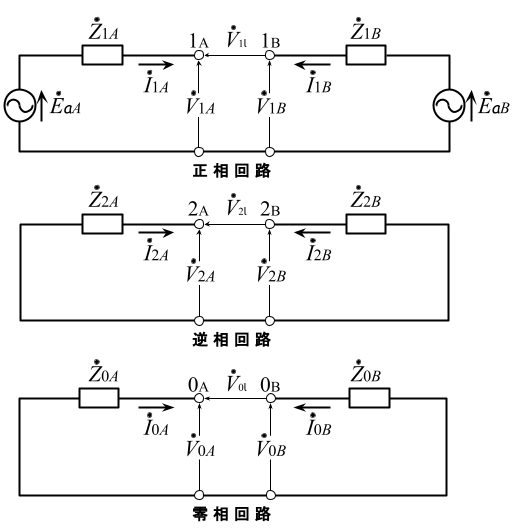
また、発電機の基本式より、A側の基本式は
\left\{ \begin{array}{l} \dot{V}_{0A}=-\dot{Z}_{0A}\dot{I}_{0A}\\ \dot{V}_{1A}=\dot{E}_{aA}-\dot{Z}_{1A}\dot{I}_{1A}\\ \dot{V}_{2A}=-\dot{Z}_{2A}\dot{I}_{2A} \end{array} \right. …(2)B側の基本式は
\left\{ \begin{array}{l} \dot{V}_{0B}=-\dot{Z}_{0B}\dot{I}_{0B}\\ \dot{V}_{1B}=\dot{E}_{aB}-\dot{Z}_{1B}\dot{I}_{1B}\\ \dot{V}_{2B}=-\dot{Z}_{2B}\dot{I}_{2B} \end{array} \right. …(3)式(2),(3)を式(1)に代入すると
\left\{ \begin{array}{l} \dot{V}_{0l}=-(\dot{Z}_{0A}+\dot{Z}_{0B})\dot{I}_{0A}\\ \dot{V}_{1l}=(\dot{E}_{aA}-\dot{E}_{aB})-(\dot{Z}_{1A}+\dot{Z}_{1B})\dot{I}_{1A}\\ \dot{V}_{2l}=-(\dot{Z}_{2A}+\dot{Z}_{2B})\dot{I}_{2A} \end{array} \right.となる。ここで、インピーダンスと開放端子間に流れる電流について
\left\{ \begin{array}{l} \dot{Z}_{0l}=\dot{Z}_{0A}+\dot{Z}_{0B}\\ \dot{Z}_{1l}=\dot{Z}_{1A}+\dot{Z}_{1B}\\ \dot{Z}_{2l}=\dot{Z}_{2A}+\dot{Z}_{2B} \end{array} \right. \left\{ \begin{array}{l} \dot{I}_{0l}=\dot{I}_{0A}=-\dot{I}_{0B}\\ \dot{I}_{1l}=\dot{I}_{1A}=-\dot{I}_{1B}\\ \dot{I}_{2l}=\dot{I}_{2A}=-\dot{I}_{2B} \end{array} \right.のように定義すると、次式のような断線故障の基本式が得られる。
\left\{ \begin{array}{l} \dot{V}_{0l}=-\dot{Z}_{0l}\dot{I}_{0A}\\ \dot{V}_{1l}=\dot{E}_{al}-\dot{Z}_{1l}\dot{I}_{1l}\\ \dot{V}_{2l}=-\dot{Z}_{2l}\dot{I}_{2l} \end{array} \right.ただし、\dot{E}_{al}=\dot{E}_{aA}-\dot{E}_{aB}であり、A側とB側の起電力の差である。
1線断線故障
a相が断線した場合、断線点における線路は下図のようになり、この場合の断線故障の条件式は以下となる。
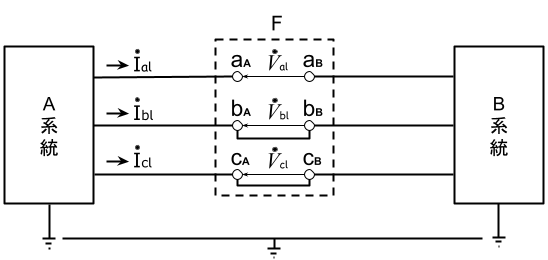
※ちなみに、この条件式は、各々の定義は異なるが、地絡インピーダンスゼロで2線地絡したときの条件と同じである。関連して理解を深めたい場合は、合わせて確認するとよい。
断線点において、\dot{V}_{0l},\dot{V}_{1l},\dot{V}_{2l}をそれぞれ零相、正相、逆相電圧、\dot{I}_{0l},\dot{I}_{1l},\dot{I}_{2l}をそれぞれ零相、正相、逆相電流とすると、
\begin{bmatrix} \dot{V}_{0l} \\ \dot{V}_{1l} \\ \dot{V}_{2l} \end{bmatrix} =\displaystyle \frac{1}{3} \begin{bmatrix} 1 & 1 & 1 \\ 1 & α & α^2 \\ 1 & α^2 & α \end{bmatrix} \begin{bmatrix} \dot{V}_{al} \\ 0 \\ 0 \end{bmatrix}相電流に関して、
\begin{bmatrix} \dot{I}_{al} \\ \dot{I}_{bl} \\ \dot{I}_{cl} \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 1 & α^2 & α \\ 1 & α & α^2 \end{bmatrix} \begin{bmatrix} \dot{I}_{0l} \\ \dot{I}_{1l} \\ \dot{I}_{2l} \end{bmatrix}より、
\left\{ \begin{array}{l} \dot{I}_{al}=\dot{I}_{0l}+\dot{I}_{1l}+\dot{I}_{2l}=0\\ \dot{V}_{0l}=\dot{V}_{1l}=\dot{V}_{2l}=\frac{1}{3}\dot{V}_{al} \end{array} \right.を得る。
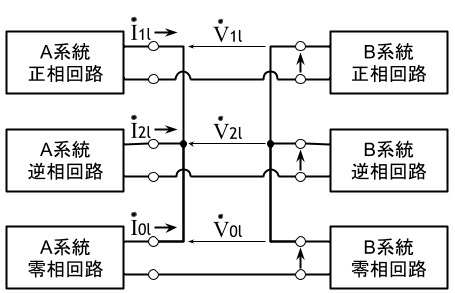
以上より、対称座標法における、この条件を満たす断線故障時の回路構成は零相、正相、逆相回路のA側、B側端子をそれぞれ並列に接続した下図となる。

ディスカッション
コメント一覧
まだ、コメントがありません