電験3種過去問【2016年機械 問1】
【直流機】直流電動機の速度《計算問題》
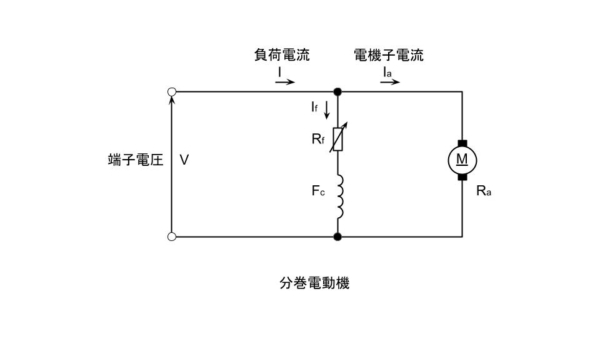
電機子巻線抵抗が0.2Ωである直流分巻電動機がある。この電動機では界磁抵抗器が界磁巻線に直列に接続されており界磁電流を調整することができる。また、この電動機には定トルク負荷が接続されており、その負荷が要求するトルクは定常状態においては回転速度によらない一定値となる。
この電動機を、負荷を接続した状態で端子電圧を100Vとして運転したところ、回転速度は1500min-1であり、電機子電流は50Aであった。この状態から、端子電圧を115Vに変化させ、界磁電流を端子電圧が100Vのときと同じ値に調整したところ、回転速度が変化し最終的にある値で一定となった。この電動機の最終的な回転速度の値[min-1]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、電機子電流の最終的な値は端子電圧が100Vのときと同じである。また、電機子反作用及びブラシによる電圧降下は無視できるものとする。
| (1)1290 | (2)1700 | (3)1730 | (4)1750 | (5)1950 |

ディスカッション
コメント一覧
まだ、コメントがありません