電験２種過去問【2017年機械 問6】

解答

解説

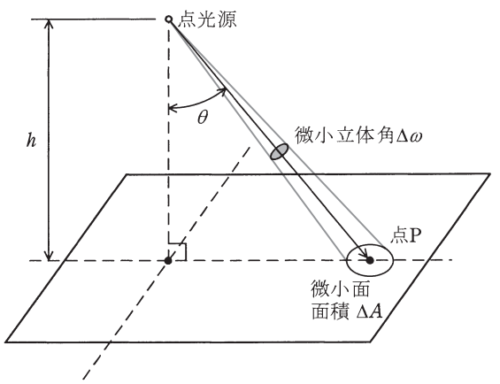
　図のように、点光源が水平な机上面上の高さ$h$にあり、その鉛直角$\theta$方向の微小立体角$\Delta\omega$内を光束$\Phi$が通過している。ここで、点光源とは、光源から照射を受ける面までの距離に比べて、光源の大きさが無視できる程度に小さなものをいう。逆２乗の法則による照度計算は、この点光源を前提としている。
　この条件において、ある点Pの水平面照度$E_h$が、その点Pに対応する微小面の平均照度$E_{av}$であることを以下に説明する。
　まず、光源からある方向に向かう光束の単位立体角当たりの割合を$\fbox{(ﾄ)光度}$という。

　逆２乗の法則による机上面上の点Pの水平面照度$E_h$は、逆２乗の法則に従って、光度$I$、高さ$h$、鉛直角$\theta$を用いて表すと

　$\displaystyle E_h=\frac{I}{l^2}\cos\theta$

ここで、点光源からの距離$l$は$\displaystyle l=\frac{h}{\cos\theta}$であるので、

　$\displaystyle E_h=\frac{I}{(\frac{h}{\cos\theta})^2}\cos\theta$

　$\displaystyle E_h=(ﾊ)\frac{I\cos^3\theta}{h^2}$

となる。点光源の鉛直角$\theta$（点P）方向の光度$I$は、$\Delta\omegaと\Phi$とを用いて表すと$(ｶ)\displaystyle\frac{\Phi}{\Delta\omega}$で求まるので、$hと\theta$が分かれば$E_h$を求めることができる。
　次に、微小立体角$\Delta\omega$が机上面に投影して作る微小面の面積$\Delta A$の平均照度$E_{av}$を求める。照度の定義に従えば、$\Delta A$の平均照度$E_{av}$は$(ﾖ)\displaystyle\frac{\Phi}{\Delta A}$で表せる。

$\Delta A$は微小立体角$\Delta\omega$、高さ$h$、鉛直角$\theta$を用いて表すと

　$\displaystyle \Delta A\cos\theta=\Delta\omega l^2$

ここで、点光源からの距離$l$は$\displaystyle l=\frac{h}{\cos\theta}$であるので、

　$\displaystyle \Delta A=(ﾛ)\frac{\Delta\omega h^2}{cos^3\theta}$

となるので、これを$(ﾖ)\displaystyle\frac{\Phi}{\Delta A}$に代入すれば$E_{av}$を求めることができる。
　この$E_{av}$を求める関係に、$I=(ｶ)\displaystyle\frac{\Phi}{\Delta\omega}$を代入して、$\Phi$、$\Delta\omega$を消去し、光度$I$を用いて表せば$\displaystyle E_h=(ﾊ)\frac{I\cos^3\theta}{h^2}$となる。よって、ある点の水平面照度$E_h$は、その点に対応する微小面の平均照度$E_{av}$と同一である。