同期機の学習帳
目次
三相同期発電機
同期速度
極数が p の同期発電機の同期速度は、
\(\displaystyle n_s=\frac{120f}{p}\)[rpm]
三相同期発電機に発生する誘導起電力
磁束密度の分布が正弦波であれば、各極の磁束 Φ [ Wb ]、周波数を f [ Hz ]、巻線の巻数を w とすれば、1相のコイルに発生する誘導起電力の実効値は
\(\displaystyle E=4.44k_w f\Phi w\)[ V ]
※kwは巻線係数
同期発電機の誘導起電力の発生原理
(ア)誘導起電力e=vblであるので、誘導起電力の瞬時値e(t)は磁束密度の瞬時値b(t)の関数として表せる。すなわち、e(t)=vb(t)lとなる。同時に、e(t)=Emsinωtと定義されているので、
e(t)=Emsinωt=vb(t)l=vBmsinωt l
∴Em=vBm l
ここで、v=2τfであるので、
Em=2τfBm l
(イ)回転磁束が正弦波でその最大値がBmのとき、B=(2/π)Bmで表されるとき、B[T]は平均値である。また、B=(2/√2)Bmで表されるとき、B[T]は実効値である。これは、正弦波の平均値と実効値の定義であるので覚えておく必要がある。
(ウ)1本の導体に生じる起電力の実効値Eは、E=Em/√2=2.22fΦと与えられている。電機子巻線の巻数をNとすると、1巻あたりに起電力を乗じる導体は2本存在するので、1相あたりの誘導起電力はE×N×2=4.44fΦNとなる。
(エ)電機子巻線は一般的には、短節巻や分布巻が採用され、実際に合成された誘導起電力は理想的なものより低くなる。つまり1相あたりの誘導起電力EはE=4.44kWfΦN(kWは1以下)と表され、ここでkWを巻線係数という。
【補足】
分布巻・短節巻での誘導起電力は,集中巻・全節巻で得られる誘導起電力の値に、分布係数と短節係数との積である巻線係数を乗じた値となる。
分布巻の場合の集中巻の場合に対する誘導起電力の大きさの比を分布係数といい、短節巻の場合の全節巻に対する誘導起電力の大きさの比を短節係数という。
集中巻とは、1対のスロットに全ての巻線を巻いたもの。対して分布巻とは複数のスロットにわたり巻線を巻いたもの。
全節巻とは電気角を180°ずらして(2極の場合は物理的に180°相対して)巻線を巻いたもの。対して短節巻とは電気角が180°より小さくなるように巻線を巻いたもの。
同期発電機の励磁方式
小型の同期発電機では界磁に永久磁石を使用することもあるが、中型から大型の同期発電機(以下、主発電機と呼ぶ)では界磁巻線に直流電流を通電して励磁する方法が適用される。
この直流電流(界磁電流)を供給する装置を励磁装置と呼び、近年では交流励磁機方式、又は静止形励磁方式が一般的である。また、この界磁電流の大きさを調整して主発電機の無効電力や端子電圧を調整することを励磁制御という。
交流励磁機方式は、励磁電源として同期発電機を使用しており、この発電機を交流励磁機と呼ぶ。交流励磁機方式では、主発電機の界磁電流の増減は、交流励磁機の界磁電流の調整によって行われる。交流励磁機にも励磁が必要であるが、その電源としてさらに小型の発電機をもう一台使用する場合は、この小型の発電機を副励磁機と呼ぶ。
交流励磁機方式の一つにブラシレス励磁方式がある。ブラシレス励磁方式の交流励磁機の構造は回転電機子形であり、その出力は交流励磁機の回転子と同軸上に設置された半導体電力変換器整流されて、主発電機の界磁巻線に供給される。このため、この方式では主発電機及び交流励磁機に界磁電流を給電するためのスリップリングとブラシが不要である。
静止形励磁方式では、サイリスタ素子を使用した電力変換器を使用する方式が近年一般的であり、サイリスタ励磁方式とも呼ばれる。サイリスタ励磁方式では、その電源を励磁変圧器経由で主発電機の出力回路(主回路)から得る自励方式が多く採用されている。
同期発電機の特性曲線
- 無負荷飽和曲線
同期発電機を定格回転速度、無負荷で運転している場合の界磁電流に対する端子電圧の関係を示す曲線を無負荷飽和曲線という。界磁電流の増加に伴い鉄心が飽和するため、界磁電流と端子電圧の関係は比例関係にならず、いわゆる飽和特性を示す曲線になる。 - 短絡特性曲線
同期発電機の端子を短絡し、定格回転速度で運転した場合の、界磁電流に対する電機子電流の関係を示す曲線を短絡特性曲線という。端子短絡状態では、電機子反作用による減磁作用で界磁起電力の大部分が打ち消されるため界磁電流を増加させても鉄心は磁気飽和せず、特性曲線はほぼ直線となる。
無負荷飽和曲線と短絡特性曲線が得られると、同期発電機の短絡比を求めることができ、この短絡比と単位法(p.u.)で表した同期インピーダンスは互いに逆数の関係になる。 - 負荷飽和曲線
同期発電機を定格回転速度で運転し、電機子電流一定で力率一定の負荷をかけた場合の界磁電流に対する端子電圧の関係を示す曲線を負荷飽和曲線という。負荷飽和曲線のなかで特に電機子電流値が定格で零力率の負荷をかけた場合の曲線を零力率飽和曲線といい、無負荷飽和曲線をポーシェの三角形を用いて平行移動することでもこの飽和曲線を描くことができる。
発電機の出力
Xd [Ω] : 同期リアクタンス、E [V] : 無負荷誘導起電力(相電圧)、V [V] : 端子電圧(相電圧)δ [rad] : 負荷角(内部相差角)
複素電力P+jQ(遅れ力率のときQ>0とする)
\(\displaystyle P+jQ[p.u.]=\frac{VE}{X_s}sinδ+j\frac{VEcosδ-V^2}{X_s}\)
同期発電機の電圧変動率
定格電圧(相電圧)が Vn [p.u.] 、定格電流が In [p.u.] 、 定格力率が cosθn (80%遅れ)、及び同期リアクタンスが Xs である三相円筒形同期発電機に関して、(単位法は自己定格容量及び自己定格電圧を基準とし、電機子抵抗や磁気飽和は無視する)
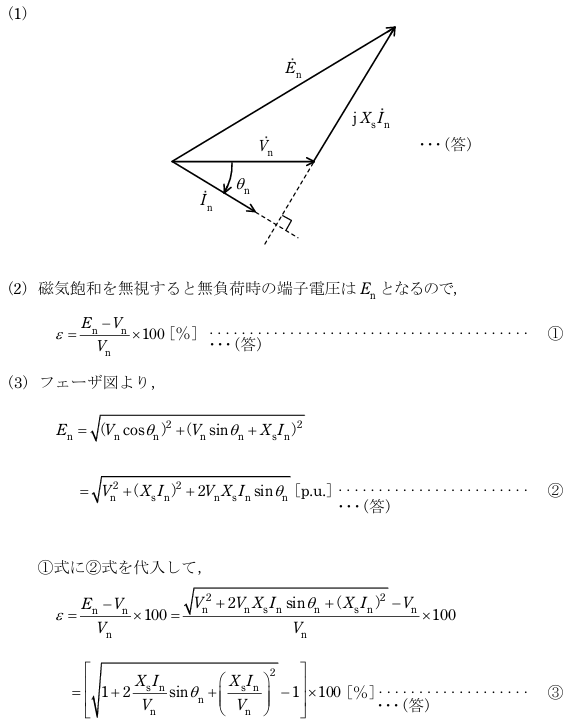
(1)フェザー図を端子電圧(相電圧)を基準にして描くと、
(2)電圧変動率は
(3)電圧変動率εを In 、θn 、 Xs を用いて表すと
同じ発電機でも力率により電圧変動率が異なる理由
➂式に力率遅80%と100%を代入すると、力率80%の方が変動率が大きくなる。
力率が遅れ80%の場合では電機子反作用中に減磁作用成分が含まれるが、力率が100%では電機子反作用は交差磁化作用となる。このため端子電圧を1p.u.にするための界磁電流すなわち無負荷誘導起電力は、力率100%より遅れ力率80%の方が大きくなり、電圧変動率εは遅れ力率80%の場合の方が大きくなる。
- 電験1種過去問【2022年機械制御 問1】(円筒形、フェザー図、電圧変動率導出、力率で変動率が変化する理由)
- 電験1種過去問【2020年機械制御 問1】(円筒形、フェザー図、各種無効電力における界磁電流比較)
同期発電機の系統接続
同期発電機を商用電源(電力系統)に遮断器を介して接続するためには、同期発電機の電圧の大きさ、周波数及び位相が商用電源のそれらと一致していなければならない。同期発電機の商用電源への接続に際しては、これらの条件が一つでも満足されていなければ、遮断器を投入したときに過大な電流が流れることがあり、場合によっては同期発電機が損傷する。仮に、電圧の大きさ、周波数が一致したとしても、位相が異なる場合には位相差による電流が生じる。同期発電機が無負荷のとき、この電流が最大となるのは位相差が180[°]のときである。
同期発電機の電圧の大きさ、周波数及び位相を商用電源のそれらと一致させるためには、電圧調整装置及び調速装置を用いて調整する。
同期発電機の並行運転
ある母線に同期発電機Aを接続して運転しているとき、同じ母線に同期発電機Bを並列に接続するには、同期発電機A、Bの起電力の大きさが等しくそれらの位相が一致していることが必要である。起電力の大きさを等しくするにはBの界磁電流を、位相を一致させるにはBの原動機の回転速度を調整する。位相が一致しているかどうかの確認には同期検定器が用いられる。
並行運転中に両発電機間で起電力の位相が等しく大きさが異なるとき、両発電機間を無効横流が循環する。これは電機子巻線の抵抗損を増加させ、巻線を加熱させる原因となる。
仕様及び特性が等しい2台の三相同期発電機SG1及びSG2を並列接続し、共通の負荷に電力を供給することを考える。速度出力特性がともに等しい垂下特性をもつ原動機で入力を等しく一定として並行運転している場合、両機の間には横流と呼ばれる循環電流は流れない。このとき、各発電機の誘導起電力の大きさ、周波数が等しく、各発電機の誘導起電力の位相がほぼ一致している。この運転状態からSG1の界磁電流を増加すると、両機の誘導起電力に差が生じ、これによって両機の間に循環電流が流れる。この電流はSG1の誘導起電力に対しては遅れ、SG2に対しては進みの無効電流であり、電機子反作用によってそれぞれの磁束に作用して、両機の端子電圧が界磁電流の調整前と比べて高い電圧で平衡を保つように働く。
また、先の並行運転状態において、何らかの原因で一方の発電機の回転速度が一時的に変化し、両機の速度差により誘導起電力の間にわずかな位相差が生じて循環電流が流れたとする。この場合の循環電流は、両機の間で有効電力の授受を行って自動的に両機を同一位相に保つように働く。この場合の循環電流を同期化電流という。
- 電験1種過去問【2024年機械制御 問1】(円筒型同期発電機、並列運転)
- 電験1種過去問【2018年機械制御 問2】(円筒形発電機、無負荷誘導起電力、並列運転)
- 電験1種過去問【2013年機械制御 問2】(円筒形発電機、無負荷誘導起電力、並列運転)
タービン発電機の運動方程式
タービン発電機の回転軸系を一つの質点にて近似した場合、その運動方程式は次式で表される。
J\(\displaystyle\frac{d^2θ_m}{dt^2}\)=Ta [N・m] …➀
ここで、J=\(\frac{GD^2}{4}\) [kg・m²] は慣性モーメント (ただし、GD² [kg・m²] ははずみ車効果) 、θm [rad] は回転子の位置を表す機械角、Ta [N・m] は加速トルク、 t [s] は時間である。
このとき、タービン発電機が回転体としてもつ蓄積エネルギー EK [J] は、
EK=\(\displaystyle\frac{1}{2}J\left(\frac{dθ_m}{dt}\right)^2=\frac{1}{2}\)Jωm² [J] …②
として表される。ここで、ωm [rad/s] は回転子の機械角速度である。
また、➀式の運動方程式は、発電機容量ベースの単位法表現では、タービン発電機の単位慣性定数 H [s] を用いて次のように記述される。
2H\(\displaystyle\frac{d\bar{ω}_e}{dt}=\bar{T}_a\) [p.u.] …③
ここで、\(\bar{ω}_e\) [p.u.] は回転子の電気角速度、\(\bar{T}_a\) [p.u.] は加速トルクである。
回転系の運動エネルギーについてはこちらも
突極形同期発電機モデル
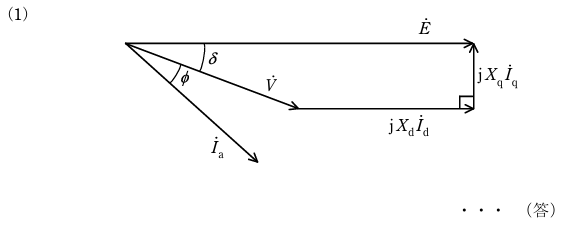
三相星形接続の同期発電機が三相平衡負荷に接続されており、発電機の各定数が以下の記号で示される。
Xd [Ω] : 直軸(d軸)同期リアクタンス、Xq [Ω] : 横軸(q軸)同期リアクタンス、E [V] : 無負荷誘導起電力(相電圧)、V [V] : 端子電圧(相電圧)、Ia [A] : 電機子電流、Id [A] : 電機子電流の直軸(d軸)成分、Iq [A] : 電機子電流の横軸(q軸)成分、φ [rad] : 力率角(遅れ)、δ [rad] : 負荷角(内部相差角)
この同期発電機の電機子巻線抵抗が無視できるとし、遅れ力率で運転しているときのフェザーズは以下。
突極形同期発電機出力
\(\displaystyle P[p.u.]=\frac{VE}{X_d}sinδ+\frac{1}{2}\left(\frac{1}{X_q}-\frac{1}{X_d}\right)V^2sin2δ\)
出力P-負荷角δ曲線
定態安定限界出力における負荷角δmは、
\(\displaystyle \frac{dP}{dδ}=0\)を求めることにより得られる。
三相同期電動機
三相同期電動機が負担を担って回転しているとき、回転子磁極の位置と、固定子の三相巻線によって生じる回転磁界の位置との間には、トルクに応じた角度δ[rad]が発生する。この角度δを負荷角という。
回転子が円筒形で2極の三相同期電動機の場合、トルクT[N・m]はδがπ/2[rad]のときに最大値になる。さらにδが大きくなると、トルクは減少して電動機は停止する。同期電動機が停止しない最大トルクを脱出トルクという。
また、同期電動機の負荷が急変すると、δが変化し、新たなδ’に落ち着こうとするが、回転子の慣性のために、δ’を中心として周期的に変動する。これを乱調といい、電源の電圧や周波数が変動した場合にも生じる。乱調を抑制するには、始動巻線も兼ねる制動巻線を設けたり、はずみ車を取り付けたりする。
三相同期電動機の入力、出力、トルク
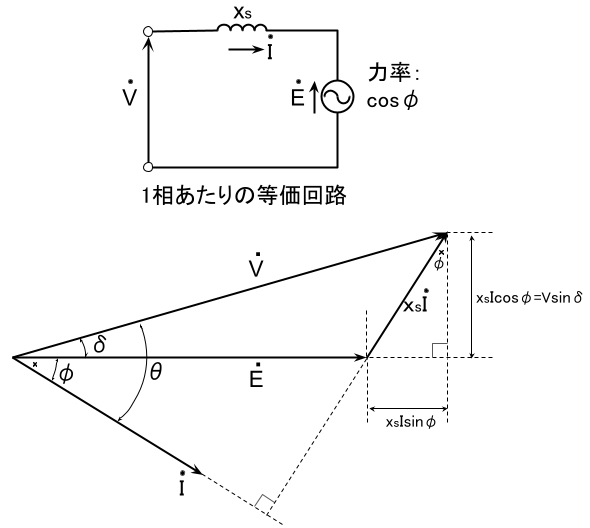
上図の三相同期電動機の1相分の誘導起電力\(E\)[V]、電圧\(V\)[V]、電流\(I\)[A]、\(V\)と\(I\)の位相差を\(\theta\)[rad]としたときの1相分の入力\(P_i\)[W]は次式で表される。
\(P_i=VI\cos\theta\)
また、\(E\)と\(V\)の位相差を\(\delta\)[rad]とすると、1相分の出力\(P_o\)[W]は次式で表される。\(E\)と\(V\)の位相差\(\delta\)は負荷角といわれる。
\(P_o=EI\cos(\delta-\theta)=EI\cos(-\phi)\)
\(=EI\cos\phi\) ∵通常\(\phi\)は90°より小さい
上図より、\(\displaystyle \cos\phi=\frac{V}{x_sI}\sin\delta\)であるので、
\(\displaystyle P_o=\frac{VE}{x_s}\sin\delta\)
ここで\(x_s\)[Ω]は同期リアクタンスであり、電機子巻線抵抗は無視できるものとする。
全出力\(P=3P_o\)[W]は、負荷角\(\sin\delta\)に従って、\(\delta=\frac{\pi}{2}=90°\)のとき最大となる。
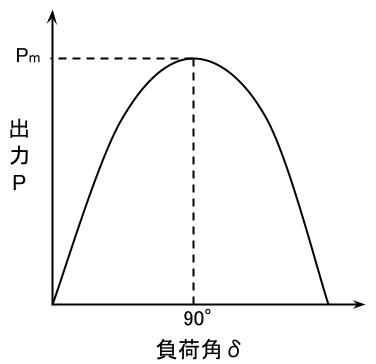
この三相同期電動機の全出力を\(P\)[W]、同期速度を\(n_s\)[min-1]とすると、トルク\(T\)[N・m]とPの関係は次式で表される。
\(\displaystyle P=3P_o=2\pi\frac{n_s}{60}T\)
これから、\(T\)は次式のようになる。
\(\displaystyle T=\frac{60}{2\pi n_s}・3P_o=\frac{60}{2\pi n_s}・\frac{3VE}{x_s}\sin\delta\)
以上のことから、\(\displaystyle 0≦\delta≦\frac{\pi}{2}\)の範囲において\(\delta\)が大きくなるに従って\(T\)は大きくなり、理論上\(\displaystyle \frac{\pi}{2}\)[rad]のとき最大値となる。
同期インピーダンスと百分率同期インピーダンス
定格出力P[V・A]定格線間電圧\(V_n\)[V]、短絡電流\(I_s\)[A]とすると、1相分の同期インピーダンス\(Z_s\)[Ω]は
\(\displaystyle Z_s=\frac{\frac{V_n}{\sqrt3}}{I_s}\) [Ω]
百分率同期インピーダンス\(z_s’\)[%]は次式で定義する。
\(\displaystyle z_s’=\frac{I_n}{I_s}\times100\)[%]
または
\(\displaystyle z_s’=\frac{I_n}{I_s}\)[p.u.]
\(\displaystyle z_s’=\frac{PZ_s}{V_n^2}\)[p.u.]
短絡比Kは
\(\displaystyle K=\frac{1}{z_s’}\)[p.u.]
短絡比が小さいということは、相対的に同期インピーダンスが大きいということになる。
同期インピーダンスが大きいと
- 銅機械(巻線が多い)となる。※逆に短絡比が大きいと鉄機械(鉄心が多い)となり外形寸法や重量大となる
- 発電機出力が小さくなるので、安定度が低下する
- 同期インピーダンスによる電圧降下が大きくなるので、電圧変動率は大きくなる
- 電験3種過去問【2023年(前期)機械 問5】(三相同期発電機の短絡比)
- 電験3種過去問【2022年(後期)機械 問5】(三相同期発電機の短絡比)
- 電験3種過去問【2022年(前期)機械 問5】(三相同期発電機の短絡比)
- 電験3種過去問【2020年機械 問5】(同期電動機の誘導起電力)
- 電験3種過去問【2013年機械 問6】(三相同期発電機の同期インピーダンスの値)
三相同期電動機の始動法
同期電動機は始動のときに回転子を同期速度付近まで回転させる必要がある。一般的な三相同期電動機の始動方法としては以下がある。
自己始動法
自己始動法では、回転子の磁極面に施されている制動巻線を利用して、始動トルクを発生させる。制動巻線は誘導電動機の二次巻線(かご形回転子導体)と同じ働きをして始動トルクを発生させ、同期速度付近に達したとき、界磁巻線に直流励磁を与えて、引入れトルクによって同期化する。
始動時には、回転磁束により界磁巻線に高電圧を誘導し、その絶縁破壊の恐れがあるため、適当な抵抗を通じて界磁巻線を短絡しておく必要がある。この始動法の場合、定格電圧、定格周波数の電源電圧を直接加えて始動する全電圧始動(大きな始動電流が流れる)と、始動時に始動電流を抑制するために、始動補償器、直列リアクトル、始動用変圧器などを用い、電動機電機子電圧を低減して始動する低減電圧始動がある。
始動電動機法
主機と同軸に設備した小形の始動電動機(誘導電動機や直流電動機)を用いて、無負荷状態で、これに直結した三相同期電動機を回転させ、同期速度付近まで加速する。次に、同期電動機の界磁巻線を励磁し同期発電機として、三相電源との並列運転状態を実現する。そののち、始動用電動機の電源を遮断して同期電動機として運転する。この方法は主に大容量機に採用されている。
始動電動機として誘導機を用いる場合は、主機よりも2~4極程度極数が少ないものが使われる。
低周波始動法
低周波始動法は、始動用電源として可変周波数の電源を使用し、定格周波数の25~30%の周波数で同期化し、その後、定格周波数まで周波数を上昇させてから主電源に同期電源を投入する方法である。
永久磁石同期電動機
モータの固定子がつくる回転磁界中に、永久磁石を付けた回転子を入れると、回転子は回転磁界と同じ速度で回転する。これが永久磁石同期モータの回転原理である。
同期電動機の回転子(界磁)は電磁石が一般的であるが、界磁に永久磁石を用いたもの(永久磁石同期電動機。以下、PMモータという)と回転子が鉄心のみで構成されたもの(リラクタンスモータ)もある。PMモータは、回転子に永久磁石を配置しているため、電磁石を用いる方式に比べて励磁装置が必要なく、かご形誘導電動機と同様にシンプルな構造となる。
PMモータは回転子への磁石の配置方法により、表面磁石形(SPM)と埋込磁石形(IPM)の二種類に分けられる。SPMは磁石の磁束を有効活用できるので高トルクでトルクリプルの少ないモータであり、可変速ドライブを行う場合に制御性、応答性の良いモータである。しかし、高速回転時に磁石の剥がれや飛散の可能性があり、構造上の対策を必要とする。
一方IPMは磁石が回転子鉄心内部にあるので、構造的に小型化・高速化に適している。回転子鉄心は高速回転時の磁石を保護しているだけでなく、その構造によってリラクタンストルクも得られ、運転速度領域を広くとれる利点がある。しかしその反面、磁石の磁束の有効活用の面ではSPMに比べ劣り、磁極位置によるトルクリプルも増加する。
リラクタンストルクは、固定子と回転子の鉄心(電磁鋼板)との間に働く回転力のことである。この回転力のみを利用したリラクタンスモータは、永久磁石形同期モータに比べて、材料コストが低いという特徴がある。
PMモータは近年発達の著しいネオジム合金等の希土類永久磁石を用いることで小形・軽量となる利点があることから、家庭用機器、OA機器、電気自動車などに多く用いられてきたが、最近では小型軽量であること活かし鉄道車両用の大出力機への開発も進められている。
PMモータの可変速運転は、可変電圧・可変周波数の電力変換装置と組み合わせて構成される。このうち高性能な精密可変速運転を目的とするベクトル制御では回転子の角度を検出し1台のインバータで1台のPMモータを駆動するのが原則となる。
三相同期電動機の位相特性(V曲線)

図は同期電動機の位相特性曲線を示している。形がVの字のようになっているのでV曲線とも呼ばれている。横軸は界磁電流、縦軸は電機子電流で、負荷が増加するにつれ曲線は上側へ移動する。図中の破線は、各負荷における力率1の動作点を結んだ線であり、この破線の左側の領域は遅れ力率、右側の領域は進み力率の領域である。
図は三相同期電動機の位相特性曲線の一例である。形がVの字のようになっているのでV曲線とも呼ばれている。同期電動機は、界磁電流を変えると、電機子電流の端子電圧に対する位相が変わり、さらに、電機子電流の大きさも変わる。
横軸は界磁電流、縦軸は電機子電流で、負荷が増加するにつれ(電動機の出力を大きくするにつれて)曲線は、C → B → Aの順に上側へ移動する。図の曲線は最低点は力率が1となる点で、図中の破線は、各負荷における力率1の動作点を結んだ線であり、この破線の左側の領域は遅れ力率、右側の領域は進み力率の領域である。
この位相特性を利用して、三相同期電動機を需要家機器と並列に接続して無負荷運転し、需要家機器の端子電圧を調整することができる。このような目的で用いる三相同期電動機を同期調相機という
同期機の運転特性
同期電動機は、定常運転時において、負荷の大小にかかわらず、極数と電源周波数とで定まる同期速度で回転する交流機であり、一般に定速度電動機として用いられる。同期電動機が一定の負荷にて定速運転を行っているとき、界磁電流を増加させると電機子電流の位相は界磁電流増加前よりも進み方向に変化し、減少させると逆方向に変化する。これにより、運転力率を任意に調整することができる。
同期電動機を原動機で駆動すれば、同期発電機として動作させることができる。電機子電流及び端子電圧の大きさ並びに回転速度及び回転方向は電動機運転時と変えず、同期発電機として遅れ力率で運転する場合の界磁電流は、遅れ力率で運転していた同期電動機の界磁電流より大きい。
同期電動機は、インバータ電源などを用いて電源周波数を制御することによって可変速運転を行うことができる。一般に、誘導起電力は回転速度に比例して増減する。したがって、回転速度を定格速度より低くする場合、電源電圧と電源周波数との比を一定に維持するように制御を行えば、磁束をほぼ一定に保つことができる。
永久磁石同期電動機で速度制御を行う場合、高速領域で誘導起電力が電源電圧より高くなり、そのままでは回転速度を上げることができなくなるときがある。このような場合に、電機子電流の位相を進み方向に制御し、電機子反作用によって磁束を弱めるようにすれば、運転領域を高速側に拡大することができる。
交流機の電機子巻線法
電機子巻線法には、1相のコイルをいくつかのスロットに分けて配置する分布巻と、集中巻がある。分布巻の場合、各極各相のスロット数は2以上となる。
分布巻において、コイルピッチを極ピッチよりも短くした巻線法を短節巻と呼ぶ。この巻線法を採用すると、誘導起電力は低くなるが、コイル端を短くできることや、電圧波形が改善できるなどの利点があるため、一般的によく用いられている。

ディスカッション
コメント一覧
まだ、コメントがありません