三相誘導電動機の特性
誘導電動機として広く使用される、三相誘導電動機の各種特性についてまとめます。重要単元です。その他の誘導電動機の種類等についてはこちらのページにまとめます。
目次
三相誘導電動機の基本特性
三相誘導電動機の誘導起電力とトルクの発生
三相誘導電動機で固定子巻線に電流が流れると回転磁界が生じ、これが回転子巻線を切るので回転子巻線に起電力が誘導され、この起電力によって回転子巻線に電流が流れることでトルクが生じる。この回転子巻線の電流によって生じる起電力を打ち消すように固定子巻線に電流が流れる。
回転子が停止しているときは、固定子巻線に流れる電流によって生じる回転磁界は、固定子巻線を切るのと同じ速さで回転子巻線を切る。このことは原理的に変圧器と同じであり、固定子巻線は変圧器の一次巻線に相当し、回転子巻線は二次巻線に相当する。回転子巻線の各相には変圧器と同様に二次誘導起電力を生じる。
回転子が回転しているときは、電動機の滑りを s とすると、二次誘導起電力の大きさは、回転子が停止しているときの s 倍となる。
固定子の励磁電流による同期速度の回転磁界と回転子との速度の差(相対速度)によって回転子に電圧が発生し,その電圧によって回転子に電流が流れる。
トルクは回転子の電流と磁束とで発生するので,トルク特性を制御するため,巻線形誘導機では回転子巻線の回路をブラシとスリップリングで外部に引き出して二次抵抗値を調整する方式が用いられる。
回転子の回転速度が停止 (滑り s=1) から同期速度 (滑り s=0) の間,すなわち,1>s>0 の運転状態では,磁束を介して回転子の回転方向にトルクが発生するので誘導機は電動機となる。回転子の速度が同期速度より高速の場合,磁束を介して回転子の回転方向とは逆の方向にトルクが発生し,誘導機は発電機となる。
三相誘導電動機の滑り周波数と発生トルク
巻線形三相誘導電動機の二次端子を開放した状態で、一次巻線に一定周波数\(f_1\)の三相正弦波交流電圧を印加すると、励磁電流は流れるが、二次電流が流れないので回転子は回転しない。二次端子を短絡すると二次電流が流れ、これと一次電流により発生する回転磁界とによって、回転子にトルクが発生し、回転子は回転し始める。
回転子が滑り\(s\)で回転している場合、同期速度を\(n_0\)とすれば回転子の回転速度は\((1-s)n_0\)で表され、このとき、二次巻線に発生する起電力の周波数\(f_2\)は\(sf_1\)である。\(f_2\)を滑り周波数という。
回転子に負荷を接続し、その負荷を増大させると回転速度は低下する。すなわち、滑りは増加することになり二次巻線に発生する起電力が大きくなる。その結果、二次電流が増加し、負荷トルクと平衡するだけの大きさのトルクを発生する。
定格負荷時は,無負荷時より低速度あり,その差は小さい。このことから三相かご形誘導電動機は定速度電動機と称することができる。
三相誘導電動機の同期回転速度
三相誘導電動機の同期回転速度 ns [min⁻¹]は、電源の周波数を f [Hz]、極数を p とすると次式で与えられる。
三相誘導電動機の滑り
誘導電動機の同期回転速度 ns [min⁻¹]と回転子速度 n [min⁻¹]が同じであると、回転子に対して磁束は動いていないことになる。つまり、誘導電動機を回転させるためのトルクも生じない。実際の誘導電動機では同期回転速度 ns [min⁻¹]よりも回転子の回転速度 n [min⁻¹]は遅くなる。ns に対する ns と n の差は滑りとよばれ s で表される。
三相誘導電動機の回転数
すべりを s とすると、電動機の回転速度 n [min⁻¹]は、
三相誘導電動機の簡易等価回路
三相誘導電動機の等価回路
誘導電動機の一次回路には同期速度の回転磁界,二次回路には同期速度の s 倍の回転磁界が加わる。したがって,一次回路と二次回路の巻数比を 1 とした場合,二次誘導起電力の周波数及び電圧は一次誘導起電力の s 倍になる。
s が小さくなると,二次誘導起電力の周波数及び電圧が小さくなるので,二次回路に流れる電流が小さくなる。この変化を電気回路に表現するため,誘導電動機の等価回路では,二次回路の抵抗の値を \(\frac{1}{s}\) 倍にして表現する。
誘導電動機の等価回路では,一次巻線の漏れリアクタンス,一次巻線の抵抗,二次巻線の漏れリアクタンス,二次巻線の抵抗,及び電動機出力を示す抵抗が直列回路で表されるので,電動機の力率は 1 にはならない。
誘導電動機の等価回路を構成するリアクタンス値及び抵抗値は,電圧が変化しても s が一定ならば変わらない。s 一定で駆動電圧を半分にすれば,等価回路に流れる電流が半分になり,電動機トルクは電圧(電流)の二乗に比例し,4分の1となる。
同期速度と電動機トルクとで計算される同期ワット(二次入力)は,二次銅損と電動機出力との和となる。
三相誘導電動機の1相分等価回路
一次負荷電流I1‘=I2/α(二次電流I2、一次巻線と二次巻線の巻数比α)
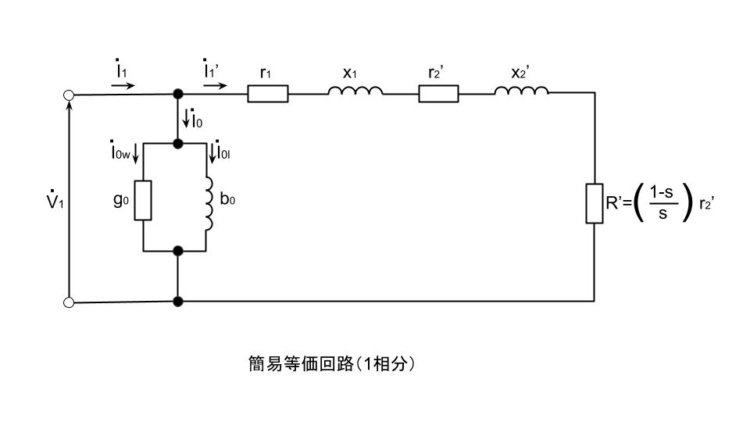
図は、三相誘導電動機の1相分のL形等価回路である。ただし、
\(r_1\)は一次巻線抵抗、
\(r_2’\)は二次巻線抵抗の一次換算値、
\(x_1\)は一次漏れリアクタンス、
\(x_2’\)は二次漏れリアクタンスの一次換算値、
\(b_0\)は励磁サセプタンス、
\(g_0\)は励磁コンダクタンス
である。
三相交流電源の相電圧の実効値を\(V_1\)、フェーザを\(\dot{V_1}\)とする。また、滑りを\(s\)とし、漏れリアクタンスの和を\(X=x_1+x_2’\)とする。
電動機を交流電源に接続すると、励磁電流は\(\dot{I_0}=\dot{Y}\dot{V_1}\)となり、アドミタンス\(\dot{Y}=g_0-jb_0\)であるので
となる。\(\dot{I_0}\)による損失は\(g_0\)を流れる電流となるので、鉄損は
である。機械損\(W_m\)を無視すると、機械的出力(軸出力)\(P_o\)は、二次出力\(P_{o2}\)と等しいので、
である。ここで、
であるので、
である。一方、\(r_1及びr_2’\)に生じる損失は\(W_c=3I_1’^2(r_1+r_2′)\)であるので、
となる。
二次入力
二次銅損
二次出力
二次入力\(P_2\)と二次出力\(P_{o2}\)及び二次銅損\(P_{c2}\)の比
二次入力\(P_2\)と二次出力\(P_{o2}\)及び二次銅損\(P_{c2}\)の比は次の関係となる。
すなわち
誘導電動機の効率
誘導電動機の一次入力\(P_i\)[W]は、一次銅損を\(P_{c1}\)とすると、
\(P_i=W_i+P_{c1}+P_{c2}+P_{o2}\)
一次入力を\(P_i\)とすれば、機械損\(W_m\)を無視すると、電動機の効率 η は
となる。二次出力\(P_{o2}\)及び機械出力(軸出力)\(P_{o}\)、機械損\(P_{m}\)は次の関係となる。
機械損\(W_m\)を考慮した場合、電動機の効率 η は
かご形誘導電動機では、回転子の導体に用いる棒の材料を銅から銅合金に変更すれば、等価回路の二次抵抗の値が増大するので、定格負荷時の効率が低下する。
- 電験3種過去問【2024年(下期)機械 問4】(三相誘導電動機の二次銅損計算)
- 電験3種過去問【2022年(後期)機械 問2】(三相誘導電動機の軸出力)
- 電験3種過去問【2020年機械 問15】(三相誘導電動機の出力)
- 電験3種過去問【2018年機械 問3】(誘導電動機の二次電流)
- 電験3種過去問【2019年機械 問3】(誘導電動機の二次銅損と効率)
- 電験3種過去問【2016年機械 問4】(誘導電動機の同期ワット)
- 電験3種過去問【2017年機械 問3】(誘導電動機のトルクとすべり)
- 電験3種過去問【2017年機械 問15】(誘導電動機の効率と比例推移計算)
- 電験3種過去問【2012年機械 問4】(三相誘導電動機の効率計算)
かご形誘導電動機の等価回路定数測定
三相かご形誘導電動機の等価回路定数測定は様々なかたちで出題される重要単元です。理解してしまえば決して難しいものではありませんし、実務上も重要な試験方法といえます。
等価回路としては一次換算した一相分の簡易等価回路(L型等価回路)が扱われます。回路を覚えて書けるようになっても損はないくらい重要です。(ちなみに、変圧器の等価回路と同じです)
一次巻線抵抗測定
一次巻線の抵抗測定では、静止状態において直流で行う。電動機の一次巻線の各端子間で測定した測定値の平均値から、基準巻線温度における一次巻線の抵抗値を決められた数式を用いて計算する。
巻線抵抗値を換算するための基準巻線温度は絶縁材料の耐熱クラスによって定められており、75℃や115℃などの値が用いられる。
無負荷試験
励磁回路のサセプタンスは無負荷試験により求められる。
無負荷試験では、電動機の一次巻線に定格周波数の定格一次電圧を印加して無負荷運転し、一次側において電圧[V]、電流[A]及び電力[W]を測定する。
拘束試験
一次二次の合成漏れリアクタンスと二次抵抗は拘束試験により求められる。
拘束試験では、電動機の回転子を回転しないように拘束して、一次巻線に定格周波数の低電圧を加えて、全負荷電流に近い電流を流し、一次側において端子電圧[V]、電流[A]及び電力[W]を測定する。
- 電験3種過去問【2022年(前期)機械 問7】(各種電動機の性質)
- 電験3種過去問【2022年(前期)機械 問2】(三相誘導電動機の拘束試験と始動電流)
- 電験3種過去問【2020年機械 問3】(かご形誘導電動機の等価回路定数測定)
三相誘導電動機のトルク
電動機のトルクT[N・m]、角速度ω[rad/s]、回転速度n[rpm]とすれば、出力Po[W]は次式となる。
つまり
Po=(1-s)P2、n=ns(1-s)を代入すると
\(P_{o}= \frac{2 \pi n}{60} T[W]\)はトルクT[N・m]を発生して回転速度n[rpm]で回転しているときの電力をあらわす。
これに対して、\(P_{2}= \frac{2 \pi n_s}{60} T[W]\)は同じトルクT[N・m]の負荷で、同期速度ns[rpm]で回転しているときの出力電力をあらわしている。これを同期ワットと呼ぶ。
同期ワット=二次入力 P₂ [W]
誘導電動機のトルクT[N・m]は、同期ワットP2[W]に比例するので、トルクをあらわすときは出力Po[W]よりも、同期ワットP2[W]で表すことが多い。このときのトルクと同期ワットの関係は次式となる。
- 電験3種過去問【2023年(前期)機械 問4】(三相誘導電動機のトルク計算)
- 電験3種過去問【2015年機械 問15】(巻線形誘導電動機の回転速度変化とトルク計算)
- 電験3種過去問【2014年機械 問4】(三相かご形誘導電動機の電流計算)
- 電験3種過去問【2013年機械 問4】(巻線形誘導電動機の出力計算)
トルク対速度曲線
トルク-回転速度曲線は,電源電圧及び電源周波数が一定のとき,発生するトルクと回転速度との関係を表したものである。この曲線は,ある滑りの値でトルクが最大となる特性を示す。このトルクを最大トルク又は停動トルクと呼んでいる。この最大トルクは二次回路の抵抗には無関係である。
電動機と負荷の特性を、回転速度を横軸、トルクを縦軸に描く、トルク対速度曲線で考える。電動機と負荷の二つの曲線が、どのように交わるかを見ると、その回転数における運転が、安定か不安定かを判定することができる。
負荷トルクよりも電動機トルクが大きいと回転は加速し、反対に電動機トルクよりも負荷トルクが大きと回転は減速する。回転速度一定の運転を続けるには、負荷と電動機のトルクが一致する安定な動作点が必要である。
かご形誘導電動機は、回転トルクが小さい時点から回転速度を上昇させるとともにトルクが増大、最大トルクを超えるとトルクが減少する。
この電動機に回転速度でトルクが変化しない定トルク負荷を接続すると、電動機と負荷のトルク曲線が2点で交わる場合がある。
この場合、速度上昇とともにトルクが減少する領域で負荷トルクが交わる点が安定な動作点である。速度上昇とともにトルクが増大する領域で負荷トルクが交わる点は不安定な動作点である。
かご形誘導電動機は、最大トルクの速度より高速な領域では回転速度の上昇とともにトルクが減少する。一方、送風機のトルクは、回転速度の上昇とともにトルクが増大する。したがって、かご形誘導電動機は、安定に送風機を駆動することができる。
トルクの比例推移
誘導電動機のトルクは二次回路の抵抗と滑りの比に関係するので,二次回路の抵抗が k 倍になると,前と同じトルクが前の滑りの k 倍の点で起こる。このような現象は比例推移と呼ばれ,巻線形誘導電動機の始動特性の改善及び速度制御に広く用いられている。
二次巻線抵抗 r₂’ [Ω]において滑り s であるとき、負荷トルクが一定であれば、二次巻線抵抗 r₂’ [Ω]を 2 倍とすれば、滑り s も 2 倍となる。 r₂’ [Ω]を 3 倍とすれば、滑り s も 3 倍となる。
つまり、二次巻線抵抗 r₂’ [Ω]を k 倍とすれば、滑り s も k 倍となり、次式の関係となる。
\(\displaystyle \frac{r_2′}{s}=\frac{kr_2′}{ks}\)
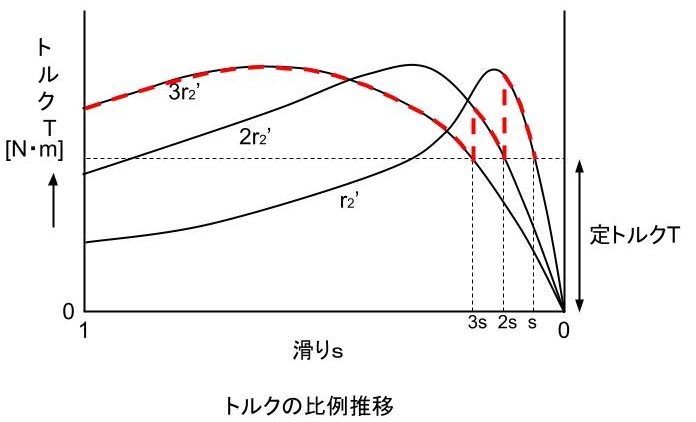
トルク T が一定であれば、すべり s は常に r₂’ [Ω]に比例して推移するので、この変化を比例推移という。
- 電験3種過去問【2024年(下期)機械 問3】(巻線形誘導電動機のトルク速度曲線)
- 電験3種過去問【2017年機械 問15】(誘導電動機の効率と比例推移計算)
- 電験3種過去問【2015年機械 問15】(巻線形誘導電動機の回転速度変化とトルク計算)
トルクに関する問題
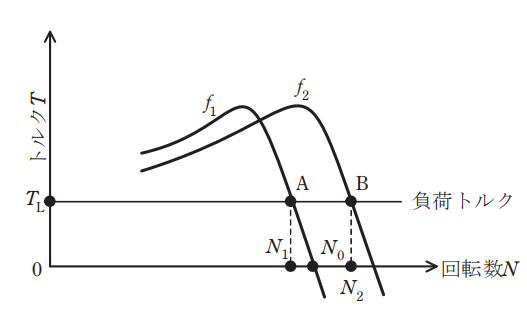
三相誘導電動機の速度制御としてPWMインバータを用いたV/f一定制御が広く用いられている。ここで、Vは電動機の端子電圧、fは端子電圧の周波数である。V/f一定制御されている誘導電動機の定常状態のトルク特性が、端子電圧の周波数\(f_1,f_2\)に対し、図のように与えられている。また、負荷のトルク特性は回転数Nに関わらず\(T_L\)一定で図のように与えられている。このとき、電動機の回転数はそれぞれ、\(N_1,N_2\)である。今、この電動機が\(f_2\)にて運転中で、回転数が\(N_2\)のときに、周波数\(f_1\)に切り換え、\(N_1\)まで減速して、点Aで負荷トルクと電動機トルクがつりあう。
\(N_2\)からの減速過程のうち、\(N_0<N<N_2\)では電動機は発電機動作をするので、電動機は負のトルクを発生する。これにより減速する回転系としては、軸受の摩擦などを無視すると、この発電機動作のトルクと負荷トルクの合成が減速トルクとなる。
続いて、\(N=N_0\)まで減速すると、このとき、電動機は同期速度で運転しているので、負荷トルクのみが減速トルクとなる。
さらに減速して、\(N_1<N<N_0\)となると、電動機は電動機動作をするので、正のトルクを発生する。この区間では電動機の発生トルクは負荷トルクより小さいので、負荷トルクから電動機トルクを差し引いた差が減速トルクとして働く。
- 電験1種過去問【2017年機械制御 問1】(かご形誘導電動機のトルクと滑り計算)
- 電験1種過去問【2015年機械制御 問1】(かご形誘導電動機のトルク比例推移と所要出力計算)
- 電験1種過去問【2013年機械制御 問1】(三相誘導電動機のトルク計算)
三相誘導電動機の始動法
三相誘導電動機の始動においては,十分な始動トルクを確保し,始動電流は抑制し,かつ定常運転時の特性を損なわないように適切な方法を選定することが必要である。その選定のために一般に考慮される特徴の幾つかを述べる。
かご形誘導電動機の始動法
三相かご形誘導電動機は,一次回路を調整して始動する。具体的には,始動時は Y 結線,通常運転時は Δ 結線にコイルの接続を切り替えてコイルに加わる電圧を下げて始動する方法,始動補償器を電源と電動機の間に挿入して始動時の端子電圧を下げる方法,及びインバータを用いて電圧と周波数の両者を下げる方法がある。
全電圧始動法
全電圧始動法は,直入れ始動法とも呼ばれ,かご形誘導電動機において電動機の出力が電源系統の容量に対して十分小さい場合に用いられる。始動電流は定格電流の 5 ~ 8 倍程度の値となる。
三相かご形誘導電動機を全電圧始動した場合、この始動電流によって電動機に関連する設備に次のような問題が生じる可能性がある。
- 過大な始動電流のため大きな電圧降下を生じる。
- 過大な始動電流のためブレーカの動作を招く。
- 電動機への配線の焼損の可能性がある。
- 始動電流に対応するため定格設備容量より過大な設備容量が必要となる。
- 始動時の機械的ショックが大きい。
- 始動電流値に対する保護機器を選定すると適切な保護機能が得られない。
二重かご形誘導電動機は,回転子に二重のかご形導体を設けたものであり,始動時には電流が外側導体に偏り始動特性が改善されるので,普通かご形誘導電動機と比較して大きな容量まで全電圧始動法を用いることができる。
Y-Δ始動法
Y-Δ 始動法は,一次巻線を始動時のみ Y 結線とすることにより始動電流を抑制する方法である。Δ結線の一次巻線をY結線に接続を変えて電源電圧を加え始動電流を制限する。回転速度が上昇するとΔ結線に戻す。
定格出力が 5 ~ 15 kW 程度のかご形誘導電動機に用いられる
Y結線始動時はΔ結線始動時に比べて,始動電流は\(\frac{1}{3}\)に抑えられるが,同時に始動トルクは Δ 結線における始動時の\(\displaystyle \frac{1}{3}\)倍となる。
スターデルタ始動方式を用いて始動電流を低減させた場合の問題点として次のようなものがある。
- 始動トルクが約\(\frac{1}{3}\)に低下するため適用できる負荷が限られる。
- 始動トルクが低下するので始動時間が長くなる。
- スターからデルタに切り換える際に過大な突入電流が生じることがある。
- 切り換え時の電源位相によっては突入電流により、ブレーカの動作を招く。
- 切り換え時の無電圧時間は電動機が空転するためデルタ投入時に機械的ショックを生じる。
Y-Δ始動時のトルク
誘導電動機の発生トルクは入力電圧の2乗に比例する。定格電圧を V [V] とすると,Y 結線始動では,誘導電動機の 1 相にかかる電圧は\(\frac{1}{\sqrt{3}}V\)となる。一方,Δ 結線での全電圧始動では,誘導電動機の 1 相にかかる電圧は V [V] となる。
誘導電動機の Y 結線始動トルクを TY [N・m] とすると,Δ 結線での全電圧始動トルク TΔ [N・m] との比は,
\(\displaystyle \frac{T_Y}{T_Δ}=\frac{\left(\frac{1}{\sqrt{3}}V\right)^2}{V^2}\\ =\displaystyle \frac{1}{3}\)
となる。
Y-Δ始動時の電流
スターデルタ始動方式は、電動機の各相の巻線を、始動時にはスター結線とすることによって相電圧が\(\frac{1}{\sqrt3}\)となり、始動終了後デルタ結線に切り換えることによって電源電圧を各相に供給する方式である。スター結線時はデルタ結線と比較して電源から見た見かけ上のインピーダンスが3倍となるので、線電流が\(\frac{1}{3}\)となる。
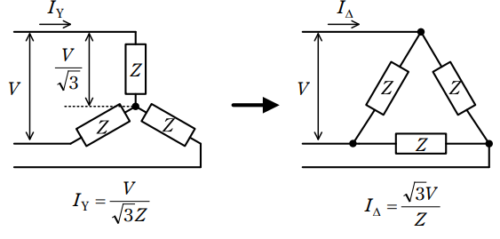
または、このようにも理解できる。スター結線時は相電圧は線間電圧の\(\frac{1}{\sqrt3}\)となるので、線電流も\(\frac{1}{\sqrt3}\)となる。デルタ結線時の線電流は相電流の\(\sqrt3\)倍となる。両者の比をとると、スター結線時の線電流はデルタ結線時の\(\frac{1}{3}\)となる。
始動補償器法
始動補償器法は,三相単巻変圧器を用い,使用する変圧器のタップを切り換えることによって低電圧で始動し運転時には全電圧を加える方法であり,定格出力が 15 kW 程度より大きなかご形誘導電動機に用いられる。
インバータ始動法
インバータ始動法は、インバータを用いて、周波数及び電圧を制御して始動し、定格速度まで連続的に加速する方式である。
インバータを用いて、電動機の一次周波数を最低周波数から定格値まで順次上昇させ、電動機の同期速度を連続的に変えて加速するので、次のような優位な点がある。
- 通常は\(\frac{V}{f}\)を基本とし、電圧特性に補正を施した制御を行うので低周波定電圧でも磁束が低下せず始動トルクが低下しない。
- 始動電流が定格電流の2倍程度以下になる。
- 始動時間をインバータによって制御できる。
- 始動期間に生じる電動機の損失が少なく、発熱を抑制できる。
- ソフトスタートにより始動による機械的ショックが小さい。
- 始動電流や突入電流による他の機器への影響が少ない。
巻線形誘導電動機の始動法
三相巻線形誘導電動機は,二次回路を調整して始動する。
巻線形誘導電動機の始動においては,始動抵抗器を用いて始動時に二次抵抗を大きくすることにより始動電流を抑制しながら始動トルクを増大させる方法がある。具体的には,二次回路をスリップリングで引き出して抵抗を接続し,二次抵抗値を定格運転時よりも大きな値に調整する。
これは誘導電動機のトルクの比例推移特性を利用して,トルクが最大値となる滑りを 1 付近になるようにするものである。
- 電験3種過去問【2023年(下期)機械 問4】(誘導電動機のY-Δ始動トルク計算)
- 電験3種過去問【2018年機械 問4】(三相誘導電動機の始動方法)
- 電験3種過去問【2011年機械 問2】(誘導電動機の始動に関する記述)
誘導電動機の速度制御
電動機の速度制御
誘導機の回転速度n[min-1]は、滑りs、電源周波数f[Hz]、極数pを用いて\(n= \frac{120f(1-s)}{p} [min^{-1}]\)と表される。したがって、誘導機の速度は電源周波数によって制御することができ、特にかご形誘導電動機においてVVVF(Variable Voltage Variable Frequency:可変電圧可変周波数)電源装置を用いた制御が広く利用されている。
かご形誘導機ではこの他に、運転中に固定子巻線の接続を変更して極数を切り換える制御法や、一次電圧の大きさを変更する制御法がある。前者は、効率は良いが、速度の変化が段階的となる。後者は、速度の安定な制御範囲を広くするために二次抵抗の値を大きくとり、銅損が大きくなる。
巻線型誘導機では、二次抵抗の値を調整することにより、トルクの比例推移を利用して速度を変える制御法がある。
- 再電験3種過去問【2023年(下期)機械 問3】(誘導電動機の速度制御)
- 再電験3種過去問【2019年機械 問4】(誘導電動機の速度制御)
- 電験3種過去問【2023年(下期)機械 問15】(誘導電動機の周波数制御時の滑り計算)
誘導電動機の速度を自由に、かつ広範囲に制御できれば、回転機の可変速制御を必要とする分野で広く応用できる。ここに誘導電動機の同期角速度を\(\omega_{s},極数を2p,\)滑りをs,電源周波数をfとすると、回転角速度\(\omega_{m}\)は、次式のように表現される。
\(\omega_m=\omega_s(1-s)=\displaystyle\frac{2\pi f}{p}(1-s)\) …①
①式より、極数、滑りあるいは周波数のいずれかを変化できれば、誘導電動機の速度は制御できることになる。
極数を変化させる方法はあらかじめ極数が変更できるように巻線の接続法を工夫しておき、必要に応じてスイッチで切り換えることにより変える方法であるが、段階的な制御であり連続した可変速を必要とする用途には不向きである。
滑りを変化させる方式では、誘導電動機の発生トルクが入力電圧の2乗に比例することを利用する一次電圧制御法がある。
本方式は滑りの増加とともに電動機の効率が悪化するので、電動機の効率を重視する用途には不向きである。
周波数を連続的に制御する方式は、近年の自励式インバータ電源(電力変換器)による駆動が可能となったことにより広く採用されるようになった。例えばオープンループ制御のインバータ電源による駆動ではV/f一定制御が行われ、電動機の磁束が飽和しないようにしている。さらに精密な回転機の制御が求められる時には、ベクトル制御による高精度制御が行われる。

ディスカッション
コメント一覧
まだ、コメントがありません