誘導電動機の学習帳
目次
- 誘導電動機の回転原理
- 三相誘導電動機の各種特性 →重要単元なので詳細はこちらの別ページ
- 三相誘導電動機の種類
- 単相誘導電動機
誘導電動機の回転原理
アラゴの円板
広く知られている、アラゴの円板を例に回転原理を説明する。下図のようなアルミニウムの円板に回転軸を取り付けたものに、磁石を円板に触れないように近づける。この磁石を矢印の向きに動かすと、円板も磁石と同じ向きに力を受ける。したがって、円板の軸は、磁石の移動する向きと同じ方向へ回転する。
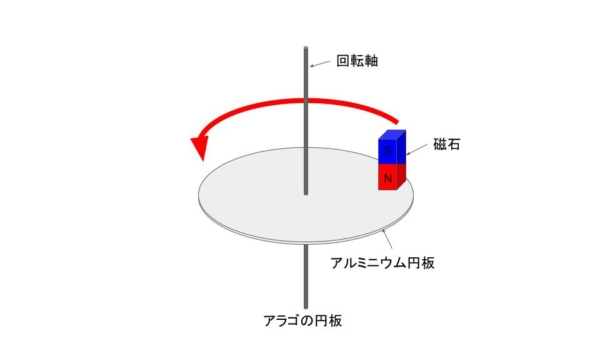
実際の電動機では、磁石を回転させたのと同じ効果があるように工夫がされている。
三相誘導電動機の回転原理
２極の三相誘導電動機に発生する回転磁界
三相交流の回転磁界を作るには、下図のように3つのコイル（赤色のaコイル、緑色のbコイル、青色のcコイル）を互いに120°ずつずらして配置し、それぞれのコイルに三相交流を流す。
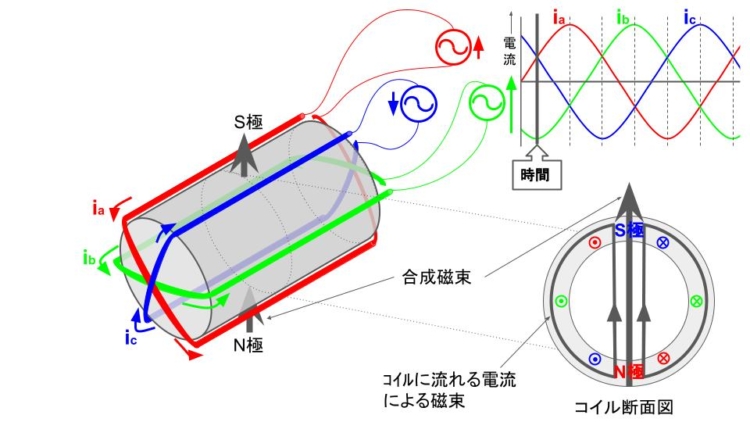
上図のように、三相交流電源を接続して電流を流したとすると、右ねじの法則に従ってコイルに流れる電流による磁束が発生する。これらの磁束は、図中にしめすような合成磁束となり、Ｎ極とＳ極が存在していると考えてよい。連続的に三相交流を流し続けることによりこの合成磁束は回転していき、磁石を回転させているのと同じ効果となる。（図をクリックすると合成磁束の回転変化が見れます）
このような合成磁束の回転速度を、同期回転速度ｎs[min-1]という。
三相誘導電動機の各種特性
三相誘導電動機の各種特性計算はこちら。
三相誘導電動機の種類
三相誘導電動機は、回転磁界を作る固定子及び回転する回転子からなる。回転子は、かご形回転子と巻線形回転子との２種類に分類される。
かご形誘導電動機
かご形誘導電動機では、回転子溝に導体（導体棒）を納めて、その両端が短絡環で接続される。
巻線形誘導電動機
巻線形誘導電動機では、回転子溝に巻線を納め、その巻線をスリップリングとブラシを介して外部回路に流すことができる。多くは、外部抵抗回路に接続し、二次電流を変化させて特性制御を行う。
巻線形誘導電動機では、外部の可変抵抗器で二次抵抗値を変化させ、大きな始動トルクと定格負荷時高効率の両方を実現することができる。始動電流を制限する効果もあり、回転速度が上昇するに従って抵抗値を減少させる。
巻線形誘導電動機では、トルクの比例推移により、二次抵抗の値を大きくすると、最大トルク（停動トルク）を発生する滑りが大きくなり、始動特性が良くなる。二次抵抗値を大きくとることで、低速起動時のトルク特性が改善するため、起重機クレーンなどの用途に用いられる。
三相巻線形誘導電動機は、回転磁界を作る固定子と回転する部分の巻線形回転子で構成される。
固定子は、電磁鋼板を円形又は扇形にスロットとともに打ち抜いて、必要な枚数積み重ねて積層鉄心を構成し、その内側に設けられたスロットに巻線を納め、結線して三相巻線とすることにより作られる。
一方、巻線形回転子は、積層鉄心を構成し、その外側に設けられたスロットに巻線を納め、結線して三相巻線とすることにより作られる。始動時には高い電圧にさらされることや、大きな電流が流れることがあるので、回転子の巻線には、耐熱性や絶縁性に優れた絶縁電線が用いられる。一般的に、小出力用では、ホルマール線やポリエステル線などの丸線が、大出力用では、ガラス巻線の平角銅線が用いられる。三相巻線は、軸上に絶縁して設けた3個のスリップリングに接続し、ブラシを通して外部(静止部)の端子に接続されている。この端子に可変抵抗器を接続することにより、始動特性を改善したり、速度制御をすることができる。
- 電験３種過去問【2022年(後期)機械 問3】（三相誘導電動機の構造）
- 電験３種過去問【2022年(前期)機械 問7】（各種電動機の性質）
- 電験３種過去問【2022年(前期)機械 問3】（三相巻線形誘導電動機の構造）
- 電験１種過去問【2016年機械制御 問1】（巻線形誘導電動機、各種運転条件での二次入力計算）
- 電験１種過去問【2012年機械制御 問1】（巻線形誘導電動機、単位法での計算、滑りの比例推移）
- 電験１種過去問【2011年機械制御 問1】（巻線形誘導電動機、同期ワットで表すトルク、二次励磁電源）
特殊かご形誘導機
かご形誘導機の始動特性の特徴として始動電流が大きい割に始動トルクが小さいことがあげられる。始動特性を改良するために二次周波数の変化に対する二次抵抗の変化を利用したのが特殊かご形誘導機である。
二重かご形誘導電動機
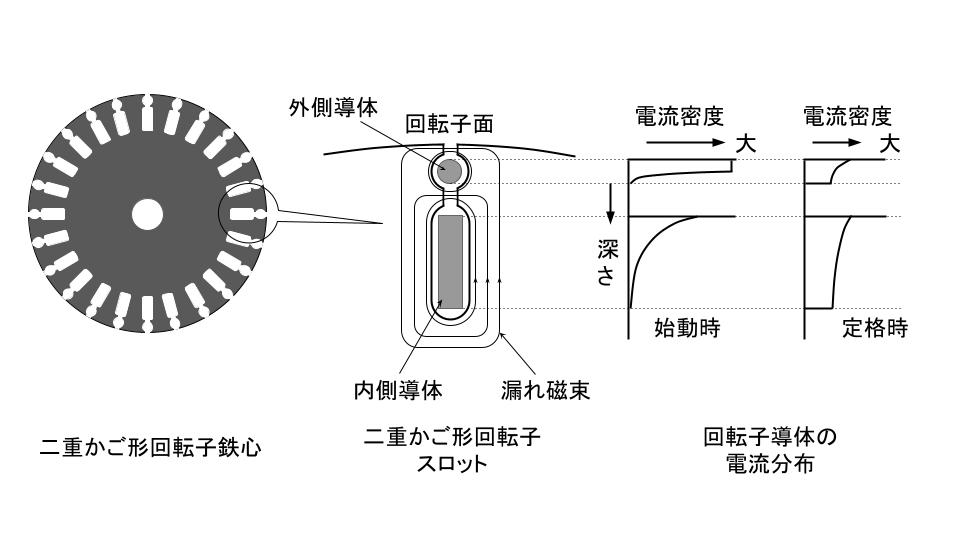
二重かご形誘導機の回転子は、二つのかご形導体を有している。回転子表面に近い外側導体は断面積が小さく、抵抗値が大きい。軸に近い内側導体は断面積が大きく、抵抗値が小さい。始動時の二次周波数が高い間は、内側導体が構成する二次回路の漏れインダクタンスが大きいため、二次回路を流れる電流の大部分は外側導体を流れる。そのため、二次抵抗の高い誘導機として始動され、大きな始動トルクを得ることができる。二次周波数の低下に伴い、二次電流の大部分は抵抗の低い内側導体に流れる。
このような二次抵抗の変化を利用し、大きな始動トルクと定格負荷時高効率の両方を実現することができる。
深みぞかご形誘導電動機
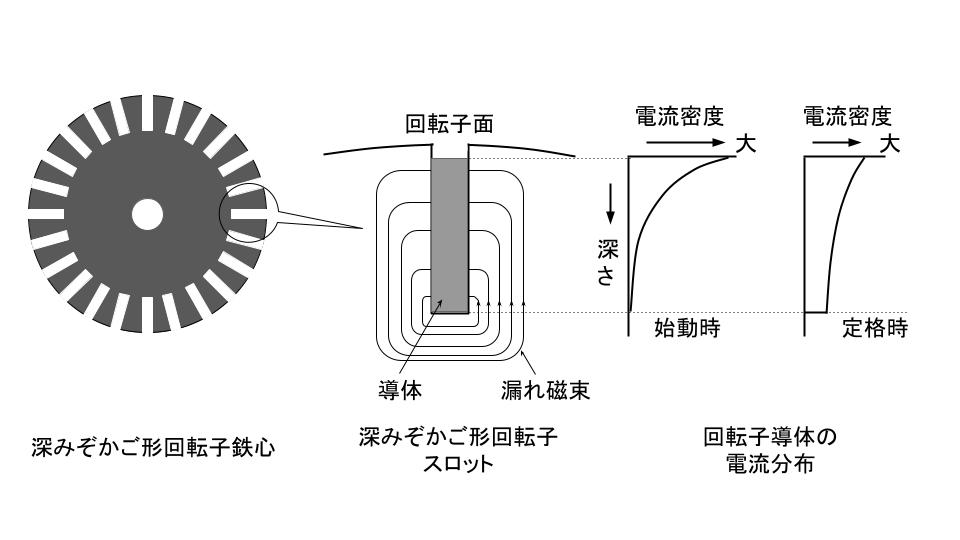
深みぞかご形誘導機の回転子には半径方向に長く、幅が狭い平たい二次導体を用いている。始動時の二次周波数が高い間は、二次電流は表皮効果により導体の回転子表面近くに集中し二次抵抗は高くなる。二次周波数の低下に伴い、二次電流が導体の軸に近い部分まで広がるので、二次抵抗は低くなる。
この抵抗値の変化を利用し、大きな始動トルクと定格負荷時高効率の両方を実現することができる。
単相誘導電動機
三相交流を三相巻線に流すと回転磁界が発生する。この磁界で運転される誘導電動機を三相誘導電動機という。一方、単相交流では交番磁界が発生する。この交番磁界は、正逆両方向の回転磁界が合成されたものと説明される。したがって、コンデンサ始動形単相誘導電動機では、コンデンサで位相を進めた電流を始動巻線に短時間流すことによって始動トルクの発生と回転方向の決定が行われる。
単相誘導電動機の単相巻線に発生する交番磁界は、互いに反対方向に同期速度で回転し、大きさが交番磁界の\(\frac{1}{2}\)である二つの回転磁界に分解できる。回転子が静止しているとき、これらの回転磁界は互いに逆方向のトルクを生じさせるので、始動トルクは零となる。しかし、どちらかの方向に少し回してやると回転子はその方向に加速し、同期速度に近い速度で定常運転に入る。
単相誘導電動機は、互いに反対方向に回転する二つの回転磁界が存在することから、回転子が機械的に直結され、回転磁界の回転方向が異なる二つの同じ二相誘導電動機と考え、その等価回路は図のように表すことができる。等価回路の A の部分は回転子の回転方向と同方向にトルクを発生する正相電動機、B の部分は回転方向と逆方向のトルクを発生する逆相電動機の等価回路である。正相電動機の滑りを s とするとき、逆相電動機の滑り sN は 2-s となる。
交流整流子モータ
交流整流子モータは、直流直巻電動機に類似した構造となっていて、加える電圧の極性を逆にしても、磁束と電機子電流の向きが共に逆になるので、トルクの向きは変わらない。つまり交流電源を加えても、回転の向きは変化しない。
交流整流子モータは、一般に始動トルクが大きく、回転速度が高速なので、電気ドリル、電気掃除機、小型ミキサなどのモータとして用いられている。なお、小容量のものでは、交流と直流の両方に使用できるものもあり、ユニバーサルモータと呼ばれる。
- 電験２種過去問【2021年機械 問3】（特殊かご形誘導機の原理）
- 電験３種過去問【2021年機械 問3】（各種誘導電動機の特徴）
- 電験３種過去問【2021年機械 問4】（各種誘導電動機の固定子と回転子）
- 電験３種過去問【2020年機械 問6】（交流整流子モータに関する知識）
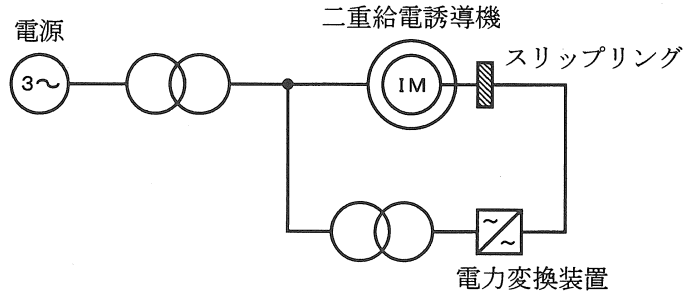
二重給電誘導電動機
図示されるように、二重給電誘導機は一次巻線が商用周波数の電源に接続され、二次巻線にはスリップリングを介して電力変換装置によって交流二次電流が供給される。電力変換装置は専用の変圧器を介して二重給電誘導機の一次側と同じ電源に接続される。回転速度の変化に応じて電力変換装置が常に滑り周波数をもつ交流二次電流を供給することで、二重給電誘導機は電源側との同期運転を行うことができる。
電力変換装置により二次電流の大きさと周波数を制御することによって、電力変換装置と二次巻線との間で双方向に交流電力を制御することが可能である。静止セルビウス方式と比較して同期速度以上での運転が可能なため、この方式は超同期セルビウス方式と呼ばれる。
電力変換装置としてはサイクロコンバータが一般的であるが、交流間接変換装置も適用される。電力分野への代表的な適用例として、可変速揚水発電システムやエネルギー変換効率向上を意図した可変速風力発電システムなどがある。
