パワーエレクトロニクスの学習帳

2021年3月7日2024年7月12日

スイッチング損失

ワーMOSFET、IGBT等のスイッチングデバイス（以下、スイッチと略す）のスイッチがオン状態の損失をオン損失と呼ぶ。オン状態のスイッチの端子間電圧は理想的にはゼロであるが、実際にはゼロではない。この電圧をオン電圧と呼び、この値が大きいスイッチのオン損失は大きい。一方、スイッチがオフ状態の損失をオフ損失と呼ぶ。オフ状態のスイッチを流れる電流は理想的にはゼロであるが実際にはゼロにならず、微小な漏れ電流が流れる。しかし漏れ電流は非常に小さく、オフ損失はオン損失に比べて十分に小さい。
　スイッチのターンオンとターンオフは瞬時に行われることが理想的である。しかし、実際の回路では、スイッチのターンオン・ターンオフ時に、スイッチの端子間電圧とスイッチを流れる電流がともにゼロではない期間が存在し、この期間に生じる損失はスイッチング損失と呼ばれる。単位時間あたりの損失は、スイッチのターンオンとターンオフの繰り返し周期が短いほど大きい。スイッチング損失を低減する方法の一つがソフトスイッチングであり、ターンオン時の端子間電圧 $v_{SW}$ と電流 $i_{SW}$ の波形は、例えば、図のようになり、 $v_{SW}$ がオン電圧になった後に $i_{SW}$ が上昇する。

電験２種過去問【2022年機械問4】（スイッチング損失）

IGBTとパワーMOSFET

パワー半導体スイッチングデバイスとしては近年、主にIGBTとパワーMOSFETが用いられている。両者を比較する。

　IGBTは電圧駆動形であり、ゲート・エミッタ間の電圧によってオン・オフを制御する。オンのゲート電圧が与えられればコレクタ・エミッタ間に電流が流れる。
　パワーMOSFET は電圧駆動形であり、ゲート・ソース間に正の電圧をかけることによりターンオンする。キャリア蓄積効果がないのでスイッチング速度が早く、スイッチング損失特性はIGBTに比べ優れている。
　パワーMOSFET はユニポーラデバイスであり、一般的にバイポーラ形の IGBT と比べてターンオン時間が短い一方、オン状態の抵抗が高く、流せる電流は小さい。
　IGBT はキャリアの蓄積作用のためターンオフ時にテイル電流が流れ、パワーMOSFET と比べてオフ時間が長くなる。
　パワーMOSFET ではシリコンのかわりに SiC を用いることで、高耐圧化と高耐熱化をしつつオン状態の抵抗を低くすることが可能になる。
IGBTはバイポーラトランジスタにパワーMOSFETの特徴を組み合わせることにより、スイッチング特性を改善している。

DC-DCコンバータ

降圧チョッパ

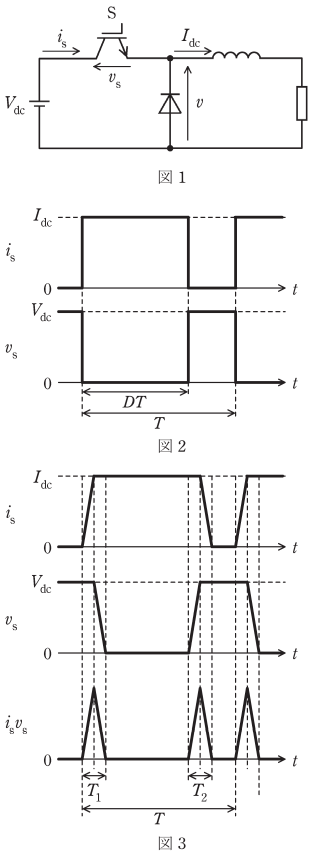
　図１は降圧チョッパの回路図である。この回路は直流電圧源Vdcを入力とし、出力電流Idcが半導体スイッチSとダイオードの間を転流する代表的な電力変換回路である。インダクタンスは十分に大きく、電流Idcにリプル成分は無いものとする。また、ダイオードの順電圧降下は無視する。
　図１の半導体スイッチSを理想的であると仮定した場合の電流isと電圧vsの波形を図２に示す。スイッチSは定数D(0≦D≦1)とスイッチング周期Tの積であるDTの期間に導通し、Dを通流率と呼ぶ。ダイオード電圧vの平均値Vは V= DVdcと表され、Dを変化させることによってダイオード電圧vの平均値を変えることができる。図２のどの時刻でも、理想的な半導体スイッチSの電流isと電圧vsの一方は零であることから、スイッチング損失は発生しない。
　半導体スイッチSのターンオン期間とターンオフ期間を考慮するため、図３に示す電流isと電圧vsのモデル波形を考えてみよう。ターンオフ期間とターンオン期間には、電流isと電圧vsが共に正である期間が存在する。図３において、ターンオフ期間ではvs=Vdcとなった後に電流isは減少し、ターンオン期間ではis=Idcとなった後に電圧vsは低下する。そのため、半導体スイッチSは損失を発生し、そのエネルギーは電流isと電圧vsの積isvsの面積によって求められる。電流isと電圧vsの変化は直線的と仮定すると、１回のターンオフ期間の損失Woff[J]はWoff＝12VdcIdcT2である。１回のターンオン期間の損失Won[J]も同様に求められる。したがって、半導体スイッチSにおけるスイッチング損失Ps[W]は Ps=Woff+WonTである。

電験３種過去問【2022年(前期)機械問10】（直流チョッパ回路の基本構成と降圧チョッパ）

電験２種過去問【2020年機械問2】（降圧チョッパのスイッチング損失）

昇降圧チョッパ

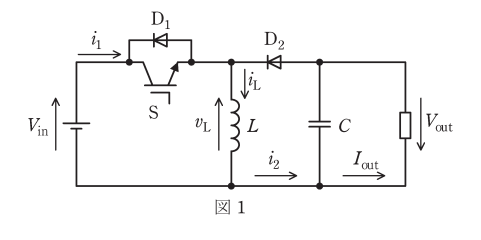
図１は昇降圧チョッパを示している。スイッチS、ダイオードD、リアクトルL、コンデンサCを用いて、図のような向きに定めた負荷抵抗Rの電圧 $V_{out}$ を制御するためのものである。これらの回路で、直流電源 $V_{in}$ の電圧は一定とする。また、回路の時定数は、スイッチSの動作周期に対して十分に大きいものとする。回路のスイッチSの通流率γとした場合

（１）Sがオンのときは、電源EからのエネルギーがLに蓄えられる。

（２）Sがオフのときは、Lに蓄えられたエネルギーが負荷抵抗RとコンデンサCに $D_{2}$ を通して放出される。

（３）出力電圧 $V_{out}$ の平均値は、γが0.5より大きいときは昇圧チョッパ、0.5より小さいときは降圧チョッパとして動作する。

（４）出力電圧 $V_{out}$ の平均値は、図の $V_{out}$ の向きを考慮すると正になる。

（５）Lの電圧v_Lの平均電圧は、Sのスイッチング一周期で0となる。

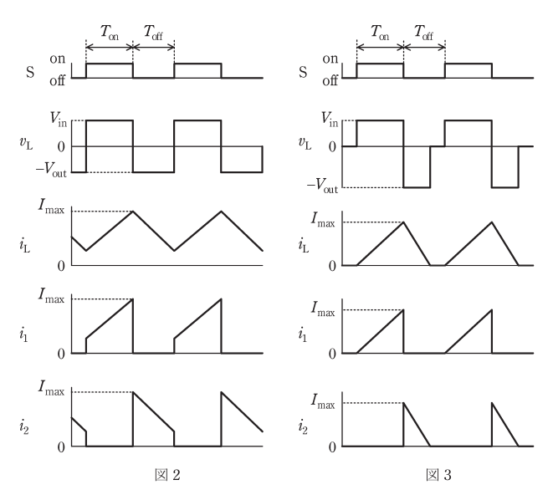
　平滑コンデンサCの静電容量は十分に大きく、出力電圧 $V_{out}$ 及び出力電流 $I_{out}$ のリプルは無視できるものとする。図２，３は、定常状態におけるインダクタの電圧 $v_{L}$ 及び電流 $i_{L}$ の波形であり、スイッチSがオンの期間を $T_{on}$ 、オフの期間を $T_{off}$ とする。
図２は出力電流 $I_{out}$ が大きく、インダクタ電流 $i_{L}$ が常に正の場合で、電流連続モードと呼び、このときの出力電圧が、 $V_{out}=\displaystyle\frac{T_{on}}{T_{off}}V_{in}$ となることは、よく知られている。ここで、デューティ比 $\displaystyle D=\frac{T_{on}}{T_{on}+T_{off}}$ を用いると、 $V_{out}=\displaystyle\frac{D}{1-D}V_{in}$ と表すこともできる。
一方、出力電流 $I_{out}$ を低減すると、図３のようにインダクタ電流 $i_{L}$ に零となる期間が現れる。図３の場合を電流断続モード（電流不連続モード）と呼ぶ。定常状態では、インダクタ電圧 $v_{L}$ の１周期の平均値は常に零でなければならない。電流連続モードと電流断続モードとスイッチSのゲート信号が同じであれば、 $V_{out}$ は電流断続モードの方が高くなる。

電験１種過去問【2020年機械制御問3】（DC-DC変換回路、波形作図、リプル計算）

単相半波整流回路

図１は単相半波ダイオード整流回路で、抵抗RとリアクトルLとを直列接続した負荷に電力を供給する。また図１に示した回路の電圧波形と電流波形を図２に示す。ただし、ダイオードDの電圧降下及びリアクトルLの抵抗は無視している。

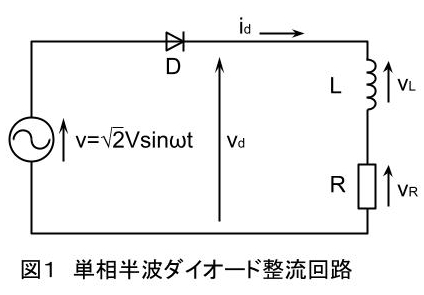
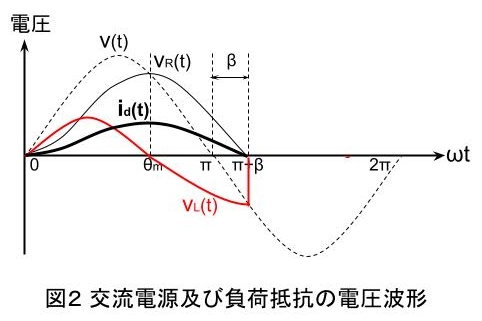
図１の電源電圧v(t)>0の期間においてダイオードＤは順方向バイアスとなり導通する。v(t)とv_R(t)が等しくなる電源電圧v(t)の位相をωt=θ_mとすると、出力電流i_d(t)が増加する電源電圧の位相ωtが0<ωt<θ_mの期間においては $vL(t)>0$ 、ωt=θ_m以降については $vL(t)<0$ となる。

出力電流i_d(t)は電源電圧v(t)が負となってもv(t)=0の点よりもωt=βに相当する時間だけ長く流れ続ける。これは、Ｌの磁気エネルギーが0となるωt=π+βで出力電流i_d(t)が0となる。出力電圧v_d(t)の平均値V_dは電源電圧v(t)を0～ $π+β$ の区間で積分して一周期である2πで除して計算でき、このときＬの電圧v_L(t)を同区間で積分すれば0となるので、V_dは抵抗Ｒの電圧v_R(t)の平均値V_Rに等しくなる。

電験３種過去問【2021年機械問16】（単相半波整流回路の動作）

単相全波整流回路

電験１種過去問【2010年機械制御問3】（単相全波整流回路、波形作図、動作説明）

単相ブリッジ整流回路

交流電源の電圧は正弦波で、電圧実効値を V 、制御遅れ角 α で運転していて、直流回路のインダクタンスは十分に大きく直流電流 I_d は一定とし、重なり角、回路の損失などは無視できるものとする。
直流出力電圧の平均値は V_d= $\frac{2\sqrt{2}}{π}$ cosα=0.90Vcosα [V]

電験１種過去問【2015年機械制御問3】（直交電力変換、単相整流回路、動作説明作図）

三相ブリッジ整流回路

　交流電源の電圧は三相対称正弦波で、線間電圧実効値を V 、相順は a→b→c 相とする。制御遅れ角 α で運転していて、直流回路のインダクタンスは十分に大きく直流電流 I_d は一定とし、重なり角、回路の損失などは無視できるものとする。

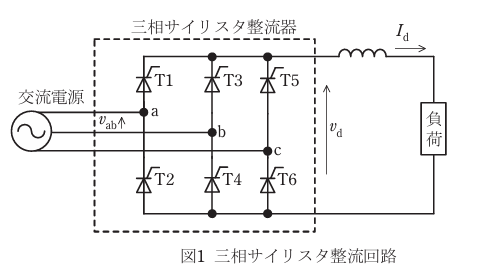
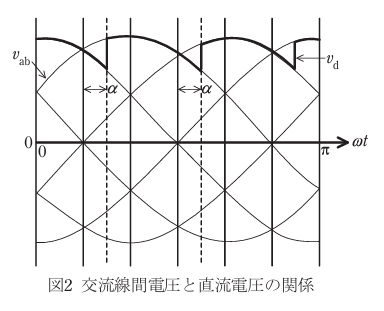
直流出力電圧の平均値は V_d= $\frac{3\sqrt{2}}{π}$ cosα=1.35Vcosα [V]
入力有効電力 P_a=1.35VI_dcosα [W]
入力皮相電力 S_a=1.35VI_d [VA]
入力無効電力 Q_a=1.35VI_dsinα [Var]
総合力率 λ= $\frac{P_a}{S_a}$

インバータ

単相インバータの特徴

　図３は電圧形インバータであり、直流電源 E の高周波インピーダンスが低いことが要求される。
　交流出力の調整は、 Q₁～Q₄ に与えるオンオフ信号の幅 $\displaystyle \frac{T}{2}$ を短くすることによって交流周波数を高くすることができる。又は、E の直流電圧を高くすることによって交流電圧を高くすることができる。
　図３に示されたスイッチングデバイスをパワートランジスタ、IGBT 又はパワーMOSFET に置換えてもインバータを実現できる。
　スイッチングデバイスに並列にダイオードが接続されているのは負荷のインダクタンスに蓄えられたエネルギーを直流電源に戻すためであり、さらにダイオードが導通することによって逆電圧によるスイッチング素子（トランジスタ）の破損を防止している。
　インダクタンスを含む負荷としては誘導電動機も駆動できる。運転中に負荷の力率が低くなると、電流がダイオードに流れる時間が長くなる。

電圧形インバータ

　電圧形インバータでは、スイッチングデバイス $Q_1$ と $Q_2$ に交互にオン信号とオフ信号を与えることにより、直流電源から交流電源を作り出す。

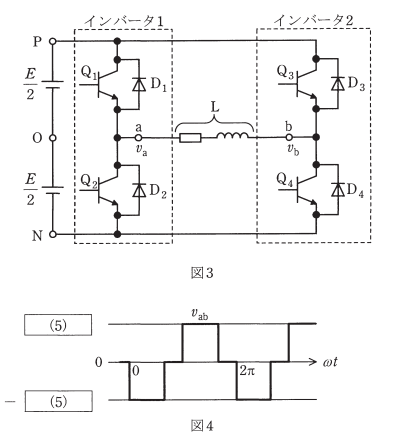
　図１には電圧形ハーフブリッジインバータを示す。負荷は誘導性負荷Lで、今 $Q_1$ がオンして負荷電流が $P-Q_1-L-O$ の経路で流れているとする。その後のある時刻で、 $Q_1$ をオフして $Q_2$ にオン信号を与えた。この直後に流れる電流の経路は $N-D_2-L-O$ となる。実際の電圧形インバータでは、 $Q_1$ にオフ信号を与えてから $Q_2$ にオン信号を与えるまでに所定の時間をとっている。この時間をデッドタイムといい、ターンオフの遅れなどによって短絡電流が流れるのを未然に防止する目的で設けている。電圧形インバータでは、直流電源とインバータからなる回路のインダクタンスを小さくしてあるもので、もし短絡すると大きな短絡電流が流れてしまう。
図１のインバータの出力電圧波形を図２に示す。この電圧 $v_a$ は、直流電源の中間電位点O端子からa端子を見たときの電圧である。図１のハーフブリッジインバータを２台使用したのが、図３の電圧形フルブリッジインバータである。このときの出力電圧 $v_{ab}$ は、 $v_{ab}=v_a-v_b$ と表せる。インバータ１とインバータ２が位相差120°で運転したときの出力電圧波形は図４となり、この電圧 $v_{ab}$ の波高値はEとなる。

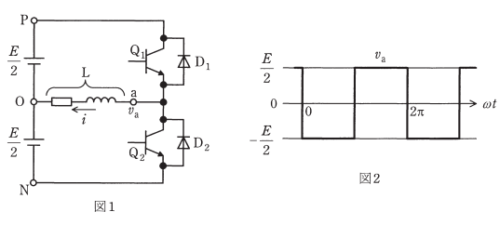
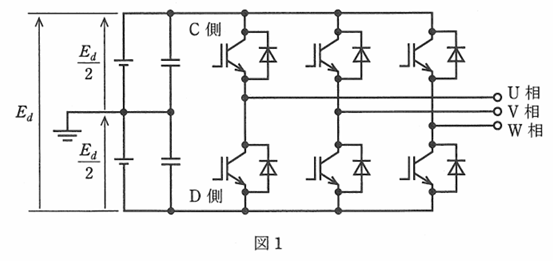
　スイッチング素子に対して並列に接続されるダイオードを還流ダイオードという。このダイオードの極性は直流電源に電流が逆流するような向きになっており、スイッチング直後の逆電流をダイオード側に流すことにより、逆電流によるスイッチング素子の破損を防止している。

電験１種過去問【2021年機械制御問2】（単相インバータ、フェーザ図、電力計算）

三相インバータ

三角波搬送波の周波数と特徴

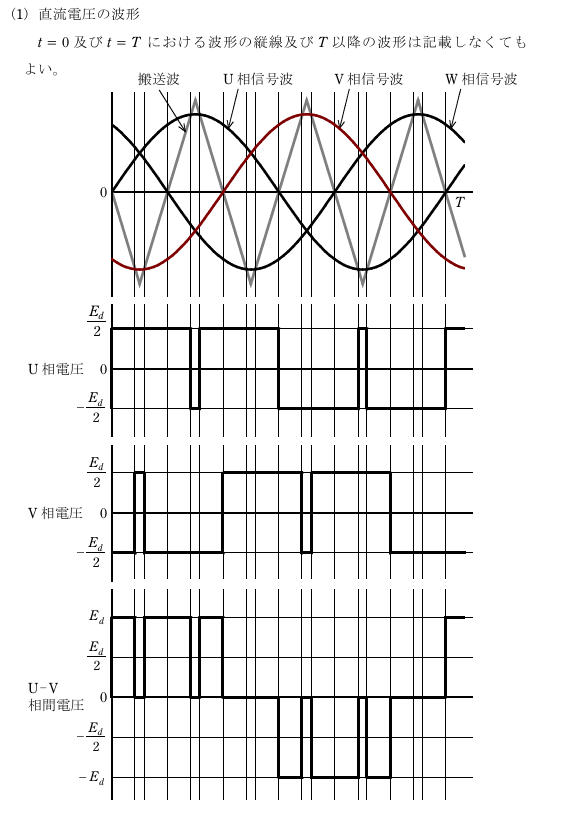
搬送波の周波数を信号波の周波数の3の奇数倍とする理由
●3の倍数とする理由
・上図のように３の倍数とすることで、三相間で電圧波形を同じにできる。
・相間で3の倍数次の高調波を相殺し抑制できる。
●奇数倍とする理由
・偶数次高調波の発生を抑制できる。
・正と負の波形を同じにできる。
搬送波の周波数を高くしたときのメリット，デメリット
●メリット
・電流波形を正弦波に近づけられる。
・フィルタを小形にできる。
●デメリット
・損失が増加する。
・騒音が大きくなりやすい。

回生制御

　負荷の状態によっては、誘導電動機の入力電力が負になるときがある。このような時は回生制御を行うことにより、負の電力を処理する必要がある。
　ダイオード整流器を使用するのであれば、直流回路に電力を消費する抵抗とその電流を制御するスイッチを設け、直流電圧が過大にならないようスイッチをオンオフ制御する発電運転を行う。あるいは、直流回路からチョッパを介して二次電池を接続し、直流電圧が過大にならないように電池の充放電制御を行う。
　あるいは、ダイオード整流器を回生用 PWM コンバータに置き換え、直流電圧が一定になるように PWM コンバータで電圧制御を行う。

電験１種過去問【2019年機械制御問3】（負荷トルク特性、慣性モーメント、入力電力の正負と負電力処理法）

単相交流電力調整装置

電験２種過去問【2019年機械問3】（単相交流電力調整装置の動作）

電験学習帳学習, 機械, パワエレ

Posted by ちゅん

ディスカッション

コメント一覧

まだ、コメントがありません