照明の学習帳
照明
可視放射光
放射とは、電磁波あるいは粒子の形によって伝搬するエネルギーのことである。電磁波の波長範囲は、\(10^{-16}~10^8\)mであり、その波長によって宇宙線、ガンマ線、X線、紫外放射、可視放射(光)、赤外放射、電波などに区分され、それぞれ特有の性質を持っている。このうち人の目に入って、明るさの感覚を生じさせる380~780mmの波長範囲を可視放射(光)という。
単位時間にある面を通過する放射エネルギーの量を放射束という。単位はワット[W]又はジュール毎秒[J/s]であり、物理量である。
放射束に明所視下における人の目の感度(分光視感効率)を乗じた量\(\Phi\)を光束といい、単位はルーメン[lm]である。これは、物理量に人の目の感度を乗じた量であることから、心理物理量と呼ばれる。また、この\(\Phi\)は、ある放射体からの分光放射束を\(\Phi_e(\lambda)\)[W/nm]、標準分光視感効率を\(V(\lambda)\)とすれば、次式より求まる。
\(\Phi=K_m\int_{\lambda_1}^{\lambda_2}V(\lambda)\Phi_e(\lambda)d\lambda\)
ここで、\(\lambda\)は波長[nm]、\(\lambda_1から\lambda_2\)までは可視放射(光)の波長範囲、\(K_m\)は最大視感効果度であり、その値は約555nmにおいて約683lm/Wである。
ルミネセンス
ルミネセンスとは、物質を構成する原子、分子、イオン、電子などが、外部からのエネルギーを吸収して、励起、イオン化又は加速された後、そのエネルギーを放出するときに発光する現象をいう。
放電発光は、放電により原子や分子が電離又は励起され、電子状態の遷移に伴って発光する現象である。HIDランプなどがこれを利用している。
フォトルミネセンスは、物質がX線、紫外放射、可視放射、赤外放射などを受けたときにそのエネルギーを吸収し、通常は吸収した波長よりも長波長の放射エネルギーを放出して発光する現象である。蛍光ランプ及び白色LEDの蛍光体ではこの現象を利用している。
エレクトロルミネセンス(EL)は、物質に電界を印加することによって発光する現象で、注入形ELと真性ELとに区別される。注入形ELは、電界を印加することによって電子及び正孔を注入し、その再結合過程で発光する現象である。LED、有機ELなどがこれを利用している。真性ELは、蛍光体を分散させた薄い誘電体をサンドイッチ状に挟んだ電極両端に電圧を印加することによって発光する現象である。
光の基本量
光束
光源の放射束のうち人の目に光として感じるエネルギーを光束といい単位にはルーメン([lm])を用いる。
光度
光源の各方向に出ている光の強さを示すものが光度である。光度\(I\) カンデラ([cd])は、立体角ω [sr] から出る光束を F [lm]とすると\(\displaystyle I=\frac{F}{\omega}\)で示される。
光源から出てある方向の立体角Δω [sr] に放射される光束をΔF [lm] とするとき、光度Iは
\(\displaystyle I=\frac{ΔF}{Δω}\text{[cd]}\)
全球の立体角ω=4π[sr](ステラジアン)である。
輝度
光源の発光面及び反射面の輝きの程度を示すのが輝度であり、単位には[cd/m²]を用いる。
輝度L[cd/m2]は、面光源を観測点から見た時、観測点を通過する単位面積S(観測者から見て垂直な平面上に投影した正射影面積)当たりの光度Iで定義される。輝度は観測者が対象を見たときの明るさを表す指標であり、ディスプレイなどの面光源の明るさを表す指標として用いられる。
\(\displaystyle L=\frac{I}{S}\)[cd/m2]
照度
照度は、光を受ける面の明るさの程度を示し、1ルクス([lx])とは被照射面積 1 m² に光束1[lm]が入射しているときの、その面の照度である。
照度の定義
面積ΔA[m2]に放射される全光束をΔF[lm]とすれば、照度E[lx]は
\(\displaystyle E=\frac{ΔF}{ΔS}\text{[lx]}\)
点光源照度からの距離の逆2乗の法則
光度の定義\(\displaystyle I=\frac{ΔF}{Δω}\text{[cd]}\)より、
光度I[cd]の点光源からは
\(\displaystyle F=4\pi I\text{[lm]}\)
の光束が全空間(ω=4π)に均等に発散している。
下図のように、点光源を中心とした半径l[m]の球を考えると、点光源からのすべての光束は球表面に到達する。このため球の表面の照度E[lx]は
\(\displaystyle E=\frac{F}{S}=\frac{4\pi I}{4\pi l^2}=\frac{I}{l^2}\text{[lx]}\)
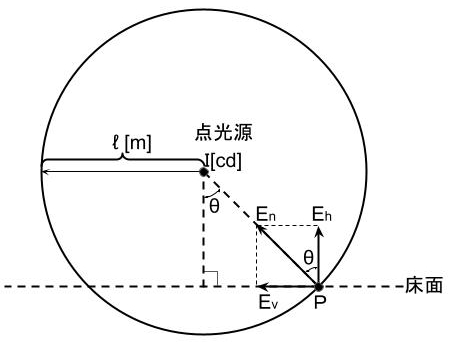
ここで表される照度Eはその点から球の中心(点光源)へ向かう方向の照度で法線照度\(\displaystyle E_n\)と呼ぶ。
法線照度 \(\displaystyle E_n=\frac{I}{l^2}\text{[lx]}\)
水平面照度 \(\displaystyle E_h=\frac{I}{l^2}cos\theta\text{[lx]}\)
鉛直面照度 \(\displaystyle E_v=\frac{I}{l^2}sin\theta\text{[lx]}\)
光束発散度
物体の単位面積から発散する光束の大きさを光束発散度M[lm/m²]といい、ある面から発散する光束を F 、その面積を A [m²] とすると\(\displaystyle M=\frac{F}{A}\)で示される。
光源から発散される光束\(\displaystyle F_0\)[lm]について、光源の全表面上\(\displaystyle A_0\)[m2]から拡散する密度で表したもの。
\(\displaystyle M=\frac{F_0}{A_0}\text{[lx]}\)
相互反射
下図にように、光源の光束をF[lm]、グローブの反射率をρ、透過率をτとする。
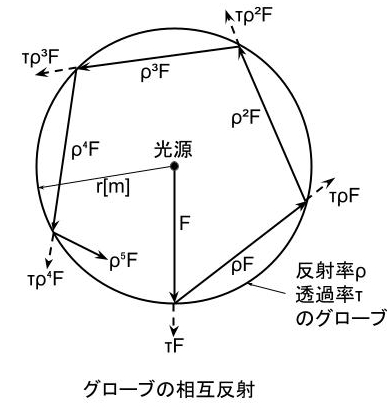
このとき、グローブ内面の反射光束\(\displaystyle F_0\)[lm]は
\(\displaystyle F_0=F+ρF+ρ^2F+ρ^3F+…\)
\(\displaystyle =F+ρF(1+ρ+ρ^2+ρ^3+…) \) ∵等比数列\(\displaystyle \sum_{i=0}^\infty x_i=\frac{1}{1-x} (|x|<1)\)
\(\displaystyle =F+ρF\frac{1}{1-ρ}=\frac{F-ρF+ρF}{1-ρ}\)
\(\displaystyle =\frac{F}{1-ρ}\text{[lm]}\)
グローブ内面の照度E[lx]は
\(\displaystyle E=\frac{F_0}{4\pi r^2}=\frac{F}{(1-ρ)4\pi r^2}\)
\(\displaystyle =\frac{F}{4\pi r^2}+\frac{ρF}{(1-ρ)4\pi r^2}\text{[lm]}\)
上式の\(\displaystyle \frac{F}{4\pi r^2}\text{[lm]}\)は直射照度、\(\displaystyle \frac{ρF}{(1-ρ)4\pi r^2}\text{[lm]}\)は拡散照度を表す。
透過光束\(\displaystyle F_τ\)[lm]は
\(\displaystyle F_τ=τF+τρF+τρ^2F+τρ^3F+…\)
\(\displaystyle =τF(1+ρ+ρ^2+ρ^3+…) \)
\(\displaystyle =τF\frac{1}{1-ρ}\)
\(\displaystyle =τF_0\text{[lm]}\)
グローブの効率ηは
\(\displaystyle η=\frac{F_τ}{F}\times100=\frac{τ}{1-ρ}\times100\text{[lm]}\)
平均照度
室の天井面に複数の照明器具(同一種類のもの)を規則的に配置して、室内全体の照明を行い、所望の照度を得ることを考える。光束法を用いて、室の作業面の平均照度(設計値)E [lx]は次式によって求めることができる。ただし、床面積A[m2](間口[m]×奥行[m])、光源1灯の定格光束\(\Phi\)[lm]、光源数N[個]、照明率U、保守率Mとする。
\(\displaystyle E=\frac{\Phi NUM}{A}\)[Lx]
照明率Uとは、光源から出た光のうち、作業面に到達する光(床・壁・天井・反射板等での相互反射などで光は減衰する)どれほどかを示す割合。照明器具の配光、器具効率、室の寸法(XとY)、作業面からランプまでの高さ、室内面(天井、壁、床)の反射率によって決まる係数。
保守率Mとは、照明設計の段階で、光源自身の光束減退や照明器具の汚れ等による照度低下を補うために、照度計算の中に補正係数を設けたもの。この値に応じて施設に必要な照度レベルより高い照度レベルで設計を行うもの。保守率(M)は、新設時に見込む照度(初期照度Ei)とその施設で確保すべき照度(照明器具の清掃および古い光源の交換を行う直前の照度Et)の比(M=Et/Ei)で定義される。
新設時の平均照度に対する、ある一定期間使用した後の平均照度の比。ランプは使用しているうちに光束がしだいに減少し、照明器具は汚れによって器具効率が低下する。このために、設計の際に光束にあらかじめ余裕をもたせておくための係数。

ディスカッション
コメント一覧
まだ、コメントがありません