電験３種過去問【2022年(下期)機械 問17】
【照明】均等放射点光源の光度と照度《計算問題》
どの方向にも光度が等しい均等放射の点光源がある。この点光源の全光束は 3000 lm である。この点光源を図のように配置した。水平面から点光源までの高さは 2 m であり、点光源の直下の点 A と B との距離は 1.5 m である。次の(a)及び(b)の問に答えよ。
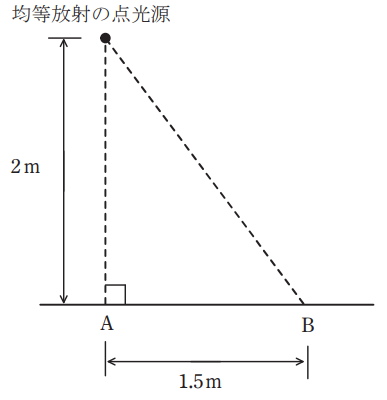
(a) この点光源の平均光度[cd]として、最も近いものを次の（１）～（５）のうちから一つ選べ。
(1) 191
(2) 239
(3) 318
(4) 477
(5) 955
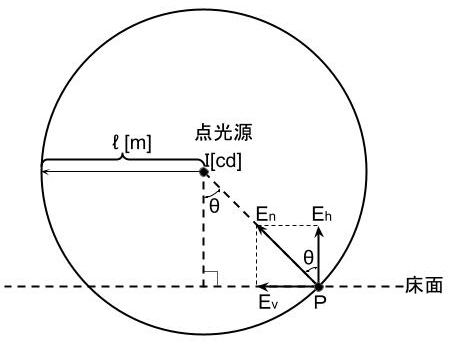
(b) 水平面 B 点における水平面照度の値 [lx] として、最も近い値を次の（１）～（５）のうちから一つ選べ。
(1) 10
(2) 24
(3) 31
(4) 61
(5) 122
解答
（a）:（2）が正しい。
（b）:（3）が正しい。
解説
(a) 光源の平均光度[cd]は、以下の光度の定義より
光源から出てある方向の立体角Δω[sr]に放射される光束をΔF[lm]とするとき
光度Iは
\(\displaystyle I=\frac{ΔF}{Δω}\text{[cd]}\)
全球の立体角ω＝4π[sr](ステラジアン)である。
\(\displaystyle I=\frac{ΔF}{Δω}\text{[cd]}\)
\(\displaystyle =\frac{3000}{4\pi}=238.7\text{[cd]}\)
(b) 水平面B点の水平面照度[lx]は、以下の照度の式より
均等放射の点光源 I [cd] から l [m] 離れた点の水平面照度 Eh [lx]は、
水平面照度 \(\displaystyle E_h=\frac{I}{l^2}cos\theta\text{[lx]}\)
\(\displaystyle E_h=\frac{I}{l^2}cos\theta\text{[lx]}\)
\(\displaystyle =\frac{238.7}{(\sqrt{2^2+1.5^2})^2}\times cos\theta\text{[lx]}\)
\(\displaystyle =38.192cos\theta\text{[lx]}\)
ここで、
\(\displaystyle cos\theta=\frac{2}{\sqrt{2^2+1.5^2}}=0.8\)
\(\displaystyle E_h=38.192\times 0.8 =30.6\text{[lx]}\)