電験２種過去問【2020年理論 問3】

解答

解説

　テブナンの定理を用いて解く。

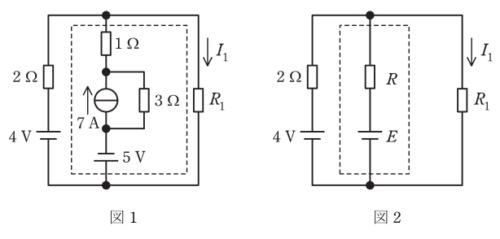
　図１の破線で囲まれた部分を切り離し、図２の破線部分に示す抵抗Ｒと電圧源Ｅに等価変換する。

電流源を開放除去、電圧源を短絡除去したときの抵抗値Ｒ＝\(\fbox{(ﾖ)4}\)Ω、

電流源7Aにより、3Ωの抵抗に係る電圧は21Vとなる。

したがってＥ＝21-5=\(\fbox{(ﾙ)16}\)Ｖとなる。

　図２から、抵抗\(R_1\)に流れる電流\(I_1\)を重ね合わせの理を用いて求める。

等価電源Eによる回路を考えるため、4V電源を短絡除去すると、合成抵抗\(R_E\)は

\(\displaystyle R_E=R+\frac{2R_1}{2+R_1}\)

\(\displaystyle =4+\frac{2R_1}{2+R_1}\)

\(\displaystyle =\frac{8+6R_1}{2+R_1}\)[Ω]

4V電源除去時の抵抗Rに流れる電流\(I_{ER}\)は

\(\displaystyle I_{ER}=\frac{E}{R_E}\)

\(\displaystyle =\frac{16}{\frac{8+6R_1}{2+R_1}}\)

\(\displaystyle =16\times\frac{2+R_1}{2(4+3R_1)}\)

\(\displaystyle =8\times\frac{2+R_1}{4+3R_1}\)

電流の分流則より、4V電源除去時の\(I_1\)部に流れる電流を\(I_{E1}\)とすると

\(\displaystyle I_{E1}=I_{ER}\times\frac{2}{2+R_1}\)

\(\displaystyle =\frac{16}{4+3R_1}\)[A]

同様にして、直流電源4Vによる回路を考えるため、等価電源Eを短絡除去し

等価電源E除去時の\(I_1\)部に流れる電流を\(I_{41}\)として計算すると

\(\displaystyle I_{41}=\frac{8}{4+3R_1}\)[A]

上記2つの回路を合成すると、抵抗\(R_1\)に流れる電流\(I_1\)は

\(\displaystyle I_{1}=I_{E1}+I_{41}\)

\(\displaystyle I_{1}=\frac{16}{4+3R_1}+\frac{8}{4+3R_1}\)

\(\displaystyle I_{1}=\frac{24}{4+3R_1}\)[Ａ]

となる。また、\(R_1\)で消費される電力Ｐは\(P=I_1^2R_1\)で求められる。

\(\displaystyle P=\left(\frac{24}{4+3R_1}\right)^2 R_1\)

\(\displaystyle =\frac{24^2R_1}{9R_1^2+16+24R_1}\)

\(\displaystyle =\frac{24^2}{9R_1+\frac{16}{R_1}+24}\)

上式の\(\displaystyle 9R_1+\frac{16}{R_1}\)の部分が最小であればPは最大となる。

相加相乗平均の不等式を用いると

\(\displaystyle 9R_1=\frac{16}{R_1}\)であるとき、\(\displaystyle 9R_1+\frac{16}{R_1}\)は最小となるので

\(\displaystyle 9R_1^2=16\)

\(\displaystyle R_1=\frac{4}{3}\)

したがって、\(\displaystyle R_1=\frac{4}{3}\)Ωのときに電力Ｐは最大となり、このとき

\(\displaystyle P=\left(\frac{24}{4+3R_1}\right)^2 R_1\)

\(\displaystyle =\left(\frac{24}{4+3\frac{4}{3}}\right)^2\frac{4}{3}\)

\(\displaystyle =12\)

Ｐ＝\(\fbox{(ｦ)12.0}\)Wとなる。 

※相加相乗平均については電験頻出の最小値を求めるパターンで解説しています。

<<前問　　次問>>

電験３種の過去問一覧

　電験３種の過去問を２００９年以降分からまとめています。 管理人の電験受験学習進捗に合わせて、順 ...

 https://archivelog.net/denken3-kakomon/

 

【まとめ】電験記事一覧

電験に関連する情報をまとめて掲載していきます。主に管理人学習用の備忘録です。過去問を中心に学習し ...

 https://archivelog.net/denken/