電験３種過去問【2021年理論 問18】

解答

（a）：（４）
（b）：（４）

解説

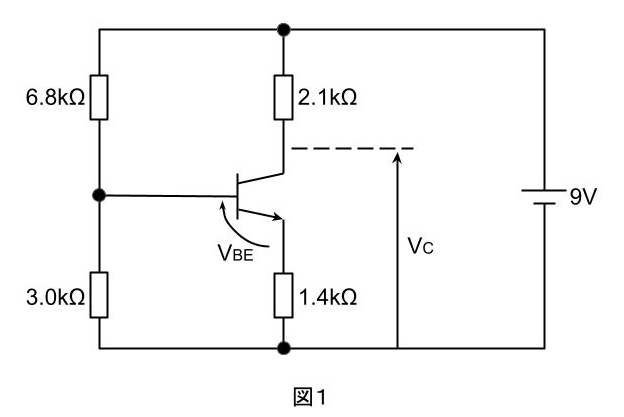
（a）3.0kΩの抵抗にかかる電圧V_B[V]は、6.8kΩと3.0kΩの抵抗に抵抗値に比例して分圧するので

\(\displaystyle V_B=9V\times\frac{3.0kΩ}{3.0kΩ+6.8kΩ}=2.76\text{[V]}\)

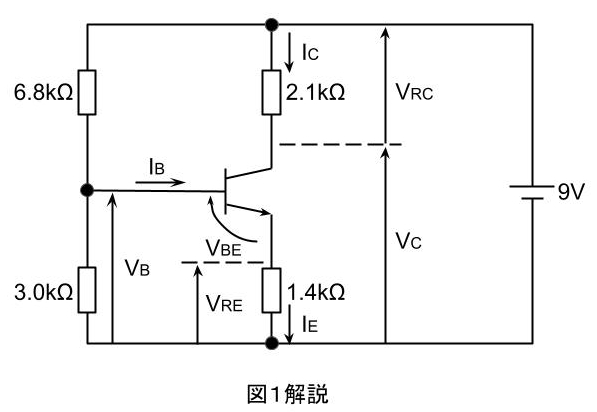
1.4kΩの抵抗にかかる電圧V_RE[V]は

\(\displaystyle V_{RE}=V_B-V_{BE}=2.76-0.6=2.16\text{[V]}\)

1.4kΩの抵抗に流れる電流I_E[A]は

\(\displaystyle I_E=\frac{V_{RE}}{1.4\times10^3}=1.54\times10^{-3}\text{[A]}\)

電流I_E[A]と、ベース電流I_B[A]及びコレクタ電流I_C[A]には次の関係がある。

\(\displaystyle I_E=I_B+I_C\)

ここで、\(\displaystyle I_C=h_{FE}I_B\)であるが、\(\displaystyle h_{FE}=100\)であるので

\(\displaystyle I_B≪I_C\)として、

\(\displaystyle I_E=I_B+I_C≒I_C\)

2.1kΩの抵抗にかかる電圧V_RC[V]は、同抵抗に流れる電流I_C[A]が、電流I_E[A]と等しいと考えられるので、

\(\displaystyle V_{RC}=I_C \times2.1\times10^3\)

\(\displaystyle =I_E \times2.1\times10^3\)

\(\displaystyle =1.54\times10^{-3}\times2.1\times10^3\)

\(\displaystyle =3.23\text{[V]}\)

求めるV_C[V]は、

\(\displaystyle V_C=9-V_{RC}=9-3.23=5.77\text{[V]}\)

 

（b）LC発振器の一般形における、発振振条件は、以下となる。

\(\displaystyle h_{fe}=\frac{Z_2}{Z_3}\)

\(\displaystyle \dot{Z_1}+\dot{Z_2}+\dot{Z_3}=0\)

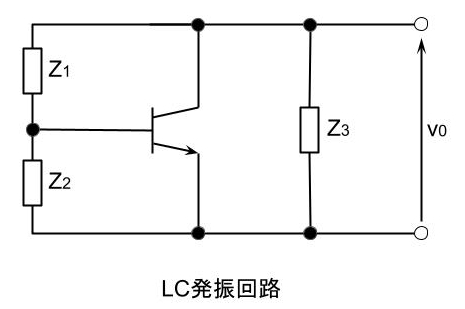
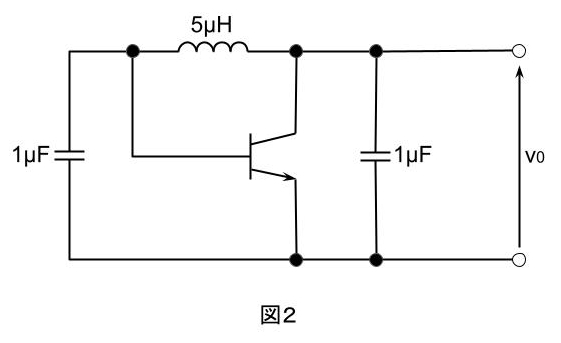
問題の回路は、コルピッツ発振回路であり、共振周波数fは

\(\displaystyle ωL_1-\frac{1}{ωC_2}-\frac{1}{ωC_3}=0\)

\(\displaystyle ωL_1-\frac{C_3}{ωC_2C_3}-\frac{C_2}{ωC_2C_3}=0\)

\(\displaystyle ωL_1-\frac{C_2+C_3}{ωC_2C_3}=0\)

\(\displaystyle ωL_1=\frac{C_2+C_3}{ωC_2C_3}\)

\(\displaystyle ω^2=\frac{C_2+C_3}{L_1C_2C_3}\)

\(\displaystyle (2\pi f)^2=\frac{C_2+C_3}{L_1C_2C_3}\)

\(\displaystyle f=\frac{1}{2\pi}\sqrt{\frac{C_2+C_3}{L_1C_2C_3}}\)

したがって、数値を当てはめると

\(\displaystyle f=\frac{1}{2\pi}\sqrt{\frac{2\times10^{-6}}{5\times10^{-18}}}\)

\(\displaystyle f=\frac{1}{2\pi}\sqrt{0.4\times10^{12}}\)

\(\displaystyle f=100\times10^{3}\text{[Hz]}\)