電験３種過去問【2021年電力 問16】

解答

（a）:（４）
（b）:（２）

解説

（a）電線の導体温度が35℃のとき、電線の支持点間の実長の値[m]を求める。

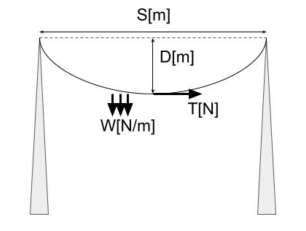
電線の実長L[m]は次式で求められる。ここで、電線の径間S[m]、電線のたるみD[m]。

$\displaystyle L=S+\frac{8D^2}{3S}$

$\displaystyle =150+\frac{8\times3.5^2}{3\times150}$

$\displaystyle =150.22$[m]

電線の実長L[m]のとき、温度変化による電線長L’[m]は、１[℃]あたりの線膨張係数をα、温度差をt[℃]とすると

$\displaystyle L’=L(1+αt)$

$\displaystyle =150.22(1+0.000 018\times45)$

$\displaystyle =150.34$[m]

 

（b）(a)と同じ条件のとき、電線の支持点間の最低点における水平張力の値[N]を求める。

電線の実長L[m]は次式で求められる。ここで、電線の径間S[m]、電線のたるみD[m]。

$\displaystyle L=S+\frac{8D^2}{3S}$

上式より、電線のたるみD[ｍ]は

$\displaystyle D^2=\frac{3S(L-S)}{8}$

$\displaystyle D^2=\frac{3\times150(150.34-150)}{8}=19.125$

$\displaystyle D=4.373$[m]

電線のたるみD[m]は次式で求められる。ここで、電線の径間S[m]、電線の水平張力T[N]、電線1ｍあたりの自重W[N/m]。

$\displaystyle D=\frac{WS^2}{8T}$

上式より水平張力T[N]は

$\displaystyle T=\frac{WS^2}{8D}$

$\displaystyle =\frac{20\times 150^2}{8\times4.373}$

$\displaystyle =12863$[N]