電験３種過去問【2021年電力 問17】

解答

（a）:（２）
（b）:（３）

解説

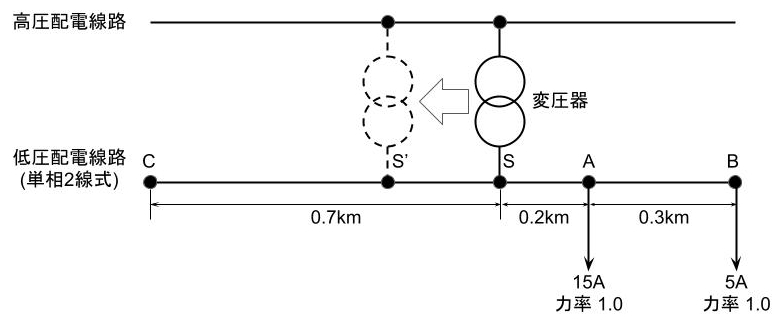
（a）B点におけるS点に対する電圧降下率の値[％]を求める。

S-A間の１線の抵抗値\(\displaystyle R_{SA}=0.3\times0.2=0.06\)[Ω]

S-A間の１線のリアクタンス値\(\displaystyle X_{SA}=0.4\times0.2=0.08\)[Ω]

S-A間の１線の電圧降下等価抵抗\(\displaystyle S_{SA}=R_{SA}cos \theta+ X_{SA}sin \theta\)[Ω]

題意より、力率\(\displaystyle cos\theta=1.0\)、\(\displaystyle sin\theta=0\)であるので、

\(\displaystyle S_{SA}=0.06\times 1+0.08\times 0=0.06\)[Ω]

S-A間に流れる電流は15A+5A＝20Aである。

S-A間の１線の電圧降下は１線の電圧降下等価抵抗\(\displaystyle S_{SA}=0.06\)[Ω]に流れる電圧降下であり、単相の場合、S-A間電圧降下\(\displaystyle V_{SA}\)は１線の電圧降下の２倍であるので、

\(\displaystyle V_{SA}=2\times 0.06\times20=2.4\)[V]

 

同様に、A-B間の電圧降下等価抵抗\(\displaystyle S_{AB}\)を求める。

A-B間の１線の抵抗値\(\displaystyle R_{AB}=0.3\times0.3=0.09\)[Ω]

A-B間の１線のリアクタンス値\(\displaystyle X_{AB}=0.4\times0.3=0.12\)[Ω]

A-B間の１線の電圧降下等価抵抗\(\displaystyle S_{AB}=R_{AB}cos \theta+ X_{AB}sin \theta\)[Ω]

力率\(\displaystyle cos\theta=1.0\)であるので、

\(\displaystyle S_{AB}=0.09\times 1+0.12\times 0=0.09\)[Ω]

A-B間に流れる電流は5Aである。

A-B間の１線の電圧降下は１線の電圧降下等価抵抗\(\displaystyle S_{SA}=0.09\)[Ω]に流れる電圧降下であり、単相の場合、S-A間電圧降下\(\displaystyle V_{AB}\)は往路・復路があり、１線の電圧降下の２倍であるので、

\(\displaystyle V_{AB}=2\times 0.09\times5=0.9\)[V]

電圧降下率εは、受電端電圧を基準とすると

\(\displaystyle ε=\frac{(2.4+0.9)}{107-(2.4+0.9)}\times 100=3.18\)[%]

 

（b）C点に電流20A、力率0.8（遅れ）の負荷が新設されるとき、変圧器の接続点をS点からS’点に変更し、B点及びC点における線間電圧の値が等しくなるときのS点からS’点への移動距離の値Ｌ[km]を求める。

前問(a)より、

S’-A間の電圧降下\(\displaystyle V_{S’A}\)は移動距離Lを考慮すると

\(\displaystyle V_{S’A}=2\times 0.3\times (0.2+L)\times20\)[V]

A-B間の電圧降下\(\displaystyle V_{AB}\)は移動距離Lに影響しないため

\(\displaystyle V_{AB}=2\times 0.09\times5=0.9\)[V]

S’-B間電圧降下\(\displaystyle V_{S’B}=V_{S’A}+V_{AB}=0.9+12\times (0.2+L)\)[V]

 

S’-C間の１線の抵抗値\(\displaystyle R_{S’C}=0.3\times (0.7-L)\)[Ω]

S’-C間の１線のリアクタンス値\(\displaystyle X_{S’C}=0.4\times (0.7-L)\)[Ω]

S’-C間の１線の電圧降下等価抵抗\(\displaystyle S_{S’C}=R_{S’C}cos \theta+ X_{S’C}sin \theta\)[Ω]

題意より、C点の力率\(\displaystyle cos\theta=0.8\)、\(\displaystyle sin\theta=0.6\)であるので、

S’-C間の１線の電圧降下等価抵抗\(\displaystyle S_{S’C}=0.24\times (0.7-L)+0.24\times (0.7-L)=0.48\times (0.7-L)\)[Ω]

S’-C間に流れる電流は20Aである。

S’-C間の１線の電圧降下は１線の電圧降下等価抵抗\(\displaystyle S_{S’C}=0.48\times (0.7-L)\)[Ω]に流れる電圧降下であり、単相の場合、S’-C間電圧降下\(\displaystyle V_{S’C}\)は１線の電圧降下の２倍であるので、

\(\displaystyle V_{S’C}=2\times 0.48\times (0.7-L)\times20=19.2\times (0.7-L)\)[V]

 

S’-B間電圧降下\(\displaystyle V_{S’B}\)とS’-C間電圧降下\(\displaystyle V_{S’C}\)が等しくなる条件は、

\(\displaystyle V_{S’B}=V_{S’C}\)

∴\(\displaystyle 0.9+12\times (0.2+L)=19.2\times (0.7-L)\)

∴\(\displaystyle 0.9+2.4+12L=13.44-19.2L\)

∴\(\displaystyle 31.2L=10.14\)

∴\(\displaystyle L=0.325\)[km]