電験3種過去問【2020年電力 問17】
【配電】配電線路の電圧降下と電流《計算問題》
図のような系統構成の三相3線式配電線路があり、開閉器Sは開いた状態にある。各配電線のB点、C点、D点には図のとおり負荷が接続されており、各点の負荷電流はB点40A、C点30A、D点60A一定とし、各負荷の力率は100%とする。
各区間のこう長はA-B間1.5km、B-S(開閉器)間1.0km、S(開閉器)-C間0.5km、C-D間1.5km、D-A間2.0kmである。
ただし、電線1線当たりの抵抗は0.2Ω/kmとし、リアクタンスは無視するものとして、次の(a)及び(b)の問に答えよ。
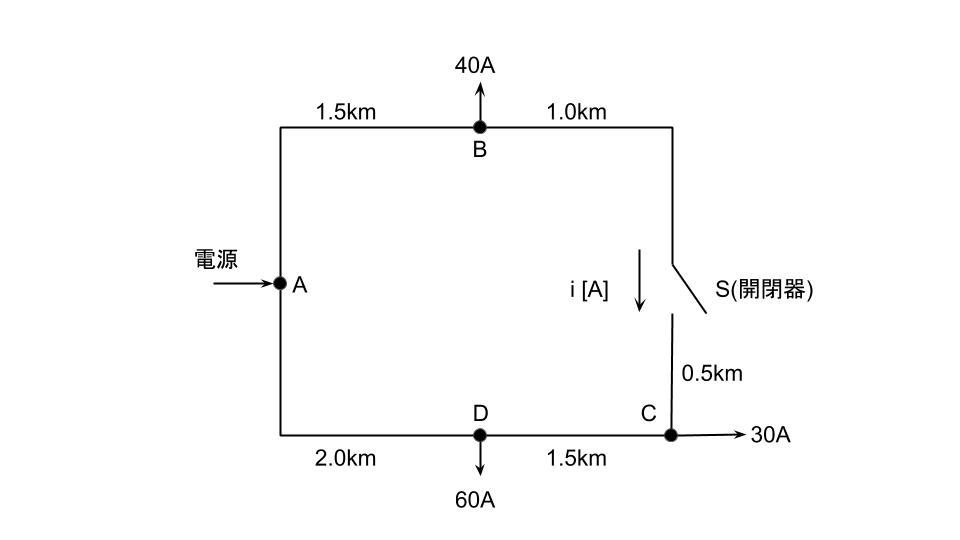
(a)電源A点から見たC点の電圧降下の値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、電圧は相間電圧とする。
| (1)41.6 | (2)45.0 | (3)57.2 | (4)77.9 | (5)90.0 |
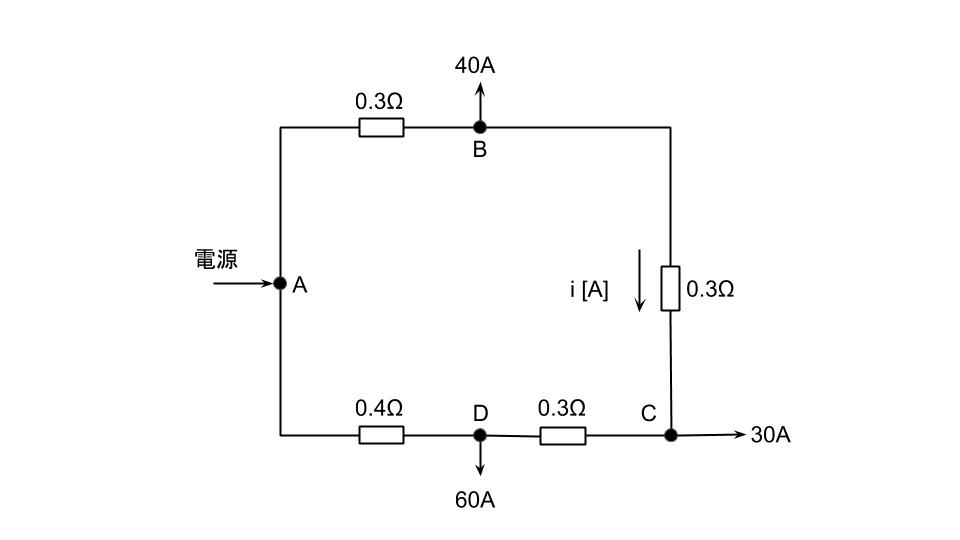
(b)開閉器Sを投入した場合、開閉器Sを流れる電流iの値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
| (1)20.0 | (2)25.4 | (3)27.5 | (4)43.8 | (5)65.4 |

 https://archivelog.net/denken/
https://archivelog.net/denken/
ディスカッション
コメント一覧
まだ、コメントがありません