電験３種過去問【2012年電力 問13】

解答 

（３）

解説

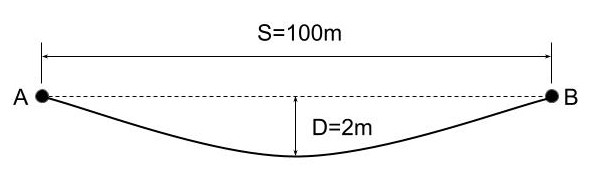
電線の実長L[m]は次式で求められる。ここで、電線のたるみD[m]、電線の径間S[m]。

\(\displaystyle L=S+\frac{8D^2}{3S}\)

電線の実長L[m]のとき、温度変化による電線長L’[m]は、１[℃]あたりの線膨張係数をα、温度差をt[℃]とすると

\(\displaystyle L’=L(1+αt)\)

題意より、導体の温度が30[℃]のとき、たるみD=2[m]なので、電線の実長L[m]は

\(\displaystyle L=S+\frac{8D^2}{3S}=100+\frac{8\times2^2}{3\times100}=100.10667\)

導体の温度が60[℃]のになったとき、電線の実長L’[m]は（温度差t=30℃）

\(\displaystyle L’=L(1+αt)=100.10667(1+1.5\times10^{-5}\times30)=100.15172\)

したがって、導体の温度が60[℃]のになったときの、たるみD'[m]は

\(\displaystyle L’=S+\frac{8D’^2}{3S}\)

\(\displaystyle 100.15172=100+\frac{8\times D’^2}{3\times100}\)

\(\displaystyle D’=\sqrt{\frac{300(100.15172-100)}{8}}=2.39\)

60[℃]での電線のたるみは2.39[m]となる。