電験1種過去問【2015年電力管理 問1】
【水力発電】水車の比速度の導出《計算問題》
ランナの直径 D₁ が 0.4 m のフランシス水車で、有効落差 H₁ が 1m のとき、水車出力 P₁ が 1 kW、使用水量 Q₁ が 0.121 m³/s、回転数 N₁ 149.5 rpm のモデル水車(以下水車 A と呼ぶ。)がある。
この水車 A と相似な水車(以下水車 B と呼ぶ。)を、有効落差 H₂ が 121m のとき、使用水量 Q₂ が 10 m³/s の条件の場所に設置したい。次の問に答えよ。
ただし、水車効率 η [%] は水車 A、水車 B で同一とし、水車 B のランナの直径を D₂ [m] 、相似比を k (k=\(\frac{D_2}{D_1}\)) とする。また、重力加速度 g は 9.8 m/s² 、水の密度 ρ は 1 000 kg/m³ とする。
(1)水車 B の出力 P₂ [kW] を求めよ。
(2)水車 B の使用水量 Q₂ [m³/s] を Q₁ , H₁ , H₂ 及び k を用いて表せ。
(3)水車 B の出力 P₂ [kW] を P₁ , H₁ , H₂ 及び k を用いて表せ。
(4)水車 B のランナ直径 D₂ [m] を求めよ。
(5)水車 B の回転数 N₂ [rpm] を N₁ , H₁ , H₂ , P₁ 及び P₂ を用いて表し、その値を求めよ。
追加学習は水力発電の学習帳で
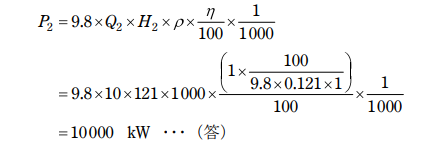
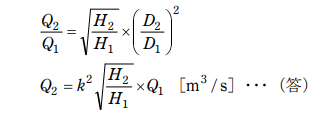
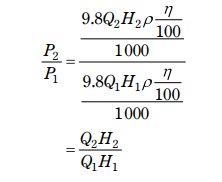
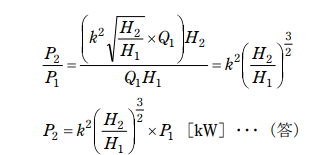
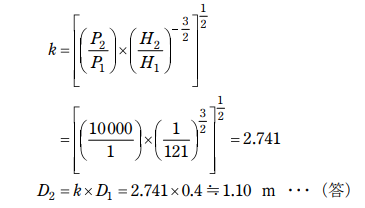
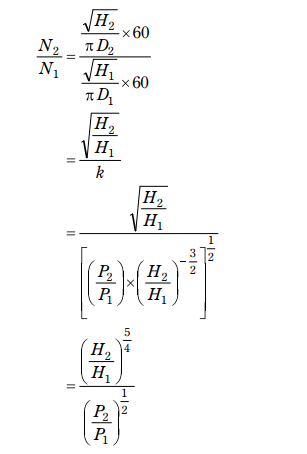
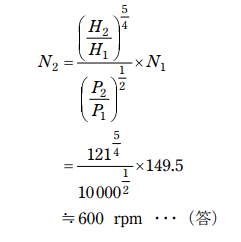

ディスカッション
コメント一覧
まだ、コメントがありません