電験１種過去問【2017年電力管理 問4】

解答

公式標準解答

(1) 故障点抵抗が零で，かつ，故障点までの直列抵抗も零であるから，短絡発生後の発電機出力は零である。発電機の固定子抵抗が零なので電気的トルクも短絡発生とともにステップ的に零となる。一方，故障発生前は定格出力運転であるため，電気的トルクは0.9p.u.である。したがって，短絡時のステップ変化の大きさは，
0.9-0.0=0.9p.u. ･･･（答）

(2) 調速機の効果は無視するため，故障中の機械的入力 P_m は故障前から変化しない。故障前は一定速度で運転していたのだから，P_m は電気的出力 P_e とバランスしており，その大きさは 0.9 p.u. である。一方，故障中の電気出力は零を保つ。したがって，故障中の発電機の運動方程式は以下のとおりである。

(5) 再閉路時に故障点の短絡が解消されていない場合に，再閉路が行われると再び三相短絡が発生し，(1)で求めたような大きな電気的トルクが再び軸に加わることになる。このため軸は故障発生時に加速方向，故障除去時に減速方向，再閉路(失敗)時に再び加速方向の電気的トルクの急激な変化にさらされる。この大きな衝撃によって軸にはねじれ振動が発生するが，その減衰は一般に極めて悪く，固有振動数は 10 Hz 程度である。このため，再閉路失敗のタイミングが 0.1 秒程度以下の範囲で僅かに前後するだけで，その瞬間の軸のねじれ振動は様々な状態をとりうる。最悪の場合としては軸がちょうど加速しているところで再閉路失敗の加速方向のステップ変化を受けることも考えられ，この場合には軸は大きく機械的に歪むことになり，材料疲労は過酷となる。

解説

（2）\(\frac{dω}{dt}\)=0.12857 [p.u.] の両辺を t で積分すると
　ω=0.12857t
　Δδはωをt=0→0.1秒の期間で積分したものであるので
　Δδ=0.12857×\(\left[\frac{1}{2}t^2\right]_0^{0.1}\) [p.u]
　　=0.00064285 [p.u.]
∴Δδ=0.00064285×2πf [rad]
　　=0.20195 [rad]

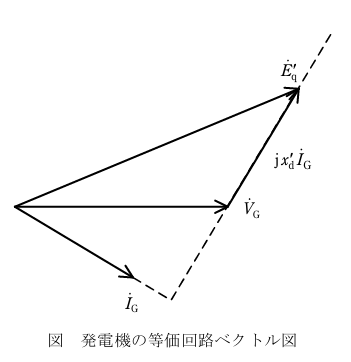
（3）発電機出力端の電圧をV、電流をI_G、送電電力を P + jQ とすると、
　P+ jQ = V\(\bar{\dot{I_G}}\)
　0.9+j0.43589=1.0×\(\bar{\dot{I_G}}\)
　\(\dot{I_G}\)=0.9-j0.43589[p.u.]

　高速再閉路時の発電機タービンに与える影響に関する問題です。かなり専門的な内容であり、初見で解くのは困難です。一度でも類題に触れたことがあればかなり難易度が下がったかもしれませんが、そのような方は多くないと思います。しかし、電験試験の本丸を攻めた問題であるので、今後も類題が出題される可能性は低くないと思います。しっかり理解しておきたいところです。

難易度５（★★★★★）