情報処理の学習帳
マイクロプロセッサの動作クロック
図はマイクロプロセッサの動作クロックを示す。
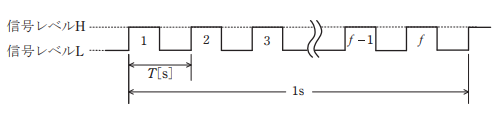
マイクロプロセッサは動作クロックと呼ばれるパルス信号に同期して処理を行う。1クロックの周期 T [s] をサイクルタイム、1秒当たりの動作クロック数 f [Hz]を動作周波数と呼ぶ。
\(\displaystyle f=\frac{1}{T}\)[Hz]
また、マイクロプロセッサが1命令当たりに使用する平均クロックを CPI と呼ぶ。1命令当たりの平均実行時間TE[s]と1クロックの周期 T [s] との関係は
\(\displaystyle T=\frac{T_E}{CPI}\)[s]
算術演算
2進数と16進数表現
10進数と2進数及び16進数の対応は以下のようになる。
\(\small{\begin{array}{cccc}
10進数&2進数&16進数&2進数が表す10進数値\\
\hline 0&0000&0&0\times2^3+0\times2^2+0\times2^1+0\times2^0\\
\hline 1&0001&1&0\times2^3+0\times2^2+0\times2^1+1\times2^0\\
\hline 2&0010&2&0\times2^3+0\times2^2+1\times2^1+0\times2^0\\
\hline 3&0011&3&0\times2^3+0\times2^2+1\times2^1+1\times2^0\\
\hline 4&0100&4&0\times2^3+1\times2^2+0\times2^1+0\times2^0\\
\hline 5&0101&5&0\times2^3+1\times2^2+0\times2^1+1\times2^0\\
\hline 6&0110&6&0\times2^3+1\times2^2+1\times2^1+0\times2^0\\
\hline 7&0111&7&0\times2^3+1\times2^2+1\times2^1+1\times2^0\\
\hline 8&1000&8&1\times2^3+0\times2^2+0\times2^1+0\times2^0\\
\hline 9&1001&9&1\times2^3+0\times2^2+0\times2^1+1\times2^0\\
\hline 10&1010&A&1\times2^3+0\times2^2+1\times2^1+0\times2^0\\
\hline 11&1011&B&1\times2^3+0\times2^2+1\times2^1+1\times2^0\\
\hline 12&1100&C&1\times2^3+1\times2^2+0\times2^1+0\times2^0\\
\hline 13&1101&D&1\times2^3+1\times2^2+0\times2^1+1\times2^0\\
\hline 14&1110&E&1\times2^3+1\times2^2+1\times2^1+0\times2^0\\
\hline 15&1111&F&1\times2^3+1\times2^2+1\times2^1+1\times2^0\\
\hline\end{array}}\)
2進数の4ビットごとに16進数の桁上がりとなることから、2進数を16進数に変換するには、2進数4ビットごとに区切って16進数に変換すればよい。
<例>
2進数の(111011)2を変換すると、
以下のように16進数の(3B)16になる。
\(\small{\begin{array}{cccc}
&&&計算方法\\
\hline 2進数&0011&1011&4ビットで区切る\\
\hline 10進数(過程)&3&11&各区切りの10進数値\\
\hline 16進数&3&B&各区切りの16進数値\\
\hline\end{array}}\)
過去問題:
電験3種過去問【2021年機械 問14】(2,10,16進数表現)
真理値表と論理式
フリップフロップ回路
コンピュータ内の処理では、入力の順序に依存して出力が決まる必要がある。入力の順序を記憶しておくための回路を一般に順序回路と呼ぶ。順序回路の記憶を行うのがフリップフロップ回路である。これらはカウンタ回路やレジスタ回路などとして用いられる。
RSフリップフロップ回路
RSフリップフロップ回路においては、入力RとSがそれぞれ1と0の場合に0(リセット)を、入力RとSがそれぞれ0と1の場合に1(セット)を出力する。入力RとSが共に0では出力状態を保持し、入力RとSを共に1とすることは禁止されている。
\(\small{\begin{array}{|cc|c|c|}
\hline 入力&&出力&状態\\
S^n&R^n&Q^{n+1}&\\
\hline 0&0&Q^{n}&記憶\\
\hline 0&1&0&リセット\\
\hline 1&0&1&セット\\
\hline 1&1&禁止&禁止\\
\hline\end{array}}\)
JKフリップフロップ回路
JKフリップフロップ回路は、RSフリップフロップ回路のS=J、R=Kとしたもので、J=K=1(RSフリップフロップでは禁止)の場合に、フリップフロップの出力を反転するようにしたもの。この回路は最もよく使われている。
入力JとKがそれぞれ1と0の場合に1(セット)を、入力JとKがそれぞれ0と1の場合に0(リセット)を出力し、入力JとKが共に0では出力状態を保持し、入力JとKを共に1では出力を反転する。
\(\small{\begin{array}{|cc|c|c|}
\hline 入力&&出力&状態\\
J&K&Q^{n+1}&\\
\hline 0&0&Q^n&記憶\\
\hline 0&1&0&リセット\\
\hline 1&0&1&セット\\
\hline 1&1&\bar{Q^n}&反転\\
\hline\end{array}}\)
Dフリップフロップ回路
RSフリップフロップ回路にR=S=1が禁止されている。D(Deley)フリップフロップ回路は、D=1ではS=1,R=0(セット)を、D=0ではS=0,R=1(リセット)をRSフリップフロップ回路へ入力するようにしたもの。
Dフリップフロップ回路は、入力Dの状態を1クロック遅れ(Delay)させている。
\(\small{\begin{array}{|cc|c|c|}
\hline 入力&&出力&状態\\
D^n&Q^n&Q^{n+1}&\\
\hline 0&0&0&リセット\\
\hline 0&1&0&リセット\\
\hline 1&0&1&セット\\
\hline 1&1&1&セット\\
\hline\end{array}}\)
\(\small{\begin{array}{|c|c|}
\hline 入力&出力\\
D^n&Q^{n+1}\\
\hline 0&0\\
\hline 1&1\\
\hline\end{array}}\)
Tフリップフロップ回路
T(Toggles:トグル)フリップフロップ回路は、入力T=1のとき出力Qの状態を切り替える(トグル)機能がある。T=0ではQの状態は変化しない。
TフリップフロップはJKフリップフロップから容易につくることができるため、TフリップフロップのICはない。
\(\small{\begin{array}{|cc|c|c|}
\hline 入力&&出力&状態\\
T&Q^n&Q^{n+1}&\\
\hline 0&0&0&記憶\\
\hline 0&1&1&記憶\\
\hline 1&0&1&反転\\
\hline 1&1&0&反転\\
\hline\end{array}}\)
\(\small{\begin{array}{|c|c|}
\hline 入力&出力\\
T&Q^{n+1}\\
\hline 0&Q^n\\
\hline 1&\bar{Q^n}\\
\hline\end{array}}\)
Tフリップフロップ回路は多段結合して、カウンタなどの用途に使用される。
以下に16進カウンタの例を示す。
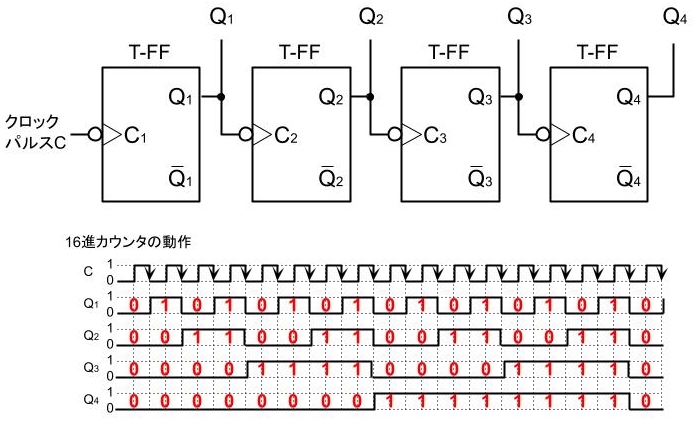
クロックパルスCの立下りで、Q1は状態変化する。また、Q1の立下りでQ2も状態変化する。 これを繰り返し動作することで、Q1はCの2倍の周期、Q2はQ1の2倍の周期、Q3はQ2の2倍の周期、Q4はQ3の2倍の周期となる。
Q1、Q2、Q3、Q4の組合せを、クロックパルスごとに0~15までカウントするカウンタとして用いることができる。
\(\small{\begin{array}{|cccc|c|}
\hline Q_4&Q_3&Q_2&Q_1&10進数\\
\hline 0&0&0&0&0\\
\hline 0&0&0&1&1\\
\hline 0&0&1&0&2\\
\hline 0&0&1&1&3\\
\hline 0&1&0&0&4\\
\hline 0&1&0&1&5\\
\hline 0&1&1&0&6\\
\hline 0&1&1&1&7\\
\hline 1&0&0&0&8\\
\hline 1&0&0&1&9\\
\hline 1&0&1&0&10\\
\hline 1&0&1&1&11\\
\hline 1&1&0&0&12\\
\hline 1&1&0&1&13\\
\hline 1&1&1&0&14\\
\hline 1&1&1&1&15\\
\hline 0&0&1&1&3\\\hline\end{array}}\)
過去問題:
電験3種過去問【2021年機械 問18】(フリップフロップ回路の知識)
A/Dコンバータ
標本化と量子化
アナログ信号をコンピュータで利用するには、A-D変換によりディジタル信号に変換する必要がある。
連続したアナログ信号を適当な時間間隔で区切り、断続的な信号とすることを標本化という。標本化定理によると、入力信号を完全に復元するためには、その入力信号に含まれる最高周波数成分の2倍を超えたサンプリングレートとすればよい。
標本化されたアナログ値を飛び飛びの不連続な値で表すことを量子化という。量子化の段階数が増え、量子化の単位が小さくなるほど、量子化誤差は小さくなる。
A-D変換器には主に次のような方式がある。
積分形
積分形には、入力信号を一定時間積分し、この積分結果と一定の基準信号を積分した値が等しくなる時間を計測し、この計測値から変換結果を得る方式がある。サンプリングレートは低いが、高精度でノイズに強い方式である。
逐次比較形
逐次比較形には、入力信号と内部のD-A変換器の出力を2分検索で比較していき、ディジタル値に変換する方式がある。nビットの変換には、MSB側からn回の比較が必要なため、中程度のサンプリングレートとなる。変換精度を得るために、サンプリングホールド回路により、標本化される信号レベルが変換終了まで変動しないようにする場合がある。
並列形
並列形はフラッシュ形とも称され、nビットの変換には(2n-1)個の基準電圧と比較器を準備し、入力信号をそれらで同時に比較して変換する方式がある。高いサンプリングレートを得られるが、回路規模は大きくなる。
過去問題:
電験2種過去問【2021年機械 問8】(AD変換器の方式)
プログラム
フローチャート
フローチャートは、プロセスの各ステップを箱で表し、その流れをそれらの箱の間の矢印で表すことで、プロセスを表現する図である。
プログラム言語の構成
マイクロコンピュータのプログラム命令は、メモリから命令レジスタに読み込まれた後、命令デコーダで解読されて制御回路へ伝達される。このようなマイクロコンピュータが直接理解できるプログラム命令は、2進数で記述された機械語である。機械語を扱うときには、2進数4桁分を表す16進数を用いることが多い。
一般的に機械語命令は、基本動作を表す命令コードと命令の対象となる数値やデータのアドレスなどを表現するオペランドによって構成される。例えば、相対アドレスを指定する場合は、プログラムカウンタの値にオペランドによって指定した値を加えて、目的のアドレスを算出する。停止命令や無操作命令など、一部の命令ではオペランドの無い命令もある。
アセンブラは、機械語とほぼ、1対1に対応したニモニックを用いる言語で、機械語よりもプログラム内容が分かりやすい。
機械語やアセンブラを低水準言語という。
人間が理解しやすいように記述した原始プログラムを一括して機械語などの低水準言語に変換する言語を総称して、コンパイラ言語という。この変換作業によって原始プログラムは目的プログラムとなり、さらに別の目的プログラムやライブラリと結合させて実行可能プログラムとなる。
実行時に原始プログラムを一文ずつ解釈し、逐次実行していく言語としてインタプリタ言語がある。この言語は、コンパイラ言語に対してプログラム変更手順が容易であるが、実行速度は遅くなる。
オペレーティングシステム
オペレーティングシステムは、複数のタスクに対して、優先度に基づきCPUやメモリ、通信インターフェースなどのハードウェア資源を効率的に割り当て、システム全体の遊び時間を少なくすることで\(\fbox{スループット}\)を高めている。このように、タスクを管理して、ハードウェア資源を有効活用する機能をタスク管理という。
タスクは生成されると、\(\fbox{実行可能}\)状態となる。実行状態にあるタスクからCPUの占有が解かれると、タスクディスパッチャが\(\fbox{実行可能}\)状態にあるタスクの中から最も優先度の高いタスクにCPUの使用権を与え、実行状態に移行させる。
複数のタスクを切替えて実行する場合、タスクの切替えタイミングが重要となる。一例として、外部や内部の\(\fbox{割込み}\)により発生する状態変化のタイミングを用いるイベントドリブン方式がある。
タスクの実行順序は、\(\fbox{FIFO}\)(First In, First Out)と呼ばれる構造の待ち行列にタスクを格納して処理を行う到着順方式や、処理時間の短いタスクを最初に実行する処理時間順方式がある。その他に、あらかじめタスク優先度を付与しておき、優先順位に従って処理する方式がある。しかしこの方式では、優先度の\(\fbox{低い}\)タスクが実行されないスタベーションと呼ばれる現象が起こる可能性があり、動的に優先度を変更する対策などが行われる。
プログラムテスト法
ソフトウェア開発には、いくつかのプロセスモデルがある。要求定義、設計、実装(プログラミング)、テストなどの工程を上流工程から下流工程へ\(\fbox{逐次的}\)に遂行していくウォータフォールモデルにおいて、開発者のプログラムテストは、システムの最も小さな構成単位であるモジュールの単体テストから開始し、\(\fbox{結合}\)テスト、システムテストへとボトムアップ的に行う。しかしこの進め方においては、最上流の要求定義に起因する欠陥が、最後のシステムテストの段階にならないという構造的問題がある。この開発リスクを回避するために、現在では比較的短時間で分析や設計、評価を繰り返し行う反復的なプロセスモデルも用いられている。
テスト工程では、静的解析ツールを用いたプログラム構造解析も行われるが、実行による正しさを確認するためには、実際にソフトウェアを実行環境で動作させる必要がある。単体テストの場面では、プログラムの一部モジュールだけを実行可能なようにテスト環境を整えなければならないため、本来のプログラムに代わって、被テストモジュールを模擬的に呼び出す\(\fbox{ドライバ}\)や被テストモジュールから呼び出され模擬的な応答をするスタブを準備することが行われる。
テストを網羅的に行うためには、初めの段階ではプログラムの内部構造に基づいてテスト項目を選ぶ方法で行われる。その後、\(\fbox{結合}\)テスト、システムテストと進み、対象のプログラム量が\(\fbox{大きくなる}\)に従って、内部構造には関知せずに、インターフェースの仕様からテスト項目を選ぶ\(\fbox{ブラックボックス}\)テストの比重が大きくなる。
バブルソート
バブルソートは、ふたつの配列の値を比較して条件に応じた交換を行う整列アルゴリズム。「値の大きい順(降順)」か「値の小さい順(昇順)」に配列を並び替える。
このソートを実行すると条件に応じた要素が泡のように浮かびあがってくるように見えるため、バブル(bubble: 泡)ソートと呼ばれる。
電子機械の構成と基礎技術
ディジタルカメラや自動洗濯機など我々が日常で使う機器、ロボット、生産工場の工作機械など、多くの電子機械はメカトロニクス技術によって設計・製造され、運用されている。機械にマイクロコンピュータを取り入れるようになり、メカトロニクス技術は発展してきた。
電子機械では、外界の情報や機械内部の運動状態を各種センサにより取得する。大部分のセンサ出力は電圧または電流の信号であり時間的に連続に変化する(ア)アナログ信号である。電気、油圧、空気圧などのエネルギーを機械的な動きに変換するアクチュエータも(ア)アナログ信号で動作するものが多い。これらの信号波コンピュータで構成される制御機器で(イ)ディジタル信号として処理するため、信号の変換器が必要となる。(ア)アナログ信号から(イ)ディジタル信号への変換器を(ウ)A-D変換器、その逆の変換器を(エ)D-A変換器という。センサの出力信号波は(ウ)A-D変換器を介してコンピュータに取り込まれ、コンピュータで生成されたアクチュエータへの指令は(エ)D-A変換器を介してアクチュエータに送られる。その間必要に応じて信号レベルを変換する。このような、センサやアクチュエータとコンピュータの橋渡しの機能をもつものを(オ)インタフェースという。
メカトロニクスとその構成要素
メカトロニクスは(ア) 機械技術、(イ) 電子技術、情報技術を統合した技術である。これにより、メカニズム(機構)によってつくられた従来の(ア) 機械に、マイクロコンピュータなどの(イ) 電子部品を組み込んで、高性能で多機能な機械装置が実現できる。
メカトロニクス製品の構成要素には、(ウ) センサ、(エ) アクチュエータ、(オ) コンピュータ及びインターフェースがある。(ウ) センサは、機械の圧力、力、速度、加速度、温度などの物理量を計測する。(エ) アクチュエータは、電気、油圧、空気圧などのエネルギーを機械的な動きに変換する。(オ) コンピュータは、(ウ) センサで計測した情報を処理して(エ) アクチュエータへの指令を生成する制御装置としての役割を果たす。インターフェースは、(ウ) センサや(エ) アクチュエータの扱う電気信号と(オ) コンピュータが処理できるディジタル信号との変換を担当する。
産業用自動制御機器
予め定められた順序又は手続きに従って、制御の各段階を逐次進めていく制御方式をシーケンス制御と言い、各種産業の自動機で用いられている。
旧来は、状態記憶を利用した順序回路である自己保持回路などで制御を実現していたが、現在では、専用の工業用制御機器であるプログラマブルロジックコントローラを用いるのが主流である。この機器はプログラムにより動作するため、複雑な理論を実現できることや配線の変更なしに機能変更ができる利点を持つ。
プログラマブルロジックコントローラの入力側には操作ボタンや各種センサなどが接続され、出力側には表示灯や各種アクチュエータなどが接続される。この機器は、一般的なパーソナルコンピュータよりも信頼性に優れることにより、産業現場の過酷な環境においても活用されている。
プログラムは、旧来のリレー回路をはしご状に接続する表現としたラダー図の図式により記述されることもあるが、現在では、広範な用途に対応できるよう、各種プログラム記述方法が準備されている。
産業用自動機の中核として用いられるプログラマブルロジックコントローラが故障した場合でも、安全な状態に移行するようフェールセーフに配慮した装置設計が求められている。
電気通信
文字や音声、画像などの情報を電気信号や光信号に変換してやりとりすることを電気通信といい、様々な用途や場所で利用されている。
- 通信には、通信ケーブルを伝送路として用いる有線通信と、空間を伝送路として用いる無線通信がある。通信の用途に応じて適切な方式が選択される。
- 電気信号に変換した情報を扱う方式として、アナログ方式とディジタル方式がある。アナログ方式は古くから使用されてきたが、ディジタル方式は、雑音(ノイズ)の影響を受けにくいことや、小型化しやすいこと、コンピュータで処理しやすいことなどから、近年では採用されることが多くなっている。
- 光通信の伝送路として主に用いられる光ファイバケーブルでは、入射した光信号は屈折率の異なるコアとクラッドの間で全反射しながら進んでいく。光ファイバケーブルは伝送損失が非常に少なく、無誘導のため漏話しにくいことから、長距離の伝送に適している。
- 無線通信に用いられる電波の伝わり方は、周波数や波長によって異なるために、通信の用途にあったものが用いられる。周波数の高い、すなわち波長の短い電波は直進性が強いために、特定の方向に向けて発信するのに適している。
- データ通信における誤りの検出方法としてよく使用されるパリティチェック方式は、伝送データのビット列に対して、状態が”1”のビットの個数が奇数または偶数になるように、検査のためのビットを付け加えて送ることで、受信側で誤りを検出する方式である。
電気通信において、信号に変換された情報を伝える媒体を伝送路と呼ぶ。伝送路などから混入し、送りたい信号を変化させてしまうことがある不要な成分を(ア)雑音(ノイズ)という。
身近な通信手段の一つとして電話がある。地域間をまたがる電話網において多数の通話を効率的に中継するために、1本の伝送路を用いて同時に多数の通話を伝送する技術を(イ)多重化という。
無線通信では、送りたい情報を信号波と呼ばれる電気信号に変換した後、送信機によって、周波数のより高い搬送波と呼ばれる信号と合成し、(ウ) 変調波を作る。(ウ) 変調波を作り出したり、受信機において(ウ) 変調波から信号波を取り出す方式はいくつかある。
アナログ信号をディジタル信号に変換するA-D変換においては、アナログ信号の最高周波数に対して、その2倍以上の周波数で(エ) 標本化を行えば、(エ) 標本化された信号から元のアナログ信号を再現できる。これを(エ) 標本化定理という。
画像や音声、ビデオなどの情報をそのまま記録・伝送しようとすると、データのサイズが大きくなるために、データの(オ) 圧縮が行われる。静止画像の代表的な(オ) 圧縮方法としてJPEGという国際標準規格がある。
ネットワーク通信
ネットワーク内には、端末となるコンピュータの他に、通信回線を延長したり制御したりするための各種中継機器が用いられている。
\(\fbox{リピータ}\)は、伝送路で減衰した信号を増幅、補正して、さらに遠方まで伝送するための機器で、OSI参照モデルの物理層の中継を行う。この機器は、信号の解釈をするものではなく、アドレスを参照した制御機能をもたない。
\(\fbox{ブリッジ}\)は、複数のLANを接続する機器であり、OSI参照モデルのデータリンク層の中継を行う。この機器は、\(\fbox{MAC}\)アドレスによってネットワークを制御する。代表的な機器としてスイッチングハブがある。
物理層とデータリンク層の一部を定義したIEEE 802.11関連規格があり、これに対応した無線中継機器を利用することで、\(\fbox{Wi-Fi}\)によるLANへの無線接続ができる。
ルータは、\(\fbox{ブリッジ}\)と同様に複数のLANを接続する機器であり、OSI参照モデルのネットワーク層での中継を行う。この階層で用いるアドレスは\(\fbox{DHCP}\)サーバを用いることで自動的にクライアントへ割り当てられるため、利用者はコンピュータをネットワークに接続しただけで通信環境を整えることができる。

ディスカッション
コメント一覧
まだ、コメントがありません