電験３種過去問【2021年理論 問17】

解答

（a）：（４）
（b）：（２）

解説

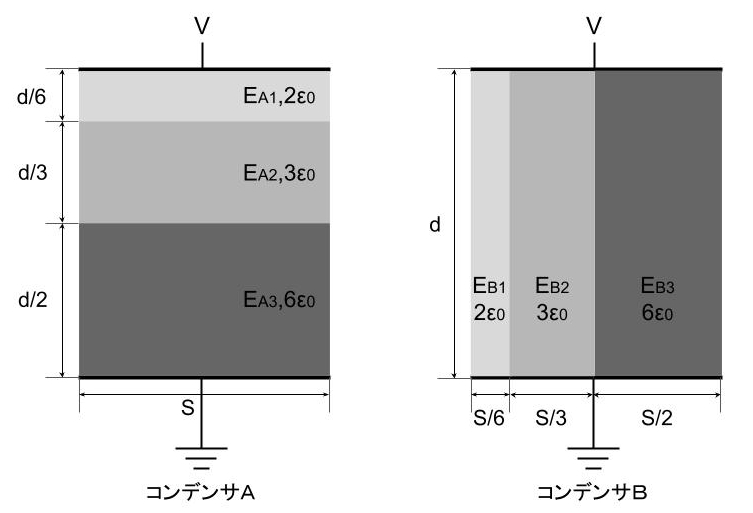
（a）コンデンサAにおいて、極板間の磁束密度D[C/m²]は各誘電体内部で等しいので、

$\displaystyle D=2ε_0 E_{A1}=3ε_0 E_{A2}=6ε_0 E_{A3}\text{[C/㎡]}$

$\displaystyle ∴E_{A1}=\frac{3}{2}E_{A2}=3E_{A3}$

$\displaystyle E_{A1}$を基準とすると、

$\displaystyle E_{A2}=\frac{2}{3}E_{A1}$

$\displaystyle E_{A3}=\frac{1}{3}E_{A1}$

上式の関係から、E_A1が一番大きく、E_A2は2番目に大きく、E_A3が一番小さい。

電圧V[V]は「電界の強さ×距離」であるので、

$\displaystyle V=\frac{d}{6}E_{A1}+\frac{d}{3}E_{A2}+\frac{d}{2}E_{A3}$

$\displaystyle =\frac{d}{6}E_{A1}+\frac{d}{3}\left(\frac{2}{3}E_{A1}\right)+\frac{d}{2}\left(\frac{1}{3}E_{A1}\right)$

$\displaystyle =\frac{d}{6}E_{A1}+\frac{2d}{9}E_{A1}+\frac{d}{6}E_{A1}$

$\displaystyle =\frac{3d}{18}E_{A1}+\frac{4d}{18}E_{A1}+\frac{3d}{18}E_{A1}$

$\displaystyle =\frac{10d}{18}E_{A1}$

$\displaystyle ∴V=\frac{5d}{9}E_{A1}$

$\displaystyle ∴E_{A1}=\frac{9V}{5d}$

（b）静電容量C[F]のコンデンサに、電位差V[V]が与えられているとき、蓄えられるエネルギーW[J]は

$\displaystyle W=\frac{1}{2}CV^2\text{[J]}$

コンデンサの静電容量C[F]は

$\displaystyle C=ε\frac{S}{d}\text{[F]}$

となる。

コンデンサAは、各誘電体のコンデンサ$\displaystyle C_{A1}、C_{A2}、C_{A3}$が直列に接続されていると考えると、

$\displaystyle C_{A1}=2ε_0\frac{S}{\left(\frac{d}{6}\right)}=12ε_0\frac{S}{d}\text{[F]}$

$\displaystyle C_{A2}=3ε_0\frac{S}{\left(\frac{d}{3}\right)}=9ε_0\frac{S}{d}\text{[F]}$

$\displaystyle C_{A3}=6ε_0\frac{S}{\left(\frac{d}{2}\right)}=12ε_0\frac{S}{d}\text{[F]}$

$\displaystyle C_{A1}、C_{A2}、C_{A3}$が直列に接続されているときの合成静電容量$\displaystyle C_{A}$は、次式となる。

$\displaystyle C_{A}=\frac{C_{A1}C_{A2}C_{A3}}{C_{A1}C_{A2}+C_{A2}C_{A3}+C_{A1}C_{A3}}\text{[F]}$

$\displaystyle K=ε_0\frac{S}{d}$とおくと、

$\displaystyle C_{A}=\frac{1296K^3}{108K^2+108K^2+144K^2}$

$\displaystyle =\frac{1296K^3}{360K^2}$

$\displaystyle =3.6K\text{[F]}$

コンデンサBは、各誘電体のコンデンサ$\displaystyle C_{B1}、C_{B2}、C_{B3}$が並列に接続されていると考えると、

$\displaystyle C_{B1}=2ε_0\frac{\left(\frac{S}{6}\right)}{d}=\frac{1}{3}ε_0\frac{S}{d}\text{[F]}$

$\displaystyle C_{B2}=3ε_0\frac{\left(\frac{S}{3}\right)}{d}=ε_0\frac{S}{d}\text{[F]}$

$\displaystyle C_{B3}=6ε_0\frac{\left(\frac{S}{2}\right)}{d}=3ε_0\frac{S}{d}\text{[F]}$

$\displaystyle C_{B1}、C_{B2}、C_{B3}$が並列に接続されているときの合成静電容量$\displaystyle C_{B}$は、次式となる。

$\displaystyle C_{B}=C_{B1}+C_{B2}+C_{B3}\text{[F]}$

$\displaystyle K=ε_0\frac{S}{d}$とおくと、

$\displaystyle C_{B}=\left( \frac{1}{3}+1+3 \right)K$

$\displaystyle =\frac{13}{3}K$

$\displaystyle =4.33K\text{[F]}$

合成静電容量$\displaystyle C_{A}\text{[F]}$のコンデンサAに、蓄えられるエネルギー$\displaystyle W_{A}\text{[J]}$は

$\displaystyle W_A=\frac{1}{2}C_A V^2\text{[J]}$

同様に、合成静電容量$\displaystyle C_{B}\text{[F]}$のコンデンサBに、蓄えられるエネルギー$\displaystyle W_{B}\text{[J]}$は

$\displaystyle W_B=\frac{1}{2}C_B V^2\text{[J]}$

コンデンサAに蓄えられる蓄積エネルギーの、コンデンサBに蓄えられる蓄積エネルギーに対する比は、

$\displaystyle \frac{W_{A}}{W_{B}}=\frac{C_A}{C_B}=\frac{3.6K}{4.33K}=0.83$